BJOI做题记录

终于想起还要做一下历年省选题了2333

然而咕了的还是比做了的多2333

LOJ #2178. 「BJOI2017」机动训练

咕了。

LOJ #2179. 「BJOI2017」树的难题

啥也不会，暴力点分治。

点分治的时候只有相同颜色的链合并到一起的时候会出事。

一开始以为权值非负，于是胡了个假做法……

把边按颜色排序，每次处理一整段的相同颜色，分两棵线段树维护其他颜色/当前颜色的最大权值，然后就没了。

单调队列神仙做法不会……

代码

LOJ #2180. 「BJOI2017」魔法咒语

L小的时候暴力，大的时候矩阵快速幂。

代码咕了。

LOJ #2492. 「BJOI2018」二进制

仔细分析，发现只有当

只有一个1，若干个0。
奇数个1且没有0。
奇数个1且只有一个0。

的时候不合法。

对于第一种，在1处统计。

对于第二种，对每一段连续的1统计。

对于第三种，在0处统计。

以上纯属口胡，因为代码咕了。

LOJ #2511. 「BJOI2018」双人猜数游戏

咕了。

LOJ #2493. 「BJOI2018」染色

首先不是二分图的东西肯定可以被搞掉。

然后样例已经给了我们一种叉二分图的方法。总结一下就是：用一个环可以强制某个节点选某种颜色。

于是我们可以发现如果一个连通块内有两个不相交的环那么一定会被叉掉。

然后如果连通块内\(m\le n\)，那么显然不能被叉掉。

然后如果一个连通块内\(m\ge n+2\)，那么有一种把它叉掉的方法：

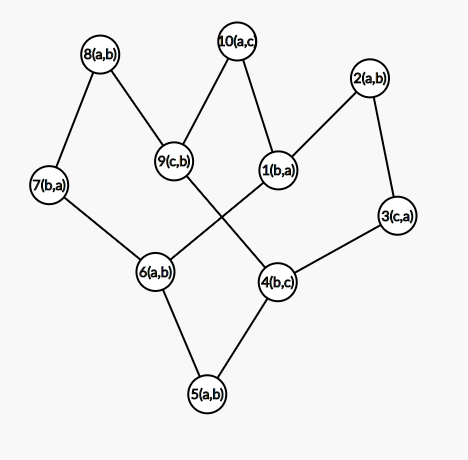
于是就只剩\(m=n+1\)的情况了。此时可以抽象成两个度数为3的点，它们之间有三条路径。

手画一下可以发现长度\((1,3,3),(2,4,4)\)的时候是可以被叉掉的，而长度更长的时候多半也是可以被叉的。

你发现别的都不怎么能被叉掉了，而“别的”就只剩\((2,2,偶数)\)了，就做完了。

LOJ #2491. 「BJOI2018」求和

树上差分。

LOJ #2513. 「BJOI2018」治疗之雨

预处理出一轮之后掉\(i\)点血的概率，\(i\in [-1,n]\)。

设\(dp_i\)表示\(i\)滴血时期望轮数，于是这只会和\([0,i+1]\)的\(dp\)值有关。

于是\(O(n^2)\)推出\(dp_n=k_1\times dp_1+b_1=k_2\times dp_1+b_2\)之后解方程即可。

代码咕了。

LOJ #2512. 「BJOI2018」链上二次求和

设\(S_i\)表示原序列前缀和，\(SS_i\)表示前缀和的前缀和。
\[
\begin{align*}
ans&=\sum_{i=l}^r \sum_{j=i}^n (S_j-S_{j-i})\\
&=(r-l+1)SS_n-\sum_{i=l-1}^{r-1} SS_i-\sum_{i=n-r}^{n-l}SS_i
\end{align*}
\]
问题转化为维护\(SS_i\)，显然可以线段树。

LOJ #3093. 「BJOI2019」光线

设\(f_i,g_i\)分别表示从左往右/从右往左打在这块玻璃上，最后到终点的光线。

容易发现这两个只和\(f_{i+1},g_{i-1}\)有关。

于是从右往左递推解方程即可。可能是因为数据随机不会出现解不出的情况。

LOJ #3094. 「BJOI2019」删数

一个结论：对于\(i\)和\(i\)出现的次数\(cnt_i\)，我们把\([i-cnt_i+1,i]\)铺上线段，那么最终答案就是\([1,n]\)没有被铺上的长度。证明显然？

维护\([1,n]\)的0的位置个数，那么单点修改就是单点修改，整体修改就是把\([1,n]\)这个区间左右移动。

代码咕了。

LOJ #3090. 「BJOI2019」勘破神机

对于\(m=2\)，\(f_n\)表示长度为\(n\)的序列的方案数，那么\(f_n\)就是斐波那契数列。

对于\({f_n\choose k}\)，可以用斯特林数把它转化成\(f_n^k\)求前缀和。我们想起（然而我就是想不起）斐波那契数列有通项公式，于是大力二项式展开即可。

对于\(m=3\)，\(f_n\)表示长度为\(2n\)的序列的方案数，那么\(f_n\)就是&%*&%￥&*（……

推一推，\(f_n=f_{n-1}+2\sum_{i=1}^n f_{n-i}\)，差分一下算出\(f_n=4f_{n-1}-f_{n-2}\)。

同样搞出通项公式就没了。

LOJ #3089. 「BJOI2019」奥术神杖

~~如果我没记错的话~~就是分数规划+AC自动机就没了。

LOJ #3092. 「BJOI2019」排兵布阵

对于每一个城堡处理出放\(i\)个兵能获得多少钱，显然有用的是\(O(s)\)的。

然后大力背包即可。由于保证\(\sum a_i\le m\)可以假装复杂度正确？

LOJ #3091. 「BJOI2019」送别

咕了。