用肘方法确定 kmeans 聚类中簇的最佳数量
说明:
KMeans 聚类中的超参数是 K,需要我们指定。K 值一方面可以结合具体业务来确定,另一方面可以通过肘方法来估计。K 参数的最优解是以成本函数最小化为目标,成本函数为各个类畸变程度之和,每个类的畸变程度等于该类重心与其内部成员位置距离的平方和但是平均畸变程度会随着K的增大先减小后增大,所以可以求出最小的平均畸变程度。
1、示例
# 导入相关模块
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt # 创建仿真聚类数据集
X, y = make_blobs(n_samples=150,
n_features=2,
centers=3,
cluster_std=0.5,
shuffle=True,
random_state=0) distortions = []
Ks = range(1, 11) # 为不同的超参数拟合模型
for k in Ks:
km = KMeans(n_clusters=k,
init='k-means++',
n_init=10,
max_iter=300,
n_jobs=-1,
random_state=0) km.fit(X)
distortions.append(km.inertia_) # 保存不同超参数对应模型的聚类偏差 plt.rcParams['font.sans-serif'] = 'SimHei'
plt.figure('百里希文', figfacecolor='lightyellow') # 绘制不同超参 K 对应的离差平方和折线图
plt.plot(Ks, distortions,'bo-', mfc='r')
plt.xlabel('簇中心的个数 k')
plt.ylabel('离差平方和')
plt.title('用肘方法确定 kmeans 聚类中簇的最佳数量') plt.show()
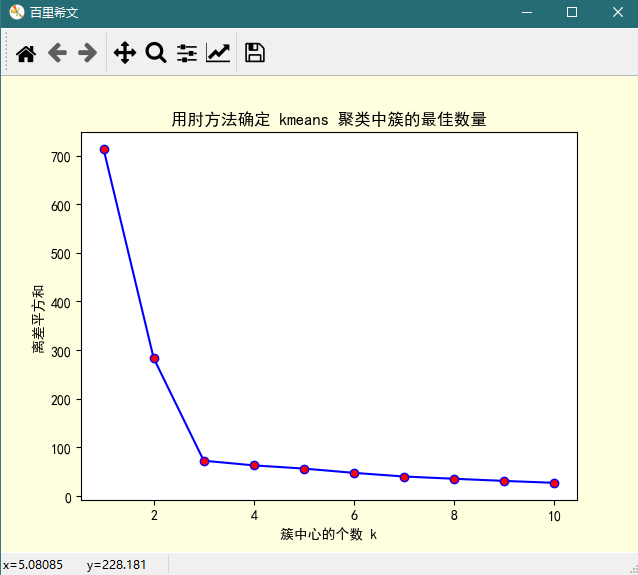
按语:
由上图可知,K 从 1 到 2, 从 2 到 3 的过程中,离差平方和减少的都相当明显,而 K 从 3 到 4,乃至 4 以后,离差平方和减少的都很有限,所以最佳的 K 值应该为 3(与仿真数据集的参数对对应)。由于上图看上去很像一只手肘,理论上最佳的 K 值在肘处取得,故而得名。
2、用平均离差效果似乎更明显
# 导入相关模块
import numpy as np
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
from scipy.spatial.distance import cdist
import matplotlib.pyplot as plt # 创建仿真聚类数据集
X, y = make_blobs(n_samples=150,
n_features=2,
centers=3,
cluster_std=0.5,
shuffle=True,
random_state=0) meanDispersions = []
Ks = range(1, 11) # 为不同的超参数拟合模型
for k in Ks:
km = KMeans(n_clusters=k,
init='k-means++',
n_init=10,
max_iter=300,
n_jobs=-1,
random_state=0) km.fit(X)
meanDispersions.append(sum(
np.min(cdist(X, km.cluster_centers_, 'euclidean'), axis=1))/X.shape[0]) # 保存不同超参数对应模型的聚类偏差 plt.rcParams['font.sans-serif'] = 'SimHei'
plt.figure('百里希文', facecolor='lightyellow') # 绘制不同超参 K 对应的离差平方和折线图
plt.plot(Ks, meanDispersions,'bo-', mfc='r')
plt.xlabel('簇中心的个数 k')
plt.ylabel('平均离差')
plt.title('用肘方法确定 kmeans 聚类中簇的最佳数量') plt.show()
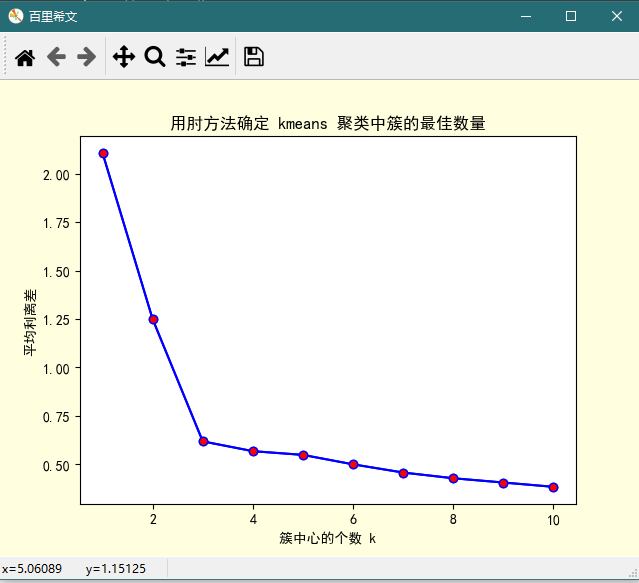
用肘方法确定 kmeans 聚类中簇的最佳数量的更多相关文章
- kmeans聚类中的坑 基于R shiny 可交互的展示
龙君蛋君 2015年5月24日 1.背景介绍 最近公司在用R 建模,老板要求用shiny 展示结果,建模的过程中用到诸如kmean聚类,时间序列分析等方法.由于之前看过一篇讨论kmenas聚类针对某一 ...
- K-Means 聚类
机器学习中的算法主要分为两类,一类是监督学习,监督学习顾名思义就是在学习的过程中有人监督,即对于每一个训练样本,有对应的标记指明它的类型.如识别算法的训练集中猫的图片,在训练之前会人工打上标签,告诉电 ...
- (数据科学学习手札11)K-means聚类法的原理简介&Python与R实现
kmeans法(K均值法)是麦奎因提出的,这种算法的基本思想是将每一个样本分配给最靠近中心(均值)的类中,具体的算法至少包括以下三个步骤: 1.将所有的样品分成k个初始类: 2.通过欧氏距离将某个样品 ...
- Matlab中K-means聚类算法的使用(K-均值聚类)
K-means聚类算法采用的是将N*P的矩阵X划分为K个类,使得类内对象之间的距离最大,而类之间的距离最小. 使用方法:Idx=Kmeans(X,K)[Idx,C]=Kmeans(X,K) [Idx, ...
- k-means+python︱scikit-learn中的KMeans聚类实现( + MiniBatchKMeans)
来源:, init='k-means++', n_init=10, max_iter=300, tol=0.0001, precompute_distances='auto', verbose=0, ...
- 机器学习中K-means聚类算法原理及C语言实现
本人以前主要focus在传统音频的软件开发,接触到的算法主要是音频信号处理相关的,如各种编解码算法和回声消除算法等.最近切到语音识别上,接触到的算法就变成了各种机器学习算法,如GMM等.K-means ...
- Spark MLlib中KMeans聚类算法的解析和应用
聚类算法是机器学习中的一种无监督学习算法,它在数据科学领域应用场景很广泛,比如基于用户购买行为.兴趣等来构建推荐系统. 核心思想可以理解为,在给定的数据集中(数据集中的每个元素有可被观察的n个属性), ...
- 机器学习方法(七):Kmeans聚类K值如何选,以及数据重抽样方法Bootstrapping
欢迎转载,转载请注明:本文出自Bin的专栏blog.csdn.net/xbinworld. 技术交流QQ群:433250724,欢迎对算法.技术感兴趣的同学加入.我的博客写一些自己用得到东西,并分享给 ...
- K-Means 聚类算法
K-Means 概念定义: K-Means 是一种基于距离的排他的聚类划分方法. 上面的 K-Means 描述中包含了几个概念: 聚类(Clustering):K-Means 是一种聚类分析(Clus ...
随机推荐
- Linux学习笔记-第1天(补发)- 新的开始
本来不打算补发第一天的笔记,第一天讲的内容并不多,且大部分内容都是书本上已有的,就没有写多少笔记. 其实在学习的过程中我挺好奇其它同学各种千奇百怪的问题.想法是怎么来的,我怎么想不出来这些.或许这就是 ...
- DP问题(2) : hdu 1421
题目转自hdu 1421,题目传送门 题目大意: 给你n个物品,你要搬走2*k个(也就是搬k次) 每次搬需要花费v,v=(ai-aj)2 (i表示左手拿的物品重量,j表示右手拿的物品的重量) 要求所有 ...
- Mac: phpstorm中使用xdebug调试php
Mac: phpstorm中使用xdebug调试php###phpstorm和webserver都在同一台机器上这种情况1.安装xdebug使用pecl安装即可2.php.ini配置[xdebug]z ...
- 如何备份开拓者TBQuant的策略文件
备份 "C:\TBQuant_V1.1.0.9_X64\users\你的用户名\Strategy\data\strategy.bin" 这个文件即可.
- 实验一 Linux基础与Java开发环境
实验一 (一)实验内容 基于命令行和IDE(Intellj IDEA 简易教程http://www.cnblogs.com/rocedu/p/4421202.html)进行简单的Java程序编辑.编译 ...
- java基础-温故而知新
1.类和对象(实例)的关系 类就是对象的抽象(模板),对象就是类的实例 2.java设置模式--代理模式 定义:代理就是中介,例如租房子经常有中介,还有出票软件 飞猪,携程. 3.代理大纲分为两种:静 ...
- 基于canvas自动化运维工具
首先我们的工具绝对顶尖,绝对绚丽.如果有需要代码,可以加我微信索取.18500591275 前几天有个客户找到我,问我这个能不能做,我看自己也干了10年前端了,实在做不了,后来人家说给你10000你能 ...
- Java8 新特性 Data Time API
Java8新的日期类型 在Java8以前,Date日期API对我们非常的不友好,它无法表示日期,只能以毫秒的精试来表示时间,并且可以修改,他的线程还不是安全的.所以Java8中引入了全新的日期和时间A ...
- layer弹出框,zIndex不断增加的问题
针对layer弹出框每次进行弹出操作时z-index不断加1的问题,手动设置过zIndex值不管用,每次关闭时清空layer对象也不管用. 解决办法: 修改layer.js,,将红框代码改为绿框代码, ...
- XMLHttpRequest原生方法
时间久了,在工作中会有很多方法和见解. 随着时间的推移,慢慢的写的代码越来越多,封装分方法也越来越多,为的是方便后续工作,加快开发效率! 与此同时,我们会相应的去找一些插件,来代替我们在开发过程中执行 ...
