Statistical Methods for Machine Learning

机器学习中的统计学方法。

从机器学习的核心视角来看，优化(optimization)和统计(statistics)是其最最重要的两项支撑技术。统计的方法可以用来机器学习，比如：聚类、贝叶斯等等，当然机器学习还有很多其他的方法，如神经网络（更小范围）、SVM。

机器学习约等于统计+优化，它可以看作是一个方法，用来进行模式识别或数据挖掘。但对于统计和运筹学这俩门基础学科来说，又是应用（见下面四类问题），它大量地用到了统计的模型如马尔可夫随机场（Markov Random Field--MRF），最后转化成一个能量最小化的优化问题。机器学习里面最重要的四类问题（应用）：预测（Prediction）--可以用回归（Regression），聚类（Clustering）--如K-means方法，分类（Classification）--如支持向量机法（SVM），降维（Dimensional reduction）--如主成份分析法（Principal component analysis (PCA)）。【知乎，@留德华叫兽】

原始观察仅仅是数据, 但它们不是信息或知识。数据引发问题, 例如:

• 什么是最常见的或预期的观察？
• 观察的限制是什么？
• 数据是什么样子的？

• 哪些变量最相关？
• 两个实验的区别是什么？
• 这些差异是真实的还是数据中噪音的结果？

众数(mode)、平均数(Mean)和中位数(Median)

众数、平均数和中位数在某些情况下测量的都是数据的中心。

下面两个公式分别计算的是sample和population的平均数：

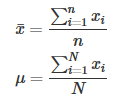
要想找出数据的中位数，我们首先要给数据排序。假设我们有n个已经排好序的数，它们是x1,x2,x3,…,xn。下面是找出它们中位数的公式：

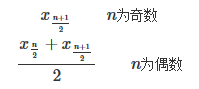
Q1、Q3、IQR、方差和标准差

参见Boxplot。请看下图：

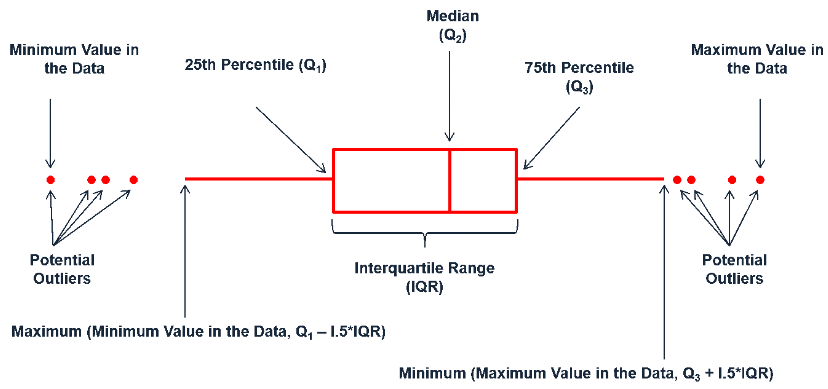
上图中已经很明白地说明Q1、Q3和IQR各自的含义了。从上图我们也看到了小于Q1−1.5∗IQR或大于Q3+1.5∗IQR是可能存在的异常值。在一些情况下，统计学家用这样的方法去掉异常值。

下面，介绍一个找Q1、Q3的方法。

找到Q2，也就是数据集的Median，因此把数据集分成两部分

• 找上半部分的Median，即Q3
• 找下半部分的Median，即Q1

方差和标准差度量的是数据的分散程度。计算方差和标准差的公式如下：

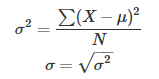
但是绝对值不是更简单明了吗，它也可以度量数据的分散程度啊？为什么我们要费这么大功夫去平方然后在开根号求标准差？这是因为在统计分析中，标准差有一些很Cool的性质。

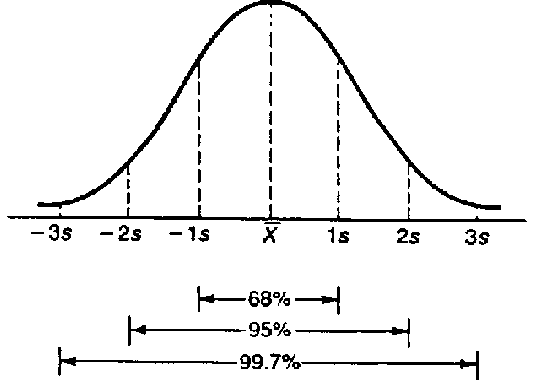
从上图我们可以看出，在正态分布中，有大约68%的数据落在距离平均值1个标准差的范围内，有大约95%的数据落在距离平均值2个标准差的范围内，等等。实际上，我们可以求出任意百分比的数据落在什么样的标准差范围内。因此，求出标准差至关重要。

如果我们的数据集是整个population，那么求标准差的公式和上面的一样。但是如果我们的数据集仅仅是从population中抽取的sample，我们的公式如下：

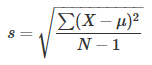
把它叫做Sample standard deviation. 直观上来讲，population中数据大多数都分布在中心，因此我们的Sample中的数据基本上都来自于中心，这样所计算出的标准差要比真实的标准差要小，因为它的数据分散程度要小。因此我们要用N-1来求解（叫做Bessel’s Correction），这样会使我们求出的标准差更加接近真实的标准差。Sample standard deviation也就是population标准差σ的估算。

Z-Score和正态分布

z-score表示一个元素与mean之间相差几个标准差。它的计算公式如下：

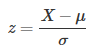
• X：元素的值
• μ：平均值

• σ：标准差

当我们standardization正态分布时（即z-score过程），我们将得到一个标准的正态分布，即平均值为0，标准差为1的正态分布。

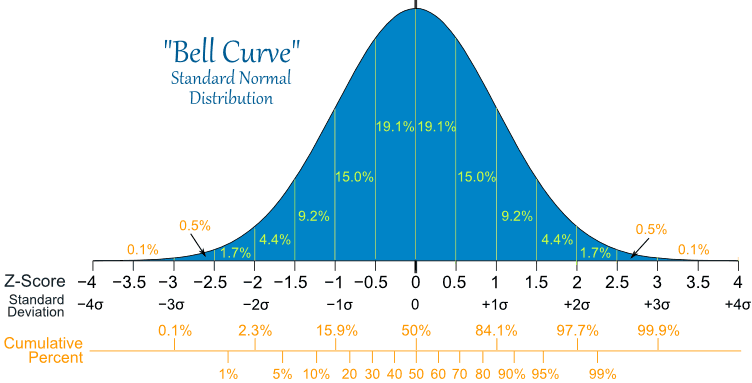
在上图中的正态分布中，X轴上随机选择一个小于x的概率等于负无穷到x与曲线形成的面积。

可以用微积分的知识求出任意两点与曲线之间形成的面积。我们也可以用Z-Table来求出小于某个x值的面积。但是，在用Z-Table之前，我们必须要把正态分布standardization，也就是求出对应x值的z-score。

中心极限定理（Central limit theorem）

假设一个sample包含很多的observations，每个observation是随机生成的并且它们之间是相互独立的，计算这个sample的平均值。重复计算这样sample的平均值，中心极限定理告诉我们这些平均值服从正态分布。

在概率理论中，中心极限定理的定义为：在特定的条件下，不管潜在的population分布是什么样的，大量重复地计算独立随机变量的算术平均值，这些平均值将服从正态分布。

抽样分布（Sampling Distribution）

维基百科上给出抽样分布的定义为：In statistics, a sampling distribution or finite-sample distribution is the probability distribution of a given statistic based on a random sample.

举个例子，假设我们有一个mean为μ，方差为σ²的正态分布。我们重复地从这个population中取出samples，然后分别计算每个sample的平均值，这个统计值叫做sample mean.

每个sample都有一个平均值，这些平均值的分布叫做sampling distribution of the sample mean.

由于population的分布是正态分布，这个分布也是正态分布，它服从N(μ, σ²/n)，这里n为sample size. 根据中心极限定理，即使population分布不是正态的，sampling distribution也通常接近于正态分布。

例子

以下是应用机器学习项目中使用统计方法的10个例子。

• 问题框架: 需要使用探索性数据分析和数据挖掘。
• 数据理解: 需要使用摘要统计信息和数据可视化。
• 数据清洗。需要使用异常检测、归一化等。
• 数据选择。需要使用数据取样和特征选择方法。
• 数据准备。需要使用数据转换、缩放、编码等等。

• 模型计算。需要实验设计和重新取样方法。
• 模型配置。需要使用统计假设测试和估计统计。
• 模型选择。需要使用统计假设测试和估计统计。
• 模型表示。需要使用估计统计信息, 如置信区间。
• 模型预测。需要使用估计统计信息, 如预测间隔。