从图(Graph)到图卷积(Graph Convolution)：漫谈图神经网络模型 (三)

本文属于图神经网络的系列文章，文章目录如下：

恭喜你看到了本系列的第三篇！前面两篇博客分别介绍了基于循环的图神经网络和基于卷积的图神经网络，那么在本篇中，我们则主要关注在得到了各个结点的表示后，如何生成整个图的表示。其实之前我们也举了一些例子，比如最朴素的方法，例如图上所有结点的表示取个均值，即可得到图的表示。那有没有更好的方法呢，它们各自的优点和缺点又是什么呢，本篇主要对上面这两个问题做一点探讨。篇幅不多，理论也不艰深，请读者放心地看。

图读出操作(ReadOut)

图读出操作，顾名思义，就是用来生成图表示的。它的别名有图粗化(翻译捉急，Graph Coarsening)/图池化(Graph Pooling)。对于这种操作而言，它的核心要义在于：操作本身要对结点顺序不敏感。

这是为什么呢？这就不得不提到图本身的一些性质了。我们都知道，在欧氏空间中，如果一张图片旋转了，那么形成的新图片就不再是原来那张图片了；但在非欧式空间的图上，如果一个图旋转一下，例如对它的结点重新编号，这样形成的图与原先的图其实是一个。这就是典型的图重构(Graph Isomorphism)问题。比如下面左右两个图，其实是等价的：

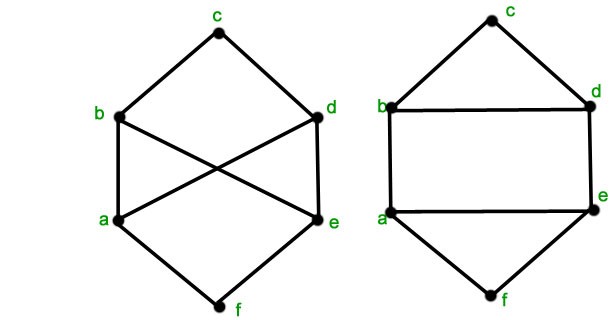
为了使得同构图的表示能够保持一致，图读出的操作就需要对结点顺序不敏感。在数学上，能表达这种操作的函数也被称为对称函数。

那么我们一般如何实现图读出操作呢？笔者接下来主要介绍两种方法：基于统计的方法 与 基于学习的方法。

基于统计的方法(Statistics Category)

基于统计的方法应该是最常见的，比如说我们在求各种抽象表示所使用的 平均(mean)，求和(sum)，取最大(max) 等操作。这些方法简单有效，又不会带来额外的模型参数。但同时我们必须承认，这些方法的信息损失太大。假设一个图里有 1000个结点，每个结点的表示是 100维；整张图本可表达 1000 * 100 的特征，这些简单的统计函数却直接将信息量直接压缩到了100维。尤其是，在这个过程中，每一维上数据的分布特性被完全抹除。

考虑到这一点，文献[1]的作者就提出要用类似直方图的方法来对每维数据分布进行建模。具体而言，请读者先通过下面的对比图来直观感受一下直方图是如何巧妙平衡数据信息的压缩与增强的。假设我们有100个介于[-3,1]的数字，如果我们直接将它们求和，如左图所示，我们完全看不出这100个数据的分布；而如果我们将[-3, 1]等分成4个区域，比如说就是[-3,-2),[-2,-1),[-1,0) 和 [0,1)。我们分开统计各个区域的和，可以发现一点原数据的分布特征，就如下右侧子图所示：

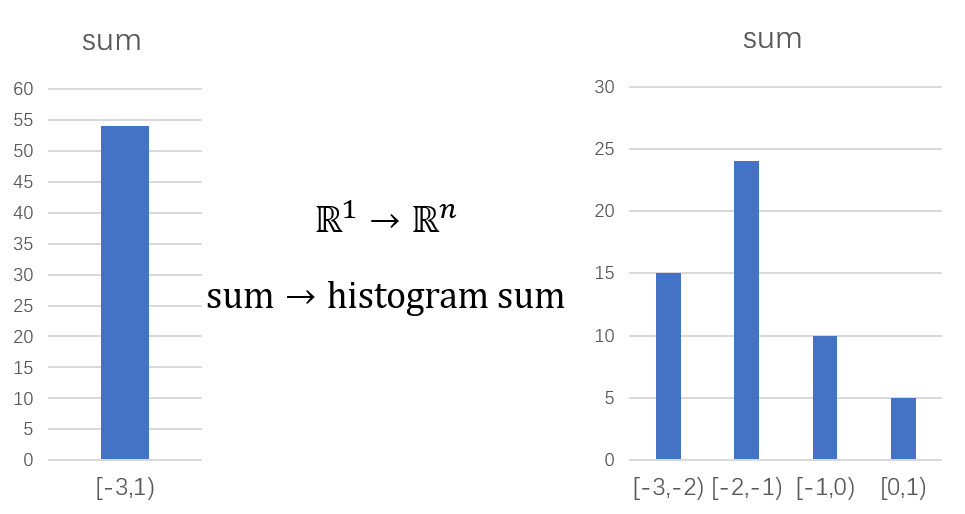
如果要实现上面这个直方图的做法，该如何做呢？其实也很简单，我们举个例子。给定3个数据点，它们的特征向量(2维)分别是[-2, 1], [-1, 2] 和 [-1, 1]。如果直接求和，全局的特征向量是 [-2+-1+-1, 1+2+1] 即 [-4,4]。如果采取上述直方图的方式，则可能会得到一个这样的全局特征向量[-2, -1 + -1, 1 + 1, 2](第1,2维代表从原先的第1维统计的直方图,对应的区域为[-2,1),[1,2),第3,4维的含义类似)。但在实践中，文献[1]没有直接利用这种方法，而是采用高斯函数来实现名为模糊直方图(Fuzzy Histogram)的操作。

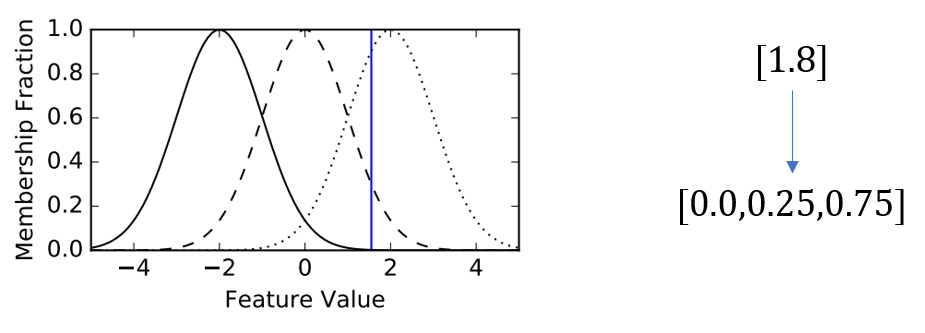
模糊直方图的原理也很简单：预先定义几个特征值区域的边界点为各个高斯分布的均值，并预设好方差。对任一特征值，根据其与各个高斯分布交点的纵坐标作为其落入该区域的数值，然后将所有数值归一化，就得到了该特征值分布在各个区间的比例。举个例子，图上的[1.8]与三个高斯分布的交点分别在0,0.3,0.9处，归一化一下，即可知该特征值最终应该用一个3维向量[0.0, 0.25, 0.75]来表示。

基于学习的方法(Learning Category)

基于统计的方法的一个坏处大概是它没办法参数化，间接地难以表示结点到图向量的这个“复杂”过程。基于学习的方法就是希望用神经网络来拟合这个过程。

采样加全连接(Sample And FC)

最简单又最直接的做法，大概就是取固定数量的结点，通过一个全连接层(Fully Connected Layer)得到图的表示。这里不论是随机采样也好，还是根据某些规则采样，都需要得到确定数量的结点，如果不够就做填充。公式也很简单直接（\(\textbf{H}^