POJ 3565 Ants 【最小权值匹配应用】

传送门：http://poj.org/problem?id=3565

Ants

Time Limit: 5000MS		Memory Limit: 65536K
Total Submissions: 7650		Accepted: 2424		Special Judge

Description

Young naturalist Bill studies ants in school. His ants feed on plant-louses that live on apple trees. Each ant colony needs its own apple tree to feed itself.

Bill has a map with coordinates of n ant colonies and n apple trees. He knows that ants travel from their colony to their feeding places and back using chemically tagged routes. The routes cannot intersect each other or ants will get confused and get to the wrong colony or tree, thus spurring a war between colonies.

Bill would like to connect each ant colony to a single apple tree so that all n routes are non-intersecting straight lines. In this problem such connection is always possible. Your task is to write a program that finds such connection.

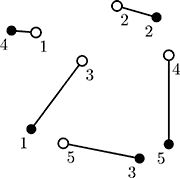
On this picture ant colonies are denoted by empty circles and apple trees are denoted by filled circles. One possible connection is denoted by lines.

Input

The first line of the input file contains a single integer number n (1 ≤ n ≤ 100) — the number of ant colonies and apple trees. It is followed by n lines describing n ant colonies, followed by n lines describing n apple trees. Each ant colony and apple tree is described by a pair of integer coordinates x and y (−10 000 ≤ x, y ≤ 10 000) on a Cartesian plane. All ant colonies and apple trees occupy distinct points on a plane. No three points are on the same line.

Output

Write to the output file n lines with one integer number on each line. The number written on i-th line denotes the number (from 1 to n) of the apple tree that is connected to the i-th ant colony.

Sample Input

5
-42 58
44 86
7 28
99 34
-13 -59
-47 -44
86 74
68 -75
-68 60
99 -60

Sample Output

4
2
1
5
3

Source

Northeastern Europe 2007

题意概括：

给出 N 个蚂蚁的坐标 ( x1, y1 ), N 个苹果树的坐标 ( x2, y2 )，将蚂蚁和苹果树两两配对，但是路径不能相交。

按顺序输出 第 i 个蚂蚁匹配到第几棵苹果树。

解题思路：

最小权值匹配的应用：做小权值匹配就保证了两两不相交，为什么呢？

这是因为如果最小权匹配有两条线段相交，那么一定可以转化为两条不相交且总长度更短的两条线段（三角形斜边一定小于另外两边之和嘛），这与最小权矛盾，所以可以证明最小权匹配中没有相交的线段。

AC code：

 #include <cstdio>
 #include <iostream>
 #include <algorithm>
 #include <cstring>
 #include <cmath>
 using namespace std;
 const int MAXN = ;
 const double INF = 0x3f3f3f3f;
 struct date
 {
     double x, y;
 }node1[MAXN], node2[MAXN];

 double a[MAXN][MAXN];  //二分图；
 double ex[MAXN], ey[MAXN];
 int linker[MAXN];
 bool visx[MAXN], visy[MAXN];
 double slack[MAXN];
 int N;

 bool Find(int x)
 {
     visx[x] = true;
     for(int y = ; y <= N; y++){
         if(visy[y]) continue;
         double t = ex[x] + ey[y] - a[x][y];
         if(t < 1e-){
             visy[y] = true;
             if(linker[y] == - || Find(linker[y])){
                 linker[y] = x;
                 return true;
             }
         }
         else
         {
             slack[y] = min(slack[y], t);
         }
     }
     return false;
 }

 void KM()
 {
     ///初始化
     memset(linker, -, sizeof(linker));
     memset(ey, , sizeof(ey));

     for(int i = ; i <= N; i++){
         ex[i] = a[i][];
         for(int j = ; j <= N; j++){
             ex[i] = max(ex[i], a[i][j]);
         }
     }

     for(int x = ; x <= N; x++){

         fill(slack, slack++N, INF);

         while(){
             memset(visx, , sizeof(visx));
             memset(visy, , sizeof(visy));
             if(Find(x)) break;
             double min_slack = INF;
             for(int i = ; i <= N; i++){
                 if(!visy[i])
                     min_slack = min(min_slack, slack[i]);
             }
             for(int i = ; i <= N; i++){
                 if(visx[i]) ex[i]-=min_slack;
             }
             for(int j = ; j <= N; j++){
                 if(visy[j]) ey[j]+=min_slack;
             }
         }
     }
 }

 //double dis(date n1, date n2)
 //{
 //    double res = 0;
 //    res = sqrt((n1.x - n2.x)*(n1.x - n2.x) + (n1.y - n2.y)*(n1.y - n2.y));
 //    return -res;
 //}

 int main()
 {
     while(~scanf("%d", &N)){
 //        init();
         for(int i = ; i <= N; i++){
             scanf("%lf%lf", &node1[i].x, &node1[i].y);
         }
         for(int i = ; i <= N; i++){
             scanf("%lf%lf", &node2[i].x, &node2[i].y);
         }
         for(int i = ; i <= N; i++)
         for(int j = ; j <= N; j++){
             a[j][i] = -sqrt((node1[i].x - node2[j].x)*(node1[i].x - node2[j].x) + (node1[i].y - node2[j].y)*(node1[i].y - node2[j].y));
         }
         KM();
         for(int i = ; i <= N; i++){
             printf("%d\n", linker[i]);
         }
     }
     return ;
 }