loj #535. 「LibreOJ Round #6」花火 树状数组求逆序对+主席树二维数点+整体二分

$ \color{#0066ff}{ 题目描述 }$

「Hanabi, hanabi……」

一听说祭典上没有烟火，Karen 一脸沮丧。

「有的哦…… 虽然比不上大型烟花就是了。」

还好 Shinobu 早有准备，Alice、Ayaya、Karen、Shinobu、Yoko 五人又能继续愉快地玩耍啦！

「噢……！不是有放上天的烟花嘛！」Karen 兴奋地喊道。

「啊等等……」Yoko 惊呼。Karen 手持点燃引信的烟花，「嗯？？」

Yoko 最希望见到的是排列优美的烟火，当然不会放过这个机会…… 不过时间似乎已经不多了。

nn 个烟火排成一排，从左到右高度分别为 \(h_1,h_2,\cdots\)，这些高度两两不同。

每次 Yoko 可以选择两个相邻的烟火交换，这样的交换可以进行任意多次。

每次 Yoko 还可以选择两个不相邻的烟火交换，但这样的交换至多进行一次。

你的任务是帮助 Yoko 用最少次数的交换，使这些烟火从左到右的高度递增。

\(\color{#0066ff}{输入格式}\)

第一行包含一个正整数 \(n\)。

第二行包含 \(n\) 个正整数 \(h_1,h_2,\cdots\)，相邻整数之间用一个空格隔开。

\(\color{#0066ff}{输出格式}\)

输出一个整数，表示最少的交换次数。

\(\color{#0066ff}{输入样例}\)

5
3 5 4 1 2

\(\color{#0066ff}{输出样例}\)

5

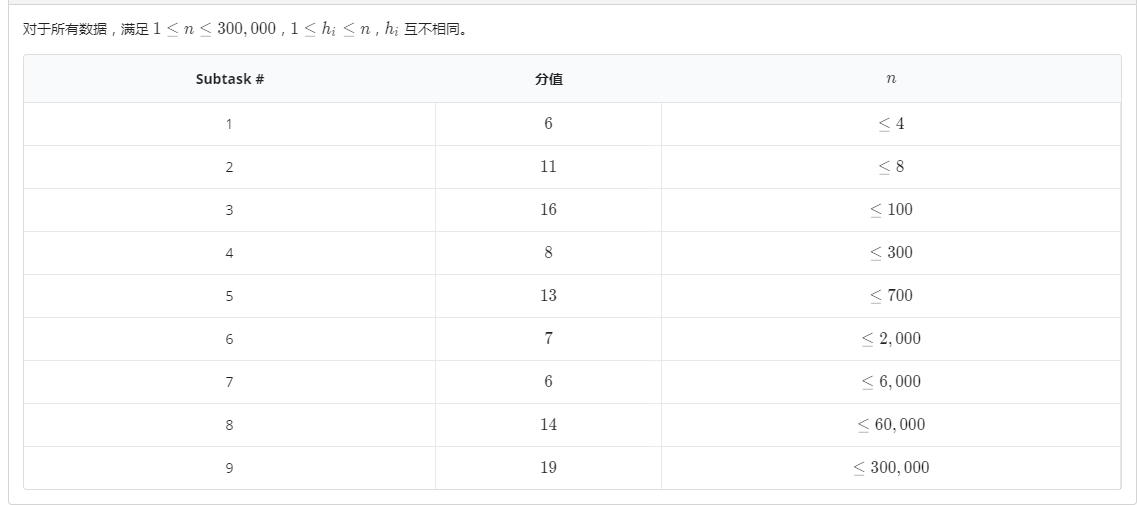
\(\color{#0066ff}{数据范围与提示}\)

一开始，\(5\) 个烟火的高度依次为 \(3,5,4,1,2\)。

第 \(1\) 次，交换第 \(4\) 根烟火和第 \(5\) 根烟火，交换后烟火的高度依次为 \(3,5,4,2,1\)。

第 \(2\) 次，交换第 \(3\) 根烟火和第 \(4\) 根烟火，交换后烟火的高度依次为 \(3,5,2,4,1\)。

第 \(3\) 次，交换第 \(1\) 根烟火和第 \(2\) 根烟火，交换后烟火的高度依次为 \(5,3,2,4,1\)。

第 \(4\) 次，交换第 \(2\) 根烟火和第 \(3\) 根烟火，交换后烟火的高度依次为 \(5,2,3,4,1\)。

第 \(5\) 次，交换第 \(1\) 根烟火和第 \(5\) 根烟火，交换后烟火的高度依次为 \(1,2,3,4,5\)。

可以证明这是交换次数最少的方案。

\(\color{#0066ff}{题解}\)

考虑没有交换任意两个数一次的操作，那么答案就是逆序对数

现在我们有一个交换任意两个数的操作

我们肯定是要让这次操作的贡献最大的

也就是说，减少的逆序对数最多

那么我们选的两个数，左面那个肯定是越靠左且越大为优，右面那个越靠右越小越优

也就是说，我们可能被交换的数就是所有前缀max取得的点和所有后缀min取得的点

然后我们处理出了这两个可能修改的位置数组，都是单调的

我们现在要在两个数组内分别选一个数，交换这两个数所对应的位置，使得对答案的贡献最大

对于一对\([l,r]\)，交换它俩的贡献是\([l,r]之间权值在[a[r],a[l]]之间的值的个数\)

这就是二维数点了， 主席树可以维护

现在考虑怎么快速求出每个点的贡献

也就是说，对于每个可能的右端点，选一个最优的左端点

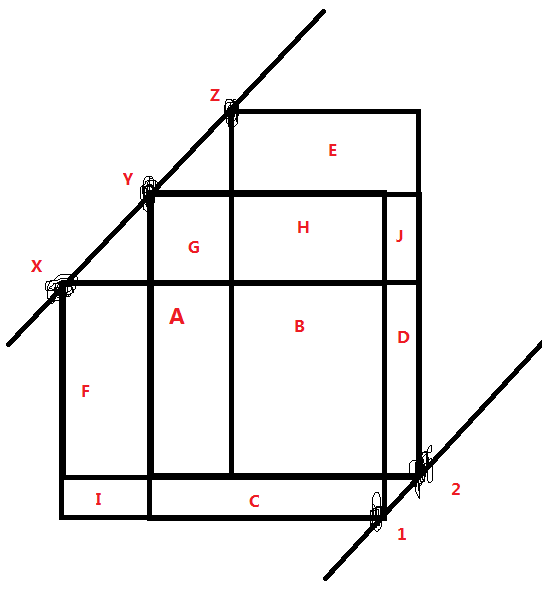
我们假设1选择y最优

那么可以得出\(G+H>F+I\)

然后对于2，因为\(G+H+J>F\)显然，所以y肯定比x有，也就是说最优点单调！！

于是我们就可以整体二分\(O(nlog^2n)\)的求出右面每个点的贡献，然后取max，交换最优的l和r

最后树状数组求一下序列逆序对即可

#include<bits/stdc++.h>
#define LL long long
LL in() {
	char ch; LL x = 0, f = 1;
	while(!isdigit(ch = getchar()))(ch == '-') && (f = -f);
	for(x = ch ^ 48; isdigit(ch = getchar()); x = (x << 1) + (x << 3) + (ch ^ 48));
	return x * f;
}
const int maxn = 3e5 + 10;
struct Tree {
protected:
	int st[maxn];
	int low(int x) { return x & (-x); }
	int siz;
public:
	void resize(int n) { siz = n; }
	void add(int pos) { while(pos <= siz) st[pos]++, pos += low(pos); }
	int query(int pos) { int re = 0; while(pos) re += st[pos], pos -= low(pos); return re; }
}s;
struct node {
	node *ch[2];
	int num;
	node(int num = 0): num(num) { ch[0] = ch[1] = NULL; }
};
int n, a[maxn];
node *root[maxn];
int st1[maxn], st2[maxn], top1, top2, to[maxn], ans[maxn];
LL tot;
void init() {
	root[0] = new node();
	root[0]->ch[0] = root[0]->ch[1] = root[0];
}
void add(node *&o, node *lst, int l, int r, int p) {
	o = new node(), *o = *lst, o->num++;
	if(l == r) return;
	int mid = (l + r) >> 1;
	if(p <= mid) add(o->ch[0], lst->ch[0], l, mid, p);
	else add(o->ch[1], lst->ch[1], mid + 1, r, p);
}
int getnum(node *x, node *y, int l, int r, int ql, int qr) {
	if(x->num == y->num) return 0;
	if(ql <= l && r <= qr) return y->num - x->num;
	int mid = (l + r) >> 1;
	int cnt = 0;
	if(ql <= mid) cnt += getnum(x->ch[0], y->ch[0], l, mid, ql, qr);
	if(qr > mid) cnt += getnum(x->ch[1], y->ch[1], mid + 1, r, ql, qr);
	return cnt;
}
int getans(int l, int r) {
	if(l >= r) return 0;
	if(a[l] < a[r]) return 0;
	return getnum(root[l - 1], root[r], 1, n, a[r] + 1, a[l] - 1);
}
void cdq(int l, int r, int a, int b) {
	if(a > b) return;
	if(l > r) return;
	if(l == r) {
		for(int i = a; i <= b; i++) {
			int now = getans(st1[l], st2[i]);
			if(now > ans[i]) ans[i] = now, to[i] = l;
		}
		return;
	}
	int mid = (a + b) >> 1;
	//printf("now is work[%d, %d, %d, %d]\n", l, r, a, b);
	ans[mid] = 0;
	for(int i = l; i <= r; i++) {
		int now = getans(st1[i], st2[mid]);
		if(now >= ans[mid]) ans[mid] = now, to[mid] = i;
	}
	cdq(l, to[mid], a, mid - 1);
	cdq(to[mid], r, mid + 1, b);
}
void predoit() {
	s.resize(n);
	init();
	for(int i = 1; i <= n; i++) add(root[i], root[i - 1], 1, n, a[i] = in());
	//st1 can be left
	//st2 can be right
	for(int i = 1; i <= n; i++) {
		while(top2 && a[i] < a[st2[top2]]) top2--;
		if(a[i] > a[st1[top1]]) st1[++top1] = i;
		st2[++top2] = i;
	}
	int max = 0, l = 0, r = 0;
	cdq(1, top1, 1, top2);
	for(int i = 1; i <= top2; i++)
		if(max < ans[i]) max = ans[i], l = st1[to[i]], r = st2[i];
	std::swap(a[l], a[r]);
	if(l ^ r) tot++;
}
void getans() {
	for(int i = n; i >= 1; i--) {
		tot += s.query(a[i]);
		s.add(a[i]);
	}
	printf("%lld\n", tot);
}
int main() {
	n = in();
	predoit();
	getans();
	return 0;
}