tarjan求强连通分量+缩点+割点以及一些证明

“tarjan陪伴强联通分量

生成树完成后思路才闪光

欧拉跑过的七桥古塘

让你 心驰神往”----《膜你抄》

 

自从听完这首歌，我就对tarjan开始心驰神往了，不过由于之前水平不足，一直没有时间学习。这两天好不容易学会了，写篇博客，也算记录一下。

 

一、tarjan求强连通分量

1、什么是强连通分量？

引用来自度娘的一句话：

“有向图强连通分量：在有向图G中，如果两个顶点vi,vj间（vi>vj）有一条从vi到vj的有向路径，同时还有一条从vj到vi的有向路径，则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通，称G是一个强连通图。有向图的极大强连通子图，称为强连通分量(strongly connected components)。”

一脸懵逼......不过倒也不难理解。

反正就是在图中找到一个最大的图，使这个图中每个两点都能够互相到达。这个最大的图称为强连通分量，同时一个点也属于强连通分量。

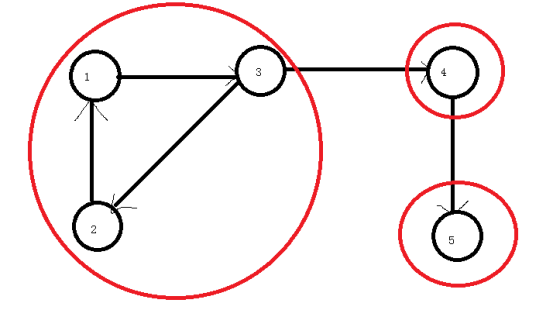
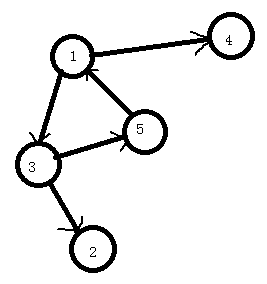
如图中强连通分量有三个：1-2-3,4,5

 

2、强连通分量怎么找？

噫......当然，通过肉眼可以很直观地看出1-2-3是一组强连通分量，但很遗憾，机器并没有眼睛，所以该怎么判断强连通分量呢？

如果仍是上面那张图，我们对它进行dfs遍历。

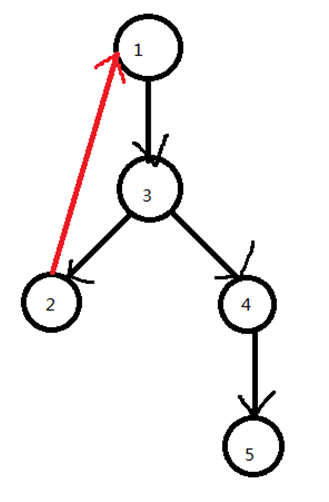
可以注意到红边非常特别，因为如果按照遍历时间来分类的话，其他边都指向在自己之后被遍历到的点，而红边指向的则是比自己先被遍历到的点。

 

如果存在这么一条边，那么我们可以yy一下，emmmm.......

从一个点出发，一直向下遍历，然后忽得找到一个点，那个点竟然有条指回这一个点的边！

那么想必这个点能够从自身出发再回到自身

想必这个点和其他向下遍历的该路径上的所有点构成了一个环，

想必这个环上的所有点都是强联通的。

但只是强联通啊，我们需要求的可是强连通分量啊......

 

那怎么办呢？

我们还是yy出那棵dfs树

不妨想一下，什么时候一个点和他的所有子孙节点中的一部分构成强连通分量？

他的子孙再也没有指向他的祖先的边，却有指向他自己的边

因为只要他的子孙节点有指向祖先的边，显然可以构成一个更大的强联通图。

 

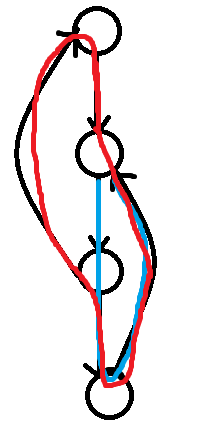
比如说图中红色为强连通分量，而蓝色只是强联通图

 

那么我们只需要知道这个点u下面的所有子节点有没有连着这个点的祖先就行了。

但似乎还有一个问题啊......

 

我们怎么知道这个点u它下面的所有子节点一定是都与他强联通的呢？

这似乎是不对的，这个点u之下的所有点不一定都强联通

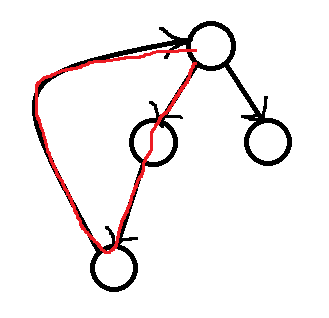
那么怎么在退回到这个点的时候，知道所有和这个点u构成强连通分量的点呢？

开个栈记录就行了

什么？！这么简单？

没错~就是这么简单~

如果在这个点之后被遍历到的点已经能与其下面的一部分点（也可能就只有他一个点）已经构成强连通分量，即它已经是最大的。

那么把它们一起从栈里弹出来就行了。

所以最后处理到点u时如果u的子孙没有指向其祖先的边，那么它之后的点肯定都已经处理好了，一个常见的思想，可以理解一下。

所以就可以保证栈里留下来u后的点都是能与它构成强连通分量的。

 

似乎做法已经明了了，用程序应该怎么实现呢？

 

所以为了实现上面的操作，我们需要一些辅助数组

(1)、dfn[ ]，表示这个点在dfs时是第几个被搜到的。

(2)、low[ ]，表示这个点以及其子孙节点连的所有点中dfn最小的值

(3)、stack[ ]，表示当前所有可能能构成是强连通分量的点。

(4)、vis[ ]，表示一个点是否在stack[ ]数组中。

那么按照之上的思路，我们来考虑这几个数组的用处以及tarjan的过程。

 

假设现在开始遍历点u：

 

(1)、首先初始化dfn[u]=low[u]=第几个被dfs到

dfn可以理解，但为什么low也要这么做呢？

 因为low的定义如上，也就是说如果没有子孙与u的祖先相连的话，dfn[u]一定是它和它的所有子孙中dfn最小的（因为它的所有子孙一定比他后搜到）。

 

(2)、将u存入stack[ ]中，并将vis[u]设为true

stack[ ]有什么用？

如果u在stack中，u之后的所有点在u被回溯到时u和栈中所有在它之后的点都构成强连通分量。

 

(3)、遍历u的每一个能到的点，如果这个点dfn[ ]为0，即仍未访问过，那么就对点v进行dfs，然后low[u]=min{low[u],low[v]}

low[ ]有什么用？

应该能看出来吧，就是记录一个点它最大能连通到哪个祖先节点（当然包括自己）

如果遍历到的这个点已经被遍历到了，那么看它当前有没有在stack[ ]里,如果有那么low[u]=min{low[u],low[v]}

如果已经被弹掉了，说明无论如何这个点也不能与u构成强连通分量，因为它不能到达u

如果还在栈里，说明这个点肯定能到达u，同样u能到达他，他俩强联通。

 

(4)、假设我们已经dfs完了u的所有的子树那么之后无论我们再怎么dfs，u点的low值已经不会再变了。

那么如果dfn[u]=low[u]这说明了什么呢？

再结合一下dfn和low的定义来看看吧

dfn表示u点被dfs到的时间，low表示u和u所有的子树所能到达的点中dfn最小的。

这说明了u点及u点之下的所有子节点没有边是指向u的祖先的了，即我们之前说的u点与它的子孙节点构成了一个最大的强连通图即强连通分量

此时我们得到了一个强连通分量，把所有的u点以后压入栈中的点和u点一并弹出，将它们的vis[ ]置为false，如有需要也可以给它们打上相同标记（同一个数字）

 

tarjan到此结束

至于手模？tan90°！网上有不少大佬已经手摸了不少样例了，想必不需要本蒟蒻再补充了。

 

结合上面四步代码已经可以写出了：

对了，tarjan一遍不能搜完所有的点，因为存在孤立点或者其他

所以我们要对一趟跑下来还没有被访问到的点继续跑tarjan

怎么知道这个点有没有被访问呢？

看看它的dfn是否为0！

这看起来似乎是o(n^2)的复杂度，但其实均摊下来每个点只会被遍历一遍

所以tarjan的复杂度为o(n)。

 

来一道例题吧，这是模板题，应该做到提交框AC

[USACO06JAN]牛的舞会The Cow Prom

 给你n个点，m条边，求图中所有大小大于1的强连通分量的个数

输入样例#1：

5 4
2 4
3 5
1 2
4 1

输出样例#1： 

1

显然是tarjan水题，数出强连通分量的个数，给每个强连通分量的点染色，统计出每个强连通分量中点的个数，如果大于一，则答案加一。

代码：

#include<queue>
#include<cstdio>
#include<vector>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define inf 0x3f3f3f3f

vector<int> g[];
int color[],dfn[],low[],stack[],vis[],cnt[];
int deep,top,n,m,sum,ans;

void tarjan(int u)
{
    dfn[u]=++deep;
    low[u]=deep;
    vis[u]=;
    stack[++top]=u;
    int sz=g[u].size();
    for(int i=;i<sz;i++)
    {
        int v=g[u][i];
        if(!dfn[v])
        {
            tarjan(v);
            low[u]=min(low[u],low[v]);
        }
        else
        {
            if(vis[v])
            {
                low[u]=min(low[u],low[v]);
            }
        }
    }
    if(dfn[u]==low[u])
    {
        color[u]=++sum;
        vis[u]=;
        while(stack[top]!=u)
        {
            color[stack[top]]=sum;
            vis[stack[top--]]=;
        }
        top--;
    }
}

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=;i<=m;i++)
    {
        int from,to;
        scanf("%d%d",&from,&to);
        g[from].push_back(to);
    }
    for(int i=;i<=n;i++)
    {
        if(!dfn[i])
        {
            tarjan(i);
        }
    }
    for(int i=;i<=n;i++)
    {
        cnt[color[i]]++;
    }
    for(int i=;i<=sum;i++)
    {
        if(cnt[i]>)
        {
            ans++;
        }
    }
    printf("%d\n",ans);
}

 

二、tarjan缩点

其实这也是利用了tarjan求强连通分量的方法，对于一些贡献具有传导性，比如友情啊、路径上的权值啊等等。

思想就是因为强连通分量中的每两个点都是强连通的，可以将一个强连通分量当做一个超级点，而点权按题意来定。

 

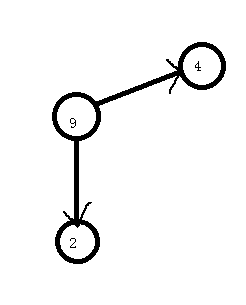
来看一道题吧。

poj2186 Popular Cows

告诉你有n头牛，m个崇拜关系，并且崇拜具有传递性，如果a崇拜b，b崇拜c，则a崇拜c，求最后有几头牛被所有牛崇拜。

 

Sample Input
3 3
1 2
2 1
2 3
Sample Output
1

 

显然一个强联通分量内的所有点都是满足条件的，我们可以对整张图进行缩点，然后就简单了。

剩下的所有点都不是强连通的，现在整张图就是一个DAG（有向无环图）

那么就变成一道水题了，因为这是一个有向无环图，不存在所有点的出度都不为零的情况。

所以必然有1个及以上的点出度为零，如果有两个点出度为零，那么这两个点肯定是不相连的，即这两圈牛不是互相崇拜的，于是此时答案为零，如果有1个点出度为0，那么这个点就是被全体牛崇拜的，

这个点可能是一个强联通分量缩成的超级点，所以应该输出整个强联通分量中点的个数。

代码：

#include<cmath>
#include<cstdio>
#include<vector>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;

int dfn[],low[],vis[],stack[],color[],du[],cnt[];
int n,m,top,sum,deep,tmp,ans;
vector<int> g[];

void tarjan(int u)
{
    dfn[u]=low[u]=++deep;
    vis[u]=;
    stack[++top]=u;
    int sz=g[u].size();
    for(int i=; i<sz; i++)
    {
        int v=g[u][i];
        if(!dfn[v])
        {
            tarjan(v);
            low[u]=min(low[u],low[v]);
        }
        else
        {
            if(vis[v])
            {
                low[u]=min(low[u],low[v]);
            }
        }
    }
    if(dfn[u]==low[u])
    {
        color[u]=++sum;
        vis[u]=;
        while(stack[top]!=u)
        {
            color[stack[top]]=sum;
            vis[stack[top--]]=;
        }
        top--;
    }
}

int main()
{
    while(scanf("%d%d",&n,&m)!=EOF)
    {
        memset(vis,,sizeof(du));
        memset(vis,,sizeof(low));
        memset(dfn,,sizeof(dfn));
        memset(vis,,sizeof(vis));
        memset(vis,,sizeof(cnt));
        memset(vis,,sizeof(color));
        memset(vis,,sizeof(stack));
        for(int i=; i<=n; i++)
        {
            g[i].clear();
        }
        for(int i=; i<=m; i++)
        {
            int from,to;
            scanf("%d%d",&from,&to);
            g[from].push_back(to);
        }
        for(int i=; i<=n; i++)
        {
            if(!dfn[i])
            {
                tarjan(i);
            }
        }
        for(int i=; i<=n; i++)
        {
            int sz=g[i].size();
            for(int j=; j<sz; j++)
            {
                int v=g[i][j];
                if(color[v]!=color[i])
                {
                    du[color[i]]++;
                }
            }
            cnt[color[i]]++;
        }
        for(int i=; i<=sum; i++)
        {
            if(du[i]==)
            {
                tmp++;
                ans=cnt[i];
            }
        }
        if(tmp==)
        {
            printf("0\n");

        }
        else
        {
            if(tmp>)
            {
                printf("0\n");
            }
            else
            {
                printf("%d\n",ans);
            }
        }
    }
}

三、tarjan求割点、桥

1、什么是割点、桥

再来引用一遍度娘：

在一个无向图中，如果有一个顶点集合，删除这个顶点集合以及这个集合中所有顶点相关联的边以后，图的连通分量增多，就称这个点集为割点集合。

又是一脸懵逼。。。。

总而言之，就是这个点维持着双联通的继续，去掉这个点，这个连通分量就无法在维持下去，分成好几个连通分量。

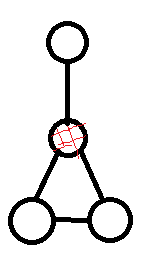
比如说上图红色的即为一个割点。

桥：

如果一个无向连通图的边连通度大于1，则称该图是边双连通的 (edge biconnected)，简 称双连通或重连通。一个图有桥，当且仅当这个图的边连通度为 1，则割边集合的唯一元素 被称为桥(bridge)，又叫关节边(articulationedge)。一个图可能有多个桥。（该资料同样来自百度）

对于连通图有两种双联通，边双和点双，桥之于边双如同割点之于点双

如图则是一个桥。

2、割点和桥怎么求？

与之前强连通分量中的tarjan差不多。但要加一个特判，根节点如果有两个及以上的儿子，那么他也是割点。

 

模板题：洛谷3388

求割点的个数和数量

代码：

#include<cstdio>
#include<vector>
#include<cstring>
#include<iostream>
#include<algorithm>
#define hi printf("hi!");
using namespace std;

vector<int> g[];
int dfn[],low[],iscut[],son[];
int deep,root,n,m,ans;

int tarjan(int u,int fa)
{
    int child=,lowu;
    lowu=dfn[u]=++deep;
    int sz=g[u].size();
    for(int i=;i<sz;i++)
    {
        int v=g[u][i];
        if(!dfn[v])
        {
            child++;
            int lowv=tarjan(v,u);
            lowu=min(lowu,lowv);
            if(lowv>dfn[u])
            {
                iscut[u]=;
            }
        }
        else
        {
            if(v!=fa&&dfn[v]<dfn[u])
            {
                lowu=min(lowu,dfn[v]);
            }
        }
    }
    if(fa<&&child==)
    {
        iscut[u]=false;
    }
    low[u]=lowu;
    return lowu;
} 

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=;i<=m;i++)
    {
        int from,to;
        scanf("%d%d",&from,&to);
        g[from].push_back(to);
        g[to].push_back(from);
    }
    for(int i=;i<=n;i++)
    {
        if(!dfn[i])
        {
            root=i;
            tarjan(i,-);
        }
    }
    for(int i=;i<=n;i++)
    {
        if(iscut[i])
        {
            ans++;
        }
    }
    printf("%d\n",ans);
    for(int i=;i<=n;i++)
    {
        if(iscut[i])
        {
            printf("%d ",i);
        }
    }
}

桥的求法也差不多

 

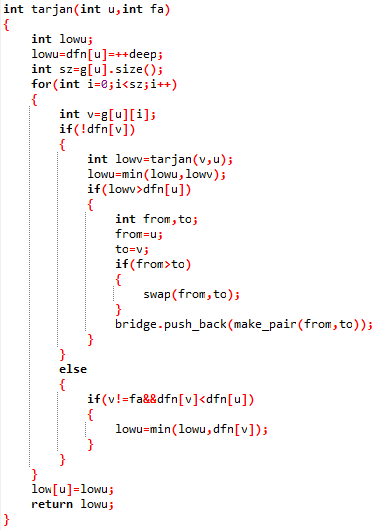
并没有找到模板题目，所以只好把没检验过的代码放着了......如有错误还请留言指正

#include<cstdio>
#include<vector>
#include<cstring>
#include<iostream>
#include<algorithm>
#define hi printf("hi!");
using namespace std;

vector<pair<int,int> >bridge;
vector<int> g[];
int dfn[],low[];
int deep,root,n,m,ans;

int tarjan(int u,int fa)
{
    int lowu;
    lowu=dfn[u]=++deep;
    int sz=g[u].size();
    for(int i=;i<sz;i++)
    {
        int v=g[u][i];
        if(!dfn[v])
        {
            int lowv=tarjan(v,u);
            lowu=min(lowu,lowv);
            if(lowv>dfn[u])
            {
                int from,to;
                from=u;
                to=v;
                if(from>to)
                {
                    swap(from,to);
                }
                bridge.push_back(make_pair(from,to));
            }
        }
        else
        {
            if(v!=fa&&dfn[v]<dfn[u])
            {
                lowu=min(lowu,dfn[v]);
            }
        }
    }
    low[u]=lowu;
    return lowu;
} 

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=;i<=m;i++)
    {
        int from,to;
        scanf("%d%d",&from,&to);
        g[from].push_back(to);
        g[to].push_back(from);
    }
    for(int i=;i<=n;i++)
    {
        if(!dfn[i])
        {
            root=i;
            tarjan(i,-);
        }
    }
    for(int i=;i<bridge.size();i++)
    {
        printf("%d %d\n",bridge[i].first,bridge[i].second);
    }
}

 

 

 

 

おわり