Catalan数——卡特兰数

一、Catalan数的定义

　　令h(0)=1，h(1)=1，Catalan数满足递归式：h(n) = h(0)*h(n-1) + h(1)*h(n-2) + ... + h(n-1)*h(0)  (n>=2)

　　该递推关系的解为：h(n) = C(2n,n)/(n+1)，n=0,1,2,3,... （其中C(2n,n)表示2n个物品中取n个的组合数）

二、问题描述
　　12个高矮不同的人，排成两排，每排必须是从矮到高排列，而且第二排比对应的第一排的人高，问排列方式有多少种？

　　问题分析:
　　我们先把这12个人从低到高排列,然后,选择6个人排在第一排,那么剩下的6个肯定是在第二排.
　　用0表示对应的人在第一排,用1表示对应的人在第二排,那么含有6个0,6个1的序列,就对应一种方案.
　　比如000000111111就对应着
　　第一排：0 1 2 3 4 5
　　第二排：6 7 8 9 10 11
　　010101010101就对应着
　　第一排：0 2 4 6 8 10
　　第二排：1 3 5 7 9 11
　　问题转换为，这样的满足条件的01序列有多少个。

　　观察规律我们发现1的出现前边必须有一个相应的0对应，所以从左到右的所有序列中0的个数要一直大于1的个数。那这种数列有多少种排列方式呢？

　　那么我们从左往右扫描，第一次出现1的个数等于0的个数是第k位，那么在此之前，0的个数是大于1的个数的。在此之后，0的个数也是大于1的个数的。所以第k位0和1的个数第一次相等的排列有他们这两部分的个数相称的结果。那么所有的k有多少种，则把它们相加起来，就是最后的排列数。这是一个递归的问题。

　　即   h(n)=h(0)×h(n-1)+h(1)*h(n-2)+...+h(n-1)*h(0)

　　如果把0看成入栈操作，1看成出栈操作，就是说给定6个元素，合法的入栈出栈序列有多少个。

　　在<<计算机程序设计艺术>>，第三版，Donald E.Knuth著，苏运霖译，第一卷，508页，给出了证明:
　　问题大意是用S表示入栈，X表示出栈，那么合法的序列有多少个(S的个数为n)
　　显然有c(2n, n)个含S，X各n个的序列，剩下的是计算不允许的序列数(它包含正确个数的S和X，但是违背其它条件)。
　　在任何不允许的序列中，定出使得X的个数超过S的个数的第一个X的位置。然后在导致并包括这个X的部分序列中，以S代替所有的X并以X代表所有的S。结果是一个有(n+1)个S和(n-1)个X的序列。反过来，对一垢一种类型的每个序列，我们都能逆转这个过程，而且找出导致它的前一种类型的不允许序列。例如XXSXSSSXXSSS必然来自SSXSXXXXXSSS。这个对应说明，不允许的序列的个数是c(2n, n-1)，因此h(n )= c(2n, n) - c(2n, n-1)。

三、递推公式

　另类递推式：

　　h(n)=h(n-1)*(4*n-2)/(n+1)

　递推关系的解为：

　　h(n)=C(2n,n)/(n+1) (n=0,1,2,...)

　递推关系的另类解为：

　　h(n)=c(2n,n)-c(2n,n-1)(n=0,1,2,...)

   其前几项为 : 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, ...

 

四、相关问题

1、给定n个数，有多少种出栈序列？

（　　问题的形象描述：

　　　　饭后，姐姐洗碗，妹妹把姐姐洗过的碗一个一个放进碗橱摞成一摞。一共有n个不同的碗，洗前也是摞成一摞的，也许因为小妹贪玩而使碗拿进碗橱不及时，姐姐则把洗过的碗摞在旁边，问：小妹摞起的碗有多少种可能的方式？

　　　　一个有n个1和n个-1组成的字串，且前k个数的和均不小于0，那这种字串的总数为多少？

　　　　P=A1A2A3……An，依据乘法结合律，不改变其顺序，只用括号表示成对的乘积，试问有几种括号化的方案？）
2、n个节点的二叉树有多少种构型？

3、有n+1个叶子的满二叉树的个数？

4、在n*n的格子中，只在下三角行走，每次横或竖走一格，有多少中走法？

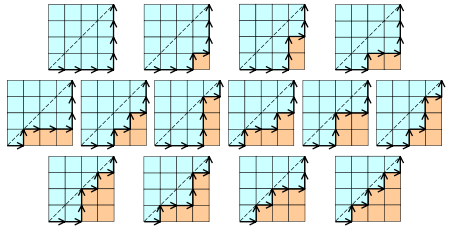
5、将一个凸n+2边形区域分成三角形区域的方法数？

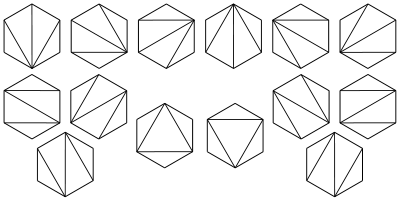
6、在圆上选择2n个点,将这些点成对连接起来使得所得到的n条线段不相交的方法数？

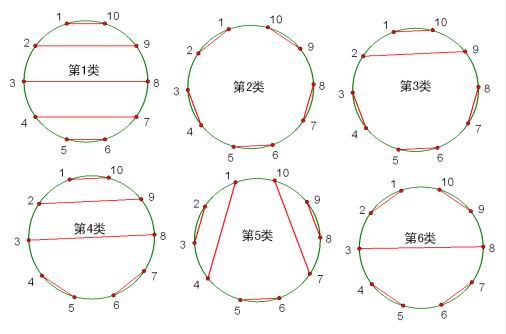
7、n个长方形填充一个高度为n的阶梯状图形的方法个数？

上面一些问题有些是同构的，但有些却实在看不出联系来，他们的答案却都为卡特兰数。