【NOIP2014提高组】解方程

https://www.luogu.org/problem/show?pid=2312

对于30%的数据，n<=2，暴力带入试解。
对于50%的数据，ai很大，结合高精乘法和霍纳算法暴力代入试解。
高精乘法，时间复杂度是很恐怖的而且我不懂写。
注意到虽然ai很大，但是m还是在int范围内的。

继续考虑暴力试解。
考虑到0 mod k=0 (k∈N*)，那么当f(x)=0时，f(x) mod k=0。
但是反过来f(x) mod k=0不一定使f(x)=0成立。当k|f(x)时，f(x) mod k=0也能成立。
为了尽可能避免这种情况，和hash一样，k取几个素数，只有膜这几个素数的时候f(x) mod k=0均成立，才判断f(x)=0成立。

在本题中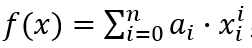，故

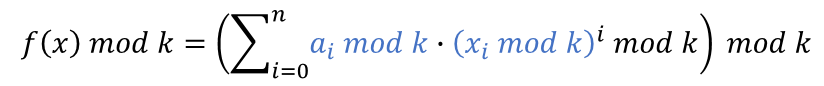
发现ai可以被膜掉，成功回避高精运算。
实际实现的时候可以写一个和快速读入一样的东西，一边读一边膜。也可以先以字符串的形式读进来，再计算成膜k的值。

然后发现xi也被膜掉，也就是说f(x) mod k=f(x+k) mod k。因此试解的时候只需要试[1,k)范围内的解。当然，k要取远比m小的数，这个优化才有意义。

模几个素数呢？模多大的素数呢？这是个非常看脸的问题。少了会WA，多了会TLE。
经过多次测试，模5个10000左右的素数是坠吼的。可是NOIP哪有机会多次测试

#include <algorithm>
#include <iostream>
#include <vector>
#include <cctype>
#include <cstring>
#define maxn 105
#define maxm 1000005
#define NUM_OF_PRIME 5
typedef long long llint;
using namespace std;
const llint prime[NUM_OF_PRIME] = {9859ll, 9631ll, 9059ll, 8783ll, 8291ll};
llint a[maxn][NUM_OF_PRIME]; //a[i][j] => i次项系数 % prime[j]
int n, m;
void geta(int i)
{
    char c;
    bool flag = false;
    while (!isdigit(c = getchar()))
    {
        if (c == '-')
            flag = true;
    }
    do
    {
        for (int k = ; k < NUM_OF_PRIME; k++)
            a[i][k] = (a[i][k] *  % prime[k] + c - '') % prime[k];
    } while (isdigit(c = getchar()));
    if (flag)
    {
        for (int k = ; k < NUM_OF_PRIME; k++)
            a[i][k] = -a[i][k];
    }
}
llint get_val(llint x, int k) // return f(x) mod k
{
    llint val = ;
    for (int i = n; i >= ; i--)
        val = (val * x % prime[k] + a[i][k]) % prime[k];
    return val;
}
bool isroot[maxm];
int main()
{
    cin >> n >> m;
    for (int i = ; i <= n; i++)
        geta(i);
    memset(isroot, true, m + );
    for (int k = ; k < NUM_OF_PRIME; k++)
    {
        for (int i = ; i < min(prime[k], (llint)m + ); i++)
        {
            bool equalzero = get_val(i, k) == ;
            for (int j = i; j <= m; j += prime[k])
                isroot[j] &= equalzero;
        }
    }
    vector<int> ans;
    for (int i = ; i <= m; i++)
        if (isroot[i])
            ans.push_back(i);
    cout << ans.size() << endl;
    for (int i = ; i < ans.size(); i++)
        cout << ans[i] << endl;
    return ;
}