nand flash 扇区的管理以及初始化

（1）首先需要了解NAND FLASH的结构。如图：

以镁光MT29F4G08BxB Nand Flash为例，这款Flash（如上图）以4个扇区（sector）组成1个页（page），64个页(page)组成1个块（block），4096个块(block)构成整个Flash存储器；由于每个扇区的容量是512 字节（bytes)，整个Flash容量为4224M Bit（相当于528M字节），去掉备用区域用于存放ECC数据校验16M（虚线部分），就是这个片子的容量512M字节。其他型号的Flash也是同样由扇区组成页、由页组成块、块组成整个存储设备，只是扇区、页、块的数量多少有区别而已。

在Flash的生产制造过程中，由于生产工艺的缺陷，很容易在Flash中产生不能使用的坏区域，如果在U盘中要使用这样的Flash，就必须使用所谓的“量产工具”；U盘量产工具其实就是一种集坏区域扫描和Flash管理系统装载于一身的工具。常规U盘主控的扫描是以块为单位，扫描即往每一个块里写入数据，然后将读出的数据与写入的数据比较，如果数据有误则把该块标为“坏块”。扫描完成后就是将Flash管理系统装载到Flash里面，Flash管理系统就会利用扫描产生的坏块表对整个Flash进行读写管理，这样就完成了整个量产动作，U盘也就可以正常使用了。所以U盘显示的容量与实际所用的Flash容量差异来源于不能存储信息的坏块和Flash管理系统的占用块。坏块越多，做出的U盘容量越低；而Flash管理系统占用的块是没有办法避免，就像我们的电脑安装操作系统要占用硬盘空间一样。

当然这里还涉及到一个ECC纠错能力的问题，假设对这个Flash进行扫描的定义的ECC纠错能力为1bit，只有数据出现超过1bit错误的块才会被标记为坏块。这个时候需要区分块纠错和扇区纠错的差别，假设任何一个块里有任何一个扇区（512bytes）存在超出1bit的错误，常规主控在扫描的时候就会判断整个块为坏区域，这样将损失整个块128Kbytes的容量；但是当使用扇区纠错的主控时，同样1bit ECC纠错，他会直接去判断这个块里哪些是超出1bit错误的扇区，从而将其剔除，损失的只是每个真正有错误扇区的512bytes容量，从而保留了其余没有错误的扇区，这样Flash的利用率可以得到极大的提高。

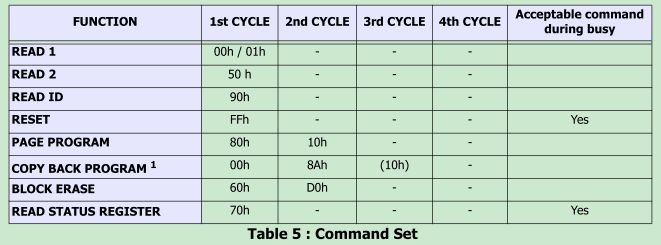
（2） 初始化用的命令序列

（3）NAND的驱动程序

所谓Nand flash的驱动也就是对Nand flash controller编程（发送命令/写寄存器都是同样的意思）。驱动程序的结构大同小异，区别在于每家芯片的Nand flash controller的设计不同，所以对controller的编程的部分是不同的。对于硬件ecc来说，基本的驱动包括下述功能：擦除block、读写page、ecc判断、坏块标识、读取Nand状态、等待Nand、复位Nand、初始化等；初始化中要开辟驱动程序需要的memory，设置工作模式（page大小、block大小、时钟频率、ecc模式等），和对函数指针赋值。

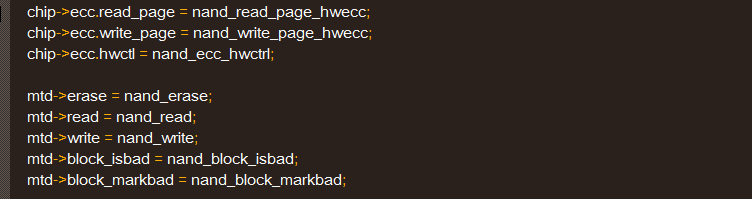
驱动是分层的，以上是最底层的chip的驱动，是为了上层MTD服务的。以读page为例：

chip->cmdfunc(MTD, NAND_CMD_READ0, 0x00, page);//先发读命令，由controller将读命令发给nand flash

chip->ecc.read_page(MTD, chip, buf);//然后读取数据