欧拉工程第63题：Powerful digit counts

题目链接

The 5-digit number, 16807=7⁵, is also a fifth power. Similarly, the 9-digit number, 134217728=8⁹, is a ninth power.

How many n-digit positive integers exist which are also an nth power?

这个题目有点坑：

先说自己的思路<虽然方法不是很好>

根据题意可知道：

a的b次方 除以 最小的b位数（如：1，10,100,1000） 的商 在 1--9之间，则：a的b次方就是符合题意的

然后就根据这个遍历

先找到第一个数符合条件的数firstnum

再找到第一个符合条件之后的第一个不满足条件的数nextnum

则：这中间有 nextnum - firstnum个数

当b也就是次方数大于18的时候，Long都溢出了

此时：有46个数

下面是程序 ：

 package project61;

 import java.math.BigInteger;

 public class P63{
 //    a的b次方是b位数
 //    a的b次方 除以 b位的第一个数（如：1000） 商 在1 - 9之间
 //    以a为开始，找到第一个满足条件的数，如不存在返回 0
 //    满足条件的数是连续的
     long findFirst(long Base,int exp){
         long res =(long) Math.pow(Base, exp);
         long d = 1;
         int Max_Cycle = 10000;
         int texp = exp;
         while(exp!=1){
             d = d*10;
             exp--;
         }
         boolean flag = true ;
         int quot = 0;
         while(Max_Cycle!=0){
             quot = (int) (res/d);
 //            System.out.println(quot+"res:"+res+" Base:"+Base+" d:"+d);
             if(quot>=1 && quot<=9){
                 return Base;
             }
             Base = Base + 1;
             res = (long) Math.pow(Base, texp);
             Max_Cycle--;
         }
         return 0 ;
     }

     long findNext(long Base,int exp){
         long res =(long) Math.pow(Base, exp);
         long d = 1;
         int Max_Cycle = 100000;
         int texp = exp;
         while(exp!=1){
             d = d*10;
             exp--;
         }
         boolean flag = true ;
         int quot = 0;
         while(Max_Cycle!=0){
             quot = (int) (res/d);
             System.out.println("商:"+quot +" 被除数:"+ res+" 除数:"+d+" 底数:"+Base+" 指数:"+texp);
             if(quot==0 ||quot>9){

                 return Base;
             }
             Base = Base + 1;
             res = (long) Math.pow(Base, texp);
             Max_Cycle--;
         }
         return 0 ;
     }
     void run(){
         long result = 0;
         int base = 1;
         int exp = 1;

         while(exp<=18){
             base = 1 ;
             long firstNum = findFirst(base,exp);
             if(firstNum !=0){

             long next = findNext(firstNum,exp);
             System.out.println("第一个满足条件的底数:"+firstNum +" 第一个不满足条件的底数： "+ next);
             result = result + next - firstNum;

             }
             exp++;
         }
         System.out.println(result);
     }

     public static void main(String[] args){
         long begin= System.currentTimeMillis();
         new P63().run();
         long end = System.currentTimeMillis();
         long Time = end - begin;
         System.out.println("Time:"+Time/1000+"s"+Time%1000+"ms");
     }
 }

程序流程：

1.在相同的指数情况小，找符合条件的数

 1.1找到第一个符合条件的数的底数

 1.2找到符合条件数后面的第一个不符合条件的数

 1.3这两个数的差，就是在这个指数下所以符合条件的数

2.增加指数。

下面是运行的结果：

可以看出，只有1-9的底数满足条件，上面红框中的是满足条件后的第一个不满足条件的数。

上面至少知道18，设成18以上，溢出，，，输入上面的46当然是不对的，应该是还有的

尝试直接在9的19,20,21...的数中找符合条件的数：

        BigInteger base = new BigInteger("9");
        BigInteger bigres = new BigInteger("0");
        String toStr = "";
        int exp = 18;

        for(exp=19;exp<25;exp++){
            bigres = base.pow(exp);
            toStr = bigres+"";
            if(toStr.length() ==exp)
            System.out.println(toStr);
        }

通过上面的程序，就只是把符合条件的其他三个数输出了。

答案是：49

上面的过程是不是太复杂了，如果直接利用BigInteger也不会这么复杂的。

然后看到别人是这样做的：

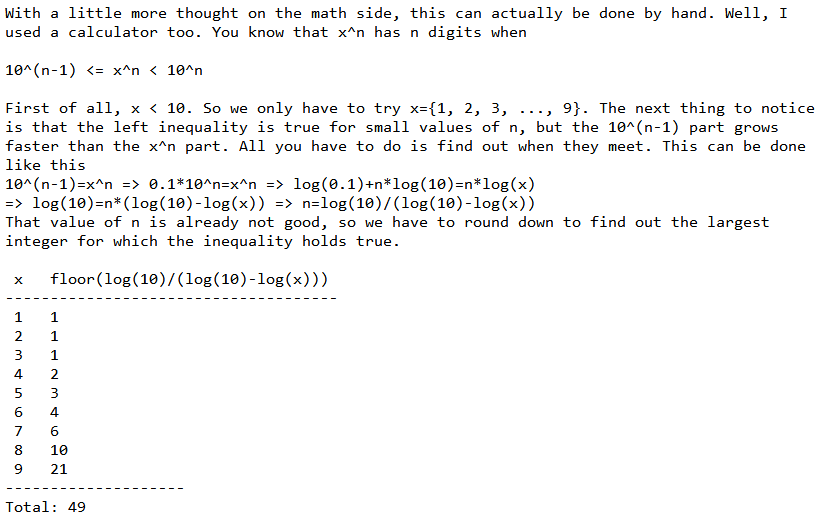
上面说的很详细。。。

void run1(){
        int count = 0;
        for(int x = 1;x<10;x++){
            count +=(int)(1.0/(1-Math.log(x)/Math.log(10)));

        }
        System.out.println(count);
    }

程序就成这样的了。。。

Python程序：

from math import log10

s = 0
for n in range(1,10):
    s += int(1/(1-log10(n)))

print "result=",s 

Python程序就是这样的了。。。

from math import log10

print sum(map(int, map(lambda a: 1.0/(1.0-log10(a)), range(1, 10))))

Python 也可以这样来。。。