【题解】[蓝桥杯] [基础练习VIP]矩形面积交

题目描述

平面上有两个矩形，它们的边平行于直角坐标系的X轴或Y轴。对于每个矩形，我们给出它的一对相对顶点的坐标，请你编程算出两个矩形的交的面积。

输入

输入仅包含两行，每行描述一个矩形。

在每行中，给出矩形的一对相对顶点的坐标，每个点的坐标都用两个绝对值不超过10^7的实数表示。

输出

输出仅包含一个实数，为交的面积，保留到小数后两位。

题解

两个矩形的交就是面积的交，这是属于二维的问题。让我们一步一步出发，先从一维开始推导。(放心，不难^_)

一维线段的交：

让我们在这假设有两条线段，小蓝b和小红r，1,2分别为他们的左右端点。

小蓝由左向右运动，小红由右向左运动。

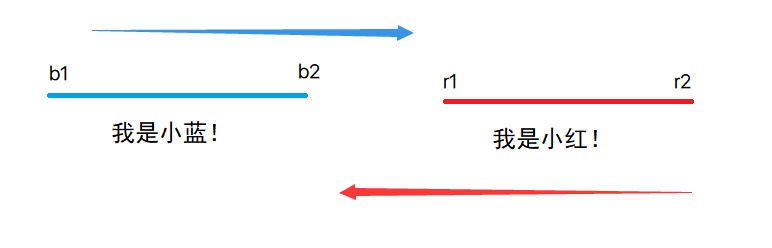
经历阶段

你我永世不见(不相交)

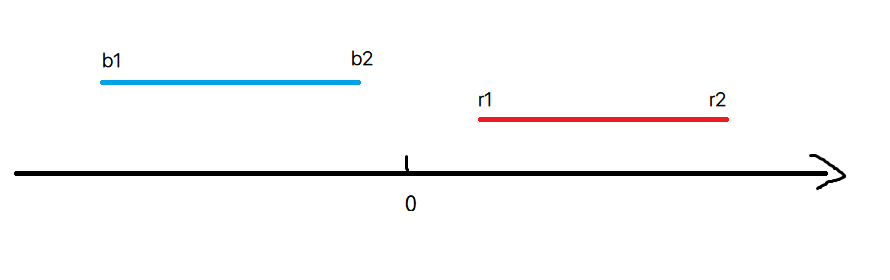
让我们细心观察，发现此时 b2<r1
你我擦肩而过(相交为0)

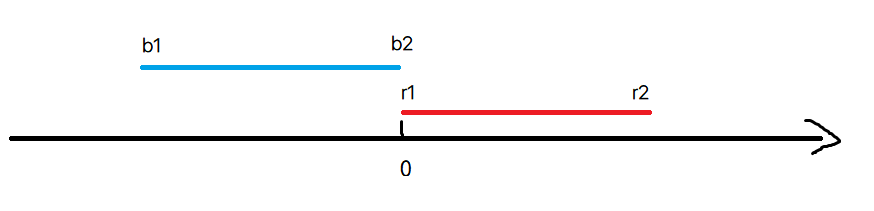
细心观察， b1=r1
你我庆幸相逢(相交)

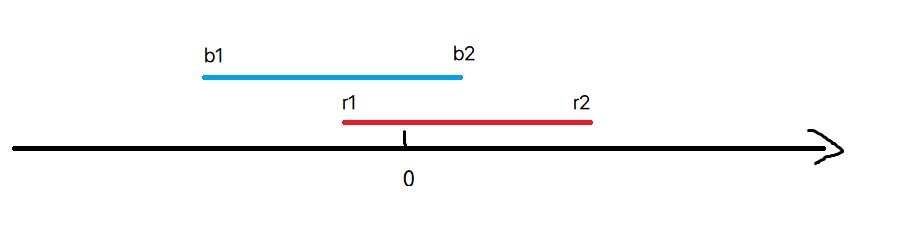
观察可得，b1<r1,b2<r2

但是！由于牵扯到两线段的长短，情况很多，故可根据不相交的区域来间接求得。
你我曲终人散(相交为0)

观察again！r2==b1
你我形同陌路(不相交)

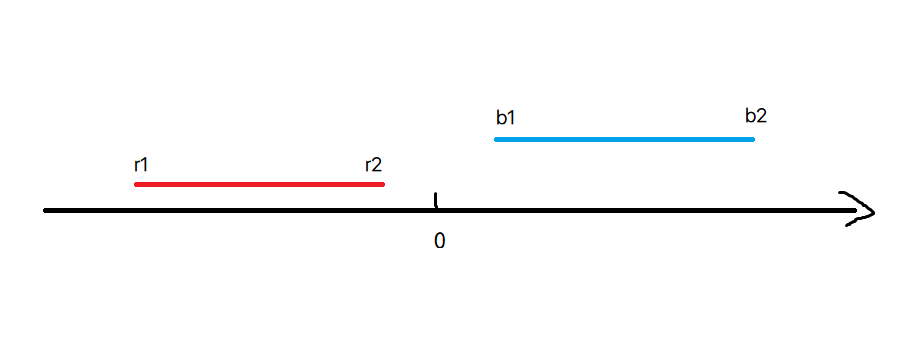
最后一次look！r2<b1

接下来让我们结合以上5种情况：

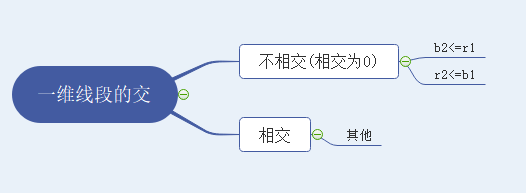
结果不然而喻~

二维矩形求交

让我们请出升级版的小蓝和小红~（长方形和正方形都是矩形哦，这里为了方便，使用的是正方形）

题目输入的是矩形的相对坐标，我们设坐标为分别为

bx1,by1,bx2,by2

rx1,ry1,rx2,ry2

让我们假设他们相交了，进行解题~

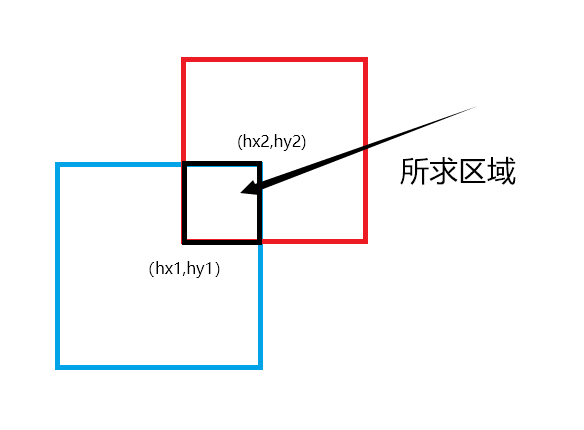
我们设黑色矩形的左下角坐标为(hx1,hy1)，右上角坐标为(hx2,hy2)。

经过细细推敲我发现如下规律：

hx1=max(min(bx1,bx2),min(rx1,rx2))

hy1=max(min(by1,by2),min(ry1,ry2))

hx2=min(max(bx1,bx2),max(rx1,rx2))

hy2=min(max(by1,by2),max(ry1,ry2))

刚看到这些你可能会懵懵的，但是你举几个例子试试看哦！

你会发现数学真奇妙

但是！什么时候才是不相交呢？我们来个不相交的情况你就懂了！

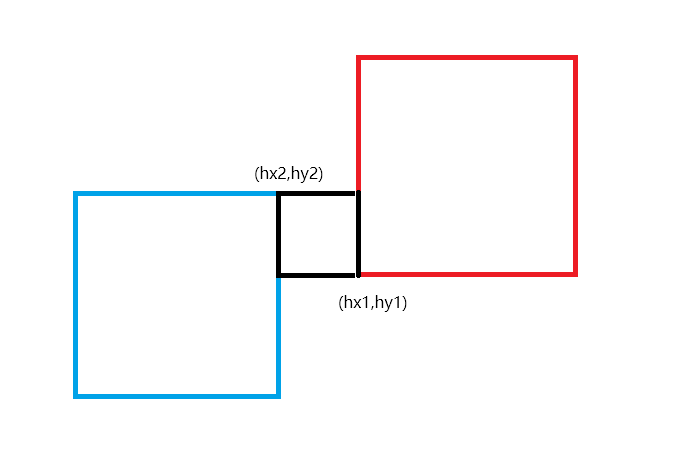
此时你会发现 hx1>hx2,hy1>hy2!

这就不是相交了，于是输出0,00就行了！

经过漫长的图示，终于可以写代码了！废话少说，代码走起！

(我为了创建更少的变量，使用了数组，相信聪明的你一定会看懂的~)

#include <iostream>

#include <cstdio>

#include <cmath>

#define min(x,y) ((x)<(y)?x:y)

#define max(x,y) ((x)>(y)?x:y)

using namespace std;

int main()

{

    double a1[4],a2[4],a3[4],area;

    //输入数据

    for(int i=0;i<4;i++) cin>>a1[i];

    for(int i=0;i<4;i++) cin>>a2[i];

    //计算相交矩形的左下和右上顶点坐标

    a3[0]=max(min(a1[0],a1[2]),min(a2[0],a2[2]));

    a3[1]=max(min(a1[1],a1[3]),min(a2[1],a2[3]));

    a3[2]=min(max(a1[0],a1[2]),max(a2[0],a2[2]));

    a3[3]=min(max(a1[1],a1[3]),max(a2[1],a2[3]));

    if(a3[0]>a3[2]||a3[1]>a3[3]){

        //一定不相交

        printf("0.00");

    } else{

        area = (abs(a3[2]-a3[0])*abs(a3[3]-a3[1]));

        printf("%.2f",area);

    }

    return 0;

}

小提示

C，C++中经过我的查阅，是没有和double类型相对应的max和min函数的，所以，我这里宏定义了一下~

如果你知道有更好的方法可以在下方评论哦！我看到的话一定会回复你的