2023-06-14:我们从二叉树的根节点 root 开始进行深度优先搜索。 在遍历中的每个节点处,我们输出 D 条短划线(其中 D 是该节点的深度) 然后输出该节点的值。(如果节点的深度为 D,则其
2023-06-14:我们从二叉树的根节点 root 开始进行深度优先搜索。
在遍历中的每个节点处,我们输出 D 条短划线(其中 D 是该节点的深度)
然后输出该节点的值。(如果节点的深度为 D,则其直接子节点的深度为 D + 1
根节点的深度为 0
如果节点只有一个子节点,那么保证该子节点为左子节点
给出遍历输出 S,还原树并返回其根节点 root。
输入:"1-2--3--4-5--6--7"。
输出:[1,2,5,3,4,6,7]。
答案2023-06-14:
大体过程如下:
1.根据输入的遍历字符串 S 来构建一个二叉树。
2.定义一个结构体类型 TreeNode,表示二叉树的节点,包括节点值 Val,左子节点 Left,右子节点 Right。
3.定义一个数组 queue,用于存储节点的深度和值。
4.定义两个全局变量 l 和 r,表示队列的左右指针。
5.定义一个函数 recoverFromPreorder,用于根据遍历字符串 S 还原二叉树。
6.遍历字符串 S 的每一个字符:
a.如果该字符不为 '-'(即为数字字符),记录下该数字,直到该数字记录完毕。
b.如果该字符为 '-',则表示该数字已经记录完毕,将该数字加入到 queue 数组中,并将 pickLevel 置为 true。
c.如果该字符是 '-' 或者到达字符串末尾,表示该数字已经记录完毕,将 lvel 记录到队列中, pickLevel 置为 false 。
d.如果该字符是 '-',表示深度加 1;否则,将该数字加入到 number 中。
7.处理掉最后一个数字,将其加入到队列 queue 中。
8.定义一个递归函数 f,用于生成节点,并构建二叉树。
9.取出队列的第一个元素 level,它是当前节点的深度。
10.取出队列的第二个元素 val,它是当前节点的值。
11.生成一个 TreeNode 类型的结构体,元素值为 val,左子节点和右子节点置为 nil。
12.如果队列不为空,且队列的下一个元素的值大于当前节点深度 level,则递归进入左子节点,生成左子树。
13.同样,如果队列不为空,且队列的下一个元素的值大于当前节点深度 level,则递归进入右子节点,生成右子树。
14.返回根节点 head。
时间复杂度为 O(n),其中 n 是遍历字符串 S 的长度。需要遍历字符串 S 一次,并将每个节点入队一次,然后根据队列中的节点数构建二叉树,构建二叉树的时间复杂度也是 O(n)。因此,总时间复杂度为 O(n)。
空间复杂度为 O(n),需要一个数组来存储节点的深度和值,并将其入队。由于二叉树不一定是满二叉树,因此最多需要存储 2n 个节点的深度和值信息。因此,总空间复杂度为 O(n)。
go完整代码如下:
package main
import (
"fmt"
"strconv"
)
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
const MAXN = 2001
var queue [MAXN]int
var l, r int
func recoverFromPreorder(traversal string) *TreeNode {
l = 0
r = 0
number := 0
level := 0
pickLevel := true
for i := 0; i < len(traversal); i++ {
c := traversal[i]
if c != '-' {
if pickLevel {
queue[r] = level
level = 0
r++
pickLevel = false
}
d, _ := strconv.Atoi(string(c))
number = number*10 + d
} else {
if !pickLevel {
queue[r] = number
number = 0
r++
pickLevel = true
}
level++
}
}
queue[r] = number
return f()
}
func f() *TreeNode {
level := queue[l]
head := &TreeNode{Val: queue[l+1], Left: nil, Right: nil}
l += 2
if l < r && queue[l] > level {
head.Left = f()
}
if l < r && queue[l] > level {
head.Right = f()
}
return head
}
func main() {
traversal := "1-2--3--4-5--6--7"
result := recoverFromPreorder(traversal)
fmt.Printf("%+v\n", result)
}
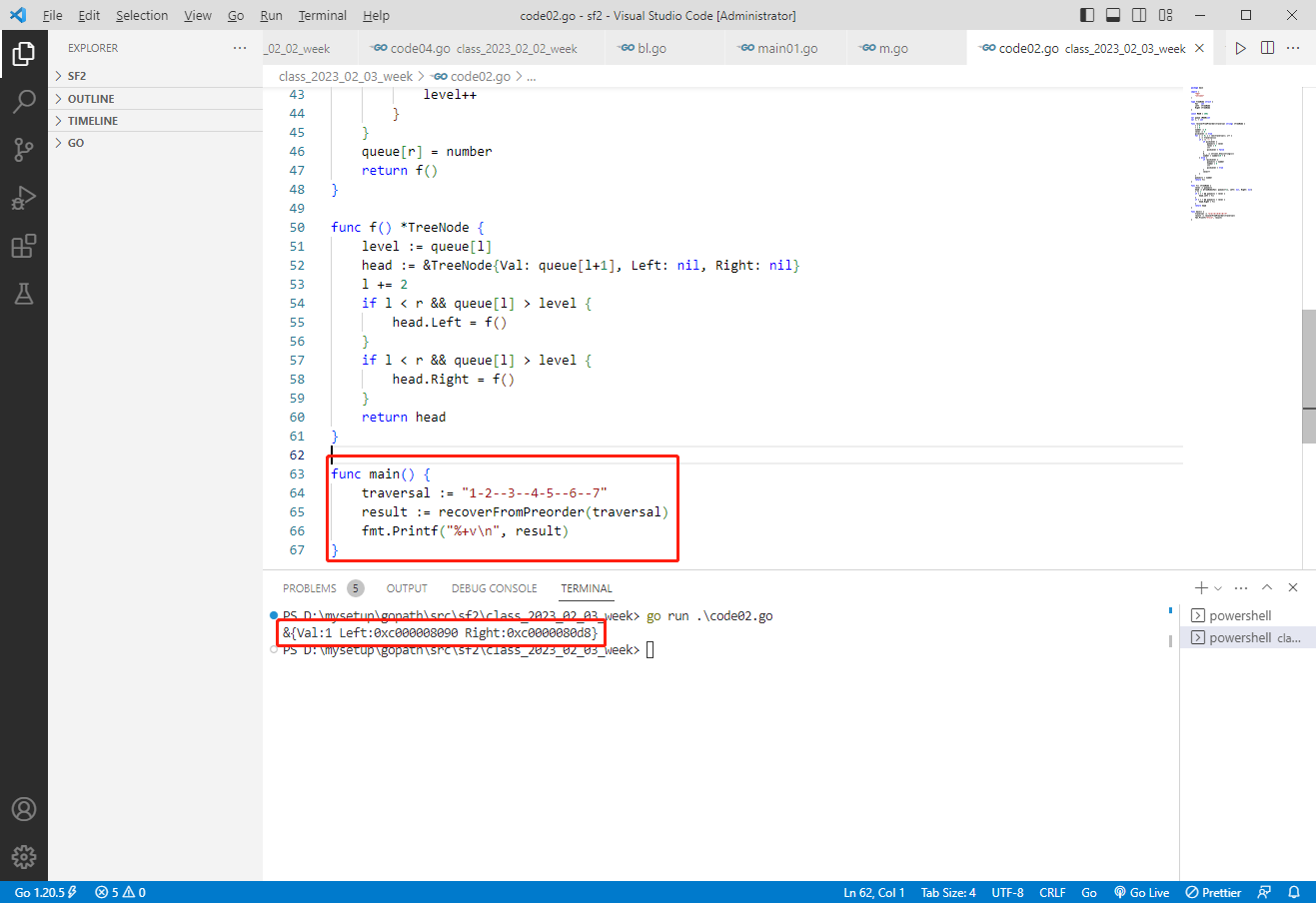
rust完整代码如下:
use std::cell::RefCell;
use std::rc::Rc;
#[derive(Debug, PartialEq, Eq)]
pub struct TreeNode {
pub val: i32,
pub left: Option<Rc<RefCell<TreeNode>>>,
pub right: Option<Rc<RefCell<TreeNode>>>,
}
impl TreeNode {
#[inline]
pub fn new(val: i32) -> Self {
TreeNode {
val,
left: None,
right: None,
}
}
}
fn recover_from_preorder(traversal: String) -> Option<Rc<RefCell<TreeNode>>> {
let mut queue = vec![0; 2001];
let mut l = 0;
let mut r = 0;
let mut number = 0;
let mut level = 0;
let mut pick_level = true;
for c in traversal.chars() {
if c != '-' {
if pick_level {
queue[r] = level;
level = 0;
r += 1;
pick_level = false;
}
number = number * 10 + c.to_digit(10).unwrap() as i32;
} else {
if !pick_level {
queue[r] = number;
number = 0;
r += 1;
pick_level = true;
}
level += 1;
}
}
queue[r] = number;
let queue_len = r + 1;
f(&mut queue, &mut l, queue_len, 0)
}
fn f(queue: &mut [i32], l: &mut usize, r: usize, level: i32) -> Option<Rc<RefCell<TreeNode>>> {
if *l >= r || queue[*l] != level {
None
} else {
*l += 1;
let head = Rc::new(RefCell::new(TreeNode::new(queue[*l])));
*l += 1;
head.borrow_mut().left = f(queue, l, r, level + 1);
head.borrow_mut().right = f(queue, l, r, level + 1);
Some(head)
}
}
fn main() {
let traversal = String::from("1-2--3--4-5--6--7");
let result = recover_from_preorder(traversal);
println!("{:#?}", result);
}
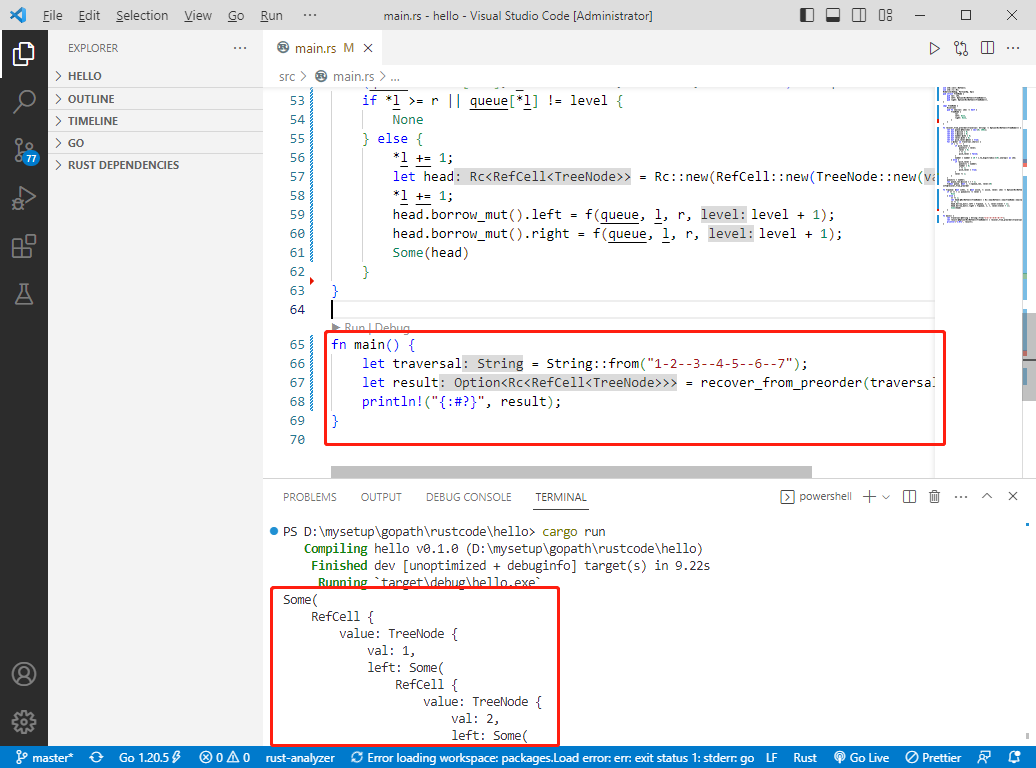
c++完整代码如下:
#include <iostream>
#include <vector>
using namespace std;
struct TreeNode {
int val;
TreeNode* left;
TreeNode* right;
TreeNode() : val(0), left(nullptr), right(nullptr) {}
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
TreeNode(int x, TreeNode* left, TreeNode* right) : val(x), left(left), right(right) {}
};
TreeNode* f();
const int MAXN = 2001;
int queue[MAXN];
int l, r;
TreeNode* recoverFromPreorder(string traversal) {
l = 0;
r = 0;
int number = 0;
int level = 0;
bool pickLevel = true;
for (int i = 0; i < traversal.size(); i++) {
char c = traversal[i];
if (c != '-') {
if (pickLevel) {
queue[r++] = level;
level = 0;
pickLevel = false;
}
number = number * 10 + c - '0';
}
else {
if (!pickLevel) {
queue[r++] = number;
number = 0;
pickLevel = true;
}
level++;
}
}
queue[r++] = number;
return f();
}
TreeNode* f() {
int level = queue[l++];
TreeNode* head = new TreeNode(queue[l++]);
if (l < r && queue[l] > level) {
head->left = f();
}
if (l < r && queue[l] > level) {
head->right = f();
}
return head;
}
int main() {
string traversal = "1-2--3--4-5--6--7";
TreeNode* result = recoverFromPreorder(traversal);
cout << result->val << endl;
cout << result->left->val << endl;
cout << result->right->val << endl;
cout << result->left->left->val << endl;
cout << result->left->right->val << endl;
cout << result->right->left->val << endl;
cout << result->right->right->val << endl;
return 0;
}
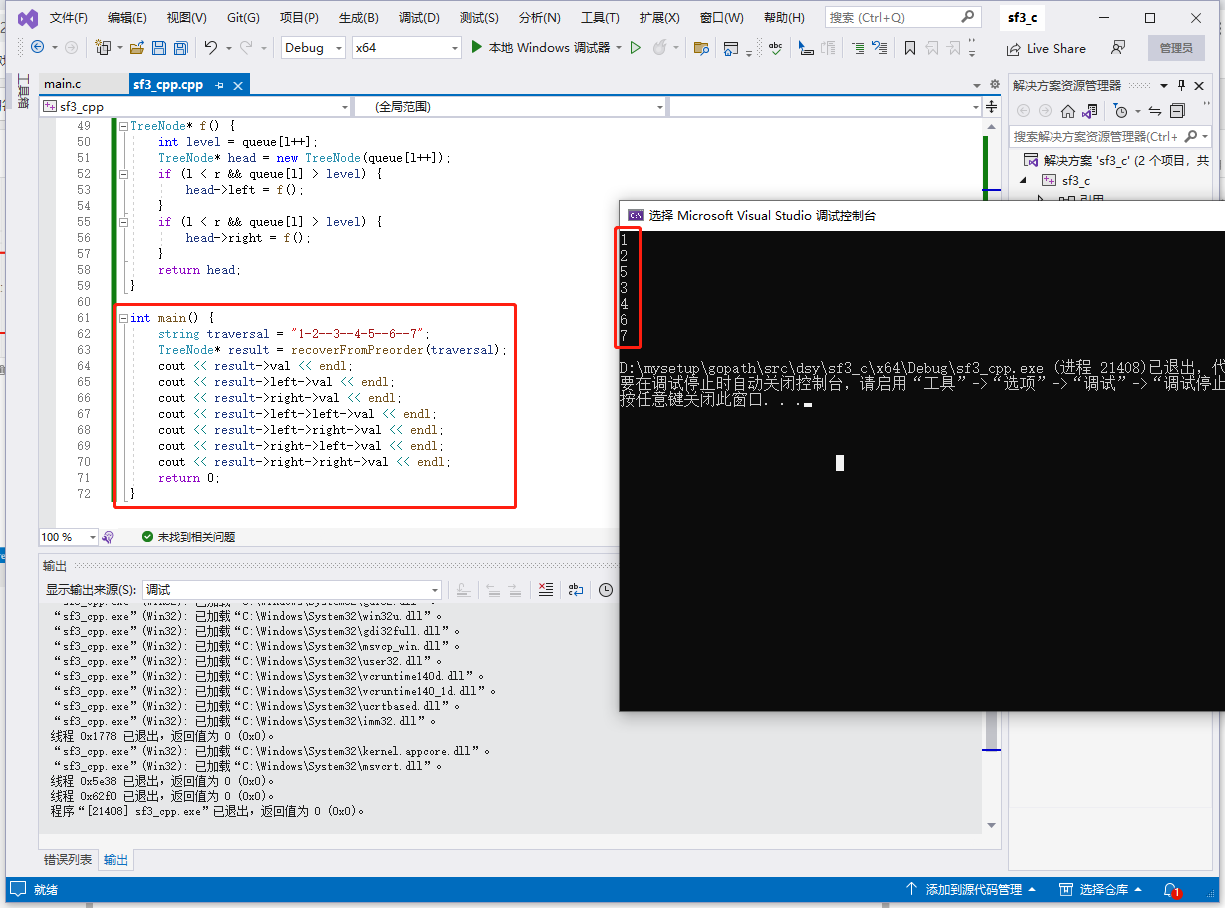
c语言完整代码如下:
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
struct TreeNode {
int val;
struct TreeNode* left;
struct TreeNode* right;
};
struct TreeNode* f();
#define MAXN 2001
int queue[MAXN];
int l, r;
struct TreeNode* recoverFromPreorder(char* traversal) {
l = 0;
r = 0;
int number = 0;
int level = 0;
int pickLevel = 1;
int len = strlen(traversal);
for (int i = 0; i < len; i++) {
char c = traversal[i];
if (c != '-') {
if (pickLevel) {
queue[r++] = level;
level = 0;
pickLevel = 0;
}
number = number * 10 + c - '0';
}
else {
if (!pickLevel) {
queue[r++] = number;
number = 0;
pickLevel = 1;
}
level++;
}
}
queue[r++] = number;
return f();
}
struct TreeNode* f() {
int level = queue[l++];
struct TreeNode* head = (struct TreeNode*)malloc(sizeof(struct TreeNode));
head->val = queue[l++];
head->left = NULL;
head->right = NULL;
if (l < r && queue[l] > level) {
head->left = f();
}
if (l < r && queue[l] > level) {
head->right = f();
}
return head;
}
int main() {
char traversal[] = "1-2--3--4-5--6--7";
struct TreeNode* result = recoverFromPreorder(traversal);
printf("%d\n", result->val);
printf("%d\n", result->left->val);
printf("%d\n", result->right->val);
printf("%d\n", result->left->left->val);
printf("%d\n", result->left->right->val);
printf("%d\n", result->right->left->val);
printf("%d\n", result->right->right->val);
return 0;
}
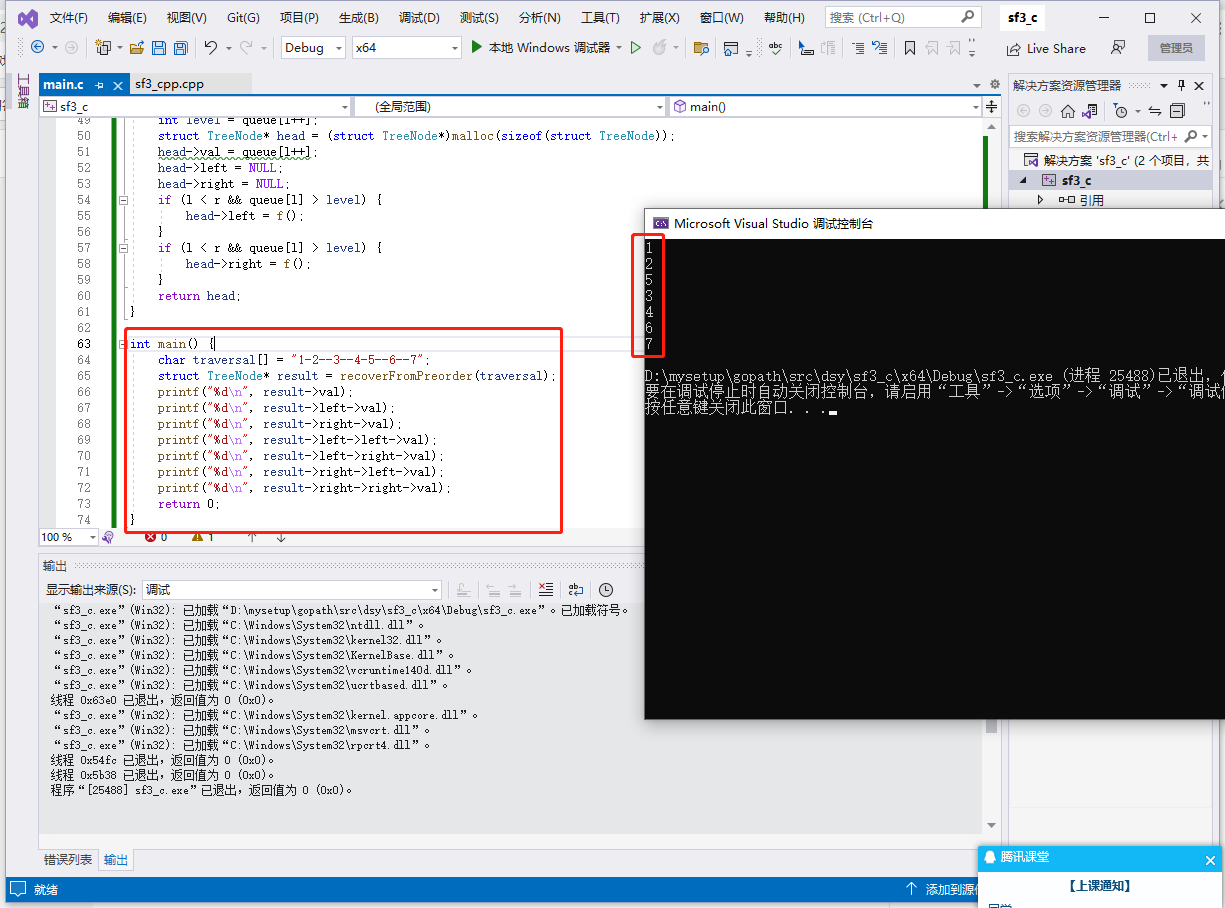
2023-06-14:我们从二叉树的根节点 root 开始进行深度优先搜索。 在遍历中的每个节点处,我们输出 D 条短划线(其中 D 是该节点的深度) 然后输出该节点的值。(如果节点的深度为 D,则其的更多相关文章
- C#图片灰度处理(位深度24→位深度8)、C#图片二值化处理(位深度8→位深度1)
C#图片灰度处理(位深度24→位深度8) #region 灰度处理 /// <summary> /// 将源图像灰度化,并转化为8位灰度图像. /// </summary> / ...
- CF F - Tree with Maximum Cost (树形DP)给出你一颗带点权的树,dist(i, j)的值为节点i到j的距离乘上节点j的权值,让你任意找一个节点v,使得dist(v, i) (1 < i < n)的和最大。输出最大的值。
题目意思: 给出你一颗带点权的树,dist(i, j)的值为节点i到j的距离乘上节点j的权值,让你任意找一个节点v,使得dist(v, i) (1 < i < n)的和最大.输出最大的值. ...
- 二叉树 Java 实现 前序遍历 中序遍历 后序遍历 层级遍历 获取叶节点 宽度 ,高度,队列实现二叉树遍历 求二叉树的最大距离
数据结构中一直对二叉树不是很了解,今天趁着这个时间整理一下 许多实际问题抽象出来的数据结构往往是二叉树的形式,即使是一般的树也能简单地转换为二叉树,而且二叉树的存储结构及其算法都较为简单,因此二叉树显 ...
- Leetcode之深度优先搜索(DFS)专题-129. 求根到叶子节点数字之和(Sum Root to Leaf Numbers)
Leetcode之深度优先搜索(DFS)专题-129. 求根到叶子节点数字之和(Sum Root to Leaf Numbers) 深度优先搜索的解题详细介绍,点击 给定一个二叉树,它的每个结点都存放 ...
- Leetcode之深度优先搜索(DFS)专题-1080. 根到叶路径上的不足节点(Insufficient Nodes in Root to Leaf Paths)
Leetcode之深度优先搜索(DFS)专题-1080. 根到叶路径上的不足节点(Insufficient Nodes in Root to Leaf Paths) 这篇是DFS专题的第一篇,所以我会 ...
- 二叉树系列 - 二叉搜索树 - [LeetCode] 中序遍历中利用 pre节点避免额外空间。题:Recover Binary Search Tree,Validate Binary Search Tree
二叉搜索树是常用的概念,它的定义如下: The left subtree of a node contains only nodes with keys less than the node's ke ...
- http://www.cnblogs.com/huangcong/archive/2010/06/14/1757957.html
http://www.cnblogs.com/huangcong/archive/2010/06/14/1757957.html http://www.cnblogs.com/langtianya/a ...
- httppost的用法(NameValuePair(简单名称值对节点类型)核心对象)
一,案例一 定义了一个list,该list的数据类型是NameValuePair(简单名称值对节点类型),这个代码多处用于Java像url发送Post请求.在发送post请求时用该list来存放参数. ...
- 输出redis cluster 主从的对应关系,如果同一个主从关系的master和slave在同一个node节点上,在输出的对应关系末尾输出提示
需求:输出redis cluster 主从的对应关系,如果同一个主从关系的master和slave在同一个node节点上,在输出的对应关系末尾输出提示. 为什么会有这样的需求呢?在重新搭建redis ...
- Leetcode之深度优先搜索(DFS)专题-513. 找树左下角的值(Find Bottom Left Tree Value)
Leetcode之深度优先搜索(DFS)专题-513. 找树左下角的值(Find Bottom Left Tree Value) 深度优先搜索的解题详细介绍,点击 给定一个二叉树,在树的最后一行找到最 ...
随机推荐
- 念一句咒语 AI 就帮我写一个应用,我人麻了...
原文链接:https://forum.laf.run/d/232 作为人类,我们时常会有自己独特的想法和脑洞大开的创意.然而,这些想法往往因为成本过高而无法实现,毕竟每个人的能力和精力都是有限的,尤其 ...
- [CTF]Caser-Pass-Tool1-C++工具
刷pico遇到一个凯撒密码加密题,顺手写了个解密工具,但是暂时没有解决到边界字母的升降档问题 #include<iostream> using namespace std; int mai ...
- ICMP隐蔽隧道攻击分析与检测(四)
• ICMP隧道攻击通讯特征和特征提取 一.ICMP Ping正常通讯特征总结 一个正常的 ping 每秒最多只会发送两个数据包,而使用 ICMP隧道的服务器在同一时间会产生大量 ICMP 数据包 正 ...
- [云计算]杂谈:SaaS与PaaS的产品经理,做产品设计时有什么区别?[摘]
本文摘自: 郝雨彤@碧岸久 于 2022-09-20在社交平台中所表达的观点. 产品性质/类型 服务领域 服务对象(受众) 核心能力 SaaS 面向具体业务 (所属行业的)业务用户 很看重对业务的理解 ...
- [Excel/Word]常用函数与技巧
1 Excel case1 同时多列筛选 同时筛选多列: 选中首行(属性行)>筛选>(筛选目标的N列) case2 IF/OR/AND/COUNTIF语句 =IF(condition,co ...
- Cesium 案例(九)示例中小程序集合(1)
因为这几天在忙一些客观上无法逃脱的事,没有大块时间对中大型案例进行学习,所以对官方案例中的代码不超过40行的程序进行了学习.我把他们放在一到两个随笔中. 注:[所有案例中最前面务必加上] 1 Cesi ...
- oracle删除一张表后,索引,同义词,视图,约束会被删除么
问题描述:看到有一道题,说删除一张表之后,什么会被关联删除 进行测试,看看一张表什么会被关联删除,进行scoot下的EMP进行测试 一.创建测试需求用例 表结构: SQL> desc emp; ...
- 【Java SE】多线程
1.1 线程的生命周期  方法名 说明 yield() stop() sleep() w ...
- springboot项目 宿舍管理系统 (源码+数据库文件+1w字论文+ppt)
来了就点个赞再走呗,即将毕业的兄弟有福了文章底部获取源码springboot项目 宿舍管理系统 (源码+数据库文件+1w字论文+ppt)技术框架:java+springboot+vue+mysql后端 ...
- JS执行机制--同步与异步
单线程JavaScript语言具有单线程的特点,同一个时间只能做一件事情.这是因为JavaScript脚本语言是为了处理页面中用户的交互,以及操作DOM而诞生的.如果对某个DOM元素进行添加和删除,不 ...
