线性回归 Linear Regression

　　成本函数（cost function）也叫损失函数（loss function），用来定义模型与观测值的误差。模型预测的价格与训练集数据的差异称为残差（residuals）或训练误差（test errors）。

　　我们可以通过残差之和最小化实现最佳拟合，也就是说模型预测的值与训练集的数据最接近就是最佳拟合。对模型的拟合度进行评估的函数称为残差平方和（residual sum of squares）成本函数。就是让所有训练数据与模型的残差的平方之和最小。

　　

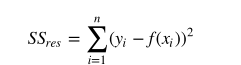
　　我们用R方（r-squared）评估预测的效果。R方也叫确定系数（coefficient of determination），表示模型对现实数据拟合的程度。计算R方的方法有几种。一元线性回归中R方等于皮尔逊积矩相关系数（Pearson product moment correlation coefficient 或Pearson's r）的平方。这种方法计算的R方一定介于0～1之间的正数。其他计算方法，包括scikit-learn中的方法，不是用皮尔逊积矩相关系数的平方计算的，因此当模型拟合效果很差的时候R方会是负值。

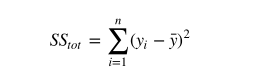
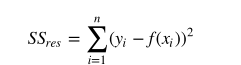
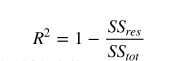
SStot是方差平方和  SSres是残差的平方和

一元线性回归

X_test = [[8], [9], [11], [16], [12]]
y_test = [[11], [8.5], [15], [18], [11]]
model = LinearRegression()
model.fit(X, y)
model.score(X_test, y_test）

score方法计算R方

多元线性回归

最小二乘的代码

from numpy.linalg import lstsq
print(lstsq(X, y)[0])

多项式回归

一种特殊的多元线性回归方法，增加了指数项（x 的次数大于1）。现实世界中的曲线关系都是通过增加多项式实现的，其实现方式和多元线性回归类似。

\(f(x)=\alpha x^2+\beta_1 x+\beta_2\)

多项式 函数PolynomialFeatures

import numpy as np
from sklearn.linear_model import  LinearRegression
from sklearn.preprocessing import PolynomialFeatures

X_train = [[6], [8], [10], [14], [18]]
y_train = [[7], [9], [13], [17.5], [18]]
X_test = [[6], [8], [11], [16]]
y_test = [[8], [12], [15], [18]]
regressor = LinearRegression()
regressor.fit(X_train, y_train)
xx = np.linspace(0, 26, 100)
yy = regressor.predict(xx.reshape(xx.shape[0], 1))
plt = LRplt.runplt()
plt.plot(X_train, y_train, 'k.')
plt.plot(xx, yy)
quadratic_featurizer = PolynomialFeatures(degree=2)
X_train_quadratic = quadratic_featurizer.fit_transform(X_train)
X_test_quadratic = quadratic_featurizer.transform(X_test)
regressor_quadratic = LinearRegression()
regressor_quadratic.fit(X_train_quadratic, y_train)
xx_quadratic = quadratic_featurizer.transform(xx.reshape(xx.shape[0], 1))
plt.plot(xx, regressor_quadratic.predict(xx_quadratic), 'r-')
plt.show()
print(X_train)
print(X_train_quadratic)
print(X_test)
print(X_test_quadratic)
print '一元线性回归 r-squared', regressor.score(X_test, y_test)
print '二次回归 r-squared', regressor_quadratic.score(X_test_quadratic, y_test)

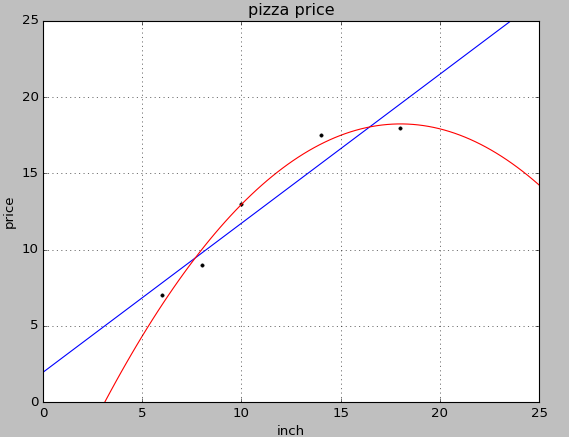
多项式比一次的R值更高，效果好一些。

正则化

正则化（Regularization）是用来防止拟合过度的方法。正则化就是用最简单的模型解释数据。（奥卡姆剃刀原理（Occam's razor））

岭回归（Ridge Regression）岭回归增加L2范数项（相关系数向量平方和的平方根）来调整成本函数（残差平方和）

\(R = \sum_{i=1}^{n} ( y_i - x_i^T \beta)^2 +\lambda \sum_{j=1}^{p}\beta_j^2\)

(L0、L1与L2范数参考)

最小收缩和选择算子(Least absolute shrinkage and selection operator,LASSO)，增加L1范数项（相关系数向量平方和的平方根）来调整成本函数（残差平方和）

\(R=\sum_{i=1}^{n}( y_i - x_i^T \beta)^2 +\lambda\sum_{j=1}^{p}\beta_j\)

LASSO方法会产生稀疏参数，大多数相关系数会变成0，模型只会保留一小部分特征。而岭回归还是会保留大多数尽可能小的相关系数。当两个变量相关时，LASSO方法会让其中一个变量的相关系数会变成0，而岭回归是将两个系数同时缩小。
scikit-learn还提供了弹性网（elastic net）正则化方法，通过线性组合L1和L2兼具LASSO和岭回归的内容。可以认为这两种方法是弹性网正则化的特例。

梯度下降

梯度下降算法是用来评估函数的局部最小值，

可以用梯度下降法来找出成本函数最小的模型参数值。梯度下降法会在每一步走完后，计算对应位置的导数，然后沿着梯度（变化最快的方向）相反的方向前进。总是垂直于等高线。

但是残差平方和的成本函数是个凸函数，梯度下降可以找到全局最小值，而对于部分存在波峰波谷的函数，只能找到局部的。

梯度下降的重要参数（Learning rate）步长小，迭代就小，步长长迭代就大，根据NG的ML公开课推荐的是按照三倍 来缩放步长0.01,0.03,0.1,0.3。

如果按照每次迭代后用于更新模型参数的训练样本数量划分，有两种梯度下降法。批量梯度下降（Batch gradient descent）每次迭代都用所有训练样本。随机梯度下降（Stochastic gradient descent，SGD）每次迭代都用一个训练样本，这个训练样本是随机选择的。当训练样本较多的时候，随机梯度下降法比批量梯度下降法更快找到最优参数。批量梯度下降法一个训练集只能产生一个结果。而SGD每次运行都会产生不同的结果。SGD也可能找不到最小值，因为升级权重的时候只用一个训练样本。它的近似值通常足够接近最小值，尤其是处理残差平方和这类凸函数的时候。

import numpy as np
from sklearn.datasets import load_boston
from sklearn.linear_model import SGDRegressor
from sklearn.cross_validation import cross_val_score
from sklearn.preprocessing import StandardScaler
from sklearn.cross_validation import train_test_split
data = load_boston()
#分割测试集和训练集
X_train, X_test, y_train, y_test = train_test_split(data.data, data.target)
#归一化
X_scaler = StandardScaler()
y_scaler = StandardScaler()

X_train = X_scaler.fit_transform(X_train)
y_train = y_scaler.fit_transform(y_train)
X_test = X_scaler.transform(X_test)
y_test = y_scaler.transform(y_test)

regressor = SGDRegressor(loss='squared_loss')
#交叉验证
scores = cross_val_score(regressor, X_train, y_train, cv=5)
print '交叉验证R方值:', scores
print '交叉验证R方均值:', np.mean(scores)
regressor.fit_transform(X_train, y_train)
print '测试集R方值:', regressor.score(X_test, y_test)