jax框架为例：求hession矩阵时前后向模式的自动求导的性能差别

注意：本文相关基础知识不介绍。

给出代码：

from jax import jacfwd, jacrev
import jax.numpy as jnp
def hessian_1(f):
    return jacfwd(jacrev(f))

def hessian_2(f):
    return jacfwd(jacfwd(f))

def hessian_3(f):
    return jacrev(jacfwd(f))

def hessian_4(f):
    return jacrev(jacrev(f))

def f(x):
    return (x ** 2).sum()

print(hessian_1(f)(jnp.ones((100,))))
print(hessian_2(f)(jnp.ones((100,))))
print(hessian_3(f)(jnp.ones((100,))))
print(hessian_4(f)(jnp.ones((100,))))

import time

a=time.time()
hessian_1(f)(jnp.ones((100,)))
b=time.time()
print(b-a)

hessian_2(f)(jnp.ones((100,)))
c=time.time()
print(c-b)

hessian_3(f)(jnp.ones((100,)))
d=time.time()
print(d-b)

hessian_4(f)(jnp.ones((100,)))
e=time.time()
print(e-d)

运算结果：

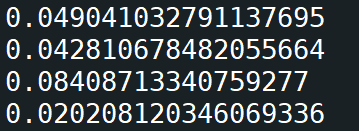
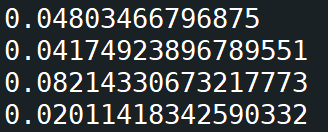
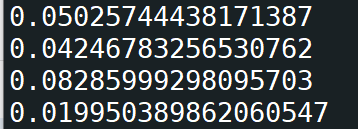
结论（不一定正确）：

两次求导均使用后向模式的要比两次求导均使用前向模式的要速度快，并且两次求导使用相同模式的要比两次求导分别使用不同模式的速度要快；

第一次求导使用后向模式，第二次求导使用前向模式，要比第一次求导使用前向模式，第二次求导使用反向模式的速度要快。

修改代码：

from jax import jacfwd, jacrev
import jax.numpy as jnp
from jax import jit

def hessian_1(f):
    return jacfwd(jacrev(f))

def hessian_2(f):
    return jacfwd(jacfwd(f))

def hessian_3(f):
    return jacrev(jacfwd(f))

def hessian_4(f):
    return jacrev(jacrev(f))

@jit
def f(x):
    return (x ** 2).sum()

x = jnp.ones((100,))

print(hessian_1(f)(x))
print(hessian_2(f)(x))
print(hessian_3(f)(x))
print(hessian_4(f)(x))

import time

a=time.time()
hessian_1(f)(x)
b=time.time()
print(b-a)

hessian_2(f)(x)
c=time.time()
print(c-b)

hessian_3(f)(x)
d=time.time()
print(d-b)

hessian_4(f)(x)
e=time.time()
print(e-d)

运算结果：

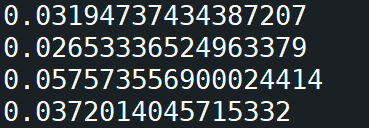
得出另一种结论（之所以上下两次结论不同，个人估计是这个函数太过于简单造成的）：

（不一定正确）

两次求导均使用后向模式的要比两次求导均使用前向模式的要速度慢；

第一次求导使用后向模式，第二次求导使用前向模式，要比第一次求导使用前向模式，第二次求导使用反向模式的速度要快。