Sobel算子 Scharr算子 Laplacian算子

图像梯度处理

• Sobel算子

　　

　　水平方向:

• 对于线条A和线条B，右侧像素值与左侧像素值的差值不为零，因此是边界

　　　上下像素值差值为0，左右素值的差值不为零，分布为正负，

　　　离的近的为2，离的远的为1

　　

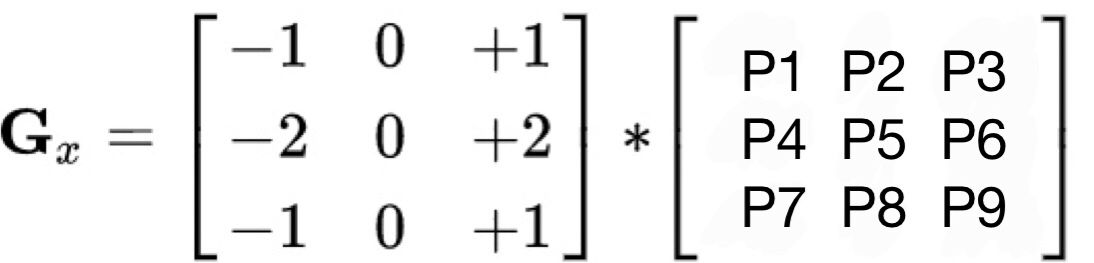
　　　　　　　　　　P5=(P3-P1)+2(P6-P4)+(P9-P7)　　

　　竖直方向：

• 对于线条A和线条B，上侧像素值与下侧像素值的差值不为零，因此是边界

　　　左右像素值差值为0，上下素值的差值不为零，分布为正负，

　　　离的近的为2，离的远的为1

　　　　　　　　　　P5=(P7-P1)+2(P8-P2)+(P9-P3)

　　在使用时，P5可能是负数，所以要取绝对值！

　　cv2.Sobel( src, depth, dx, dy[, ksize[, scale[, delta[, borderType]]]] )

• src表示输入图像

• depth表示输出图像的深度

• dx表示x轴方向的求导阶数

• dy表示y轴方向的求导阶数

  • 注意要分别算x,y轴，不能同时算。同时算不准确

• ksize表示Sobel核的大小

• scale表示计算导数值所采用的缩放因子，默认值是1

• delta表示加在输出图像的值，默认值是0

• borderType表示边界样式

img = cv2.imread('1.jpg',cv2.IMREAD_GRAYSCALE)
#x轴方向的求导阶数
soblex = cv2.Sobel(img,cv2.CV_64F,1,0,ksize=3)
#取绝对值
soblex = cv2.convertScaleAbs(soblex)
#x轴方向的求导阶数
sobley = cv2.Sobel(img,cv2.CV_64F,0,1,ksize=3)
sobley = cv2.convertScaleAbs(sobley)
#x,y轴综合
soblexy = cv2.addWeighted(soblex,0.5,sobley,0.5,0)

#对比，xy同时算
soblexy2 = cv2.Sobel(img,cv2.CV_64F,1,1,ksize=3)
soblexy2 = cv2.convertScaleAbs(soblexy2)

res = np.hstack((img,soblexy,soblexy2))
cv_show('img',res)

• Scharr算子

　　Scharr算子和Sobel算子具有同样速度且精度更高。当Sobel核结构不大时，精度不高，Scharr算子具有更高的精度，Scharr算子是Sobel算子的改进。

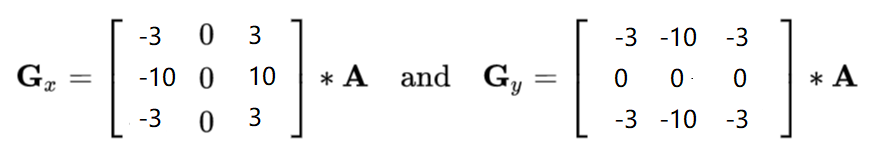
img = cv2.imread('1.jpg',cv2.IMREAD_GRAYSCALE)
scharrx = cv2.Scharr(img,cv2.CV_64F,1,0)
scharrx = cv2.convertScaleAbs(scharrx)
scharry = cv2.Scharr(img,cv2.CV_64F,0,1)
scharry = cv2.convertScaleAbs(scharry)
scharrxy = cv2.addWeighted(scharrx,0.5,scharry,0.5,0)

res = np.hstack((img,scharrxy))
cv_show('img',res)

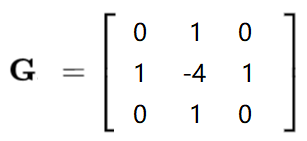
• Laplacian算子

　　Laplacian（拉普拉斯）算子是二阶导数算子，具有旋转不变性，没有边缘的方向信息，双倍加强噪声对图像的影响。通常情况下，Laplacian算子的系数之和为零。

　　Laplacian算子对噪音点敏感！

　　　

　　

　　　　     　　 　　　　

　　　　

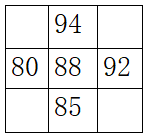
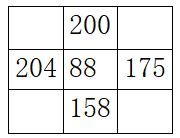
　　　　 •非边界(梯度小，边缘不明显)

　　　　P5=(94+80+92+85)-4x88=-1

　　　　•边界(梯度大，边缘明显)

　　　　P5=(200+204+175+158)-4x88=385

　　　 P5=(20+24+17+15)-4x88=-276

img = cv2.imread('1.jpg',cv2.IMREAD_GRAYSCALE)
laplacian = cv2.Laplacian(img,cv2.CV_64F)
laplacian = cv2.convertScaleAbs(laplacian)

res = np.hstack((img,laplacian))
cv_show('res',res)

　

• Sobel算子 Scharr算子 Laplacian算子对比