使用css实现任意大小，任意方向，任意角度的箭头

网页开发中，经常会使用到下拉箭头，右侧箭头这样的箭头。一般用css来实现：

    {

        display: inline-block;

        margin: 72px;

        border-top: 24px solid;

        border-right: 24px solid;

        width: 120px;

        height: 120px;

        transform: rotate(45deg);

    }

因为这是利用div的border-top, border-right，然后通过旋转div来实现的。

任意角度的箭头

这里有个问题：假如需要一个角度为120度的箭头怎么办呢？由于border-top, border-right一直是90度，所以仅仅通过旋转不行。
我们可以先把div 旋转45度，让它成为一个菱形然后再伸缩，达到任意的角度，这样就可以得到一个任意角度的箭头。由于用到了旋转和伸缩两种变换，所以需要使用
transform: matrix(a,b,c,d,e,f) 这个变换矩阵。这里的6个变量组成了一个3介的变换矩阵

$$
\left[
\begin{matrix}
a & c & e \\
b & d & f \\
0 & 0 & 1
\end{matrix}
\right]
$$

任意点p(x,y)的平移，旋转，伸缩变换以及他们的各种组合都可以通过这个变换矩阵做到：

$$
\left[
\begin{matrix}
x \\
y \\
1
\end{matrix}
\right]
\left[
\begin{matrix}
a & c & e \\
b & d & f \\
0 & 0 & 1
\end{matrix}
\right]=
\left[
\begin{matrix}
x' \\
y' \\
1
\end{matrix}
\right]
$$

注：这里用齐次坐标来表达一个点。简单说就是p(x, y) 表示为p'(x', y', 1)

平移矩阵

v(x, y) 沿着x轴平移tx，沿着y轴平移ty。则有：

x' = x + tx

y' = y + ty

所以平移矩阵：

$$
\left[
\begin{matrix}
x' \\
y' \\
1
\end{matrix}
\right]=
\left[
\begin{matrix}
1 & 0 & tx \\
0 & 1 & ty \\
0 & 0 & 1
\end{matrix}
\right]
\left[
\begin{matrix}
x \\
y \\
1
\end{matrix}
\right]
$$

旋转矩阵

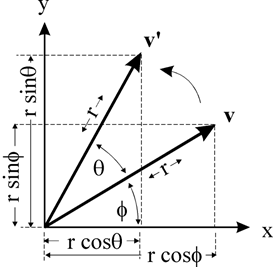
v(x, y) 点绕原点旋转θ到v'(x', y')

则有：

x = r * cos(ϕ )

y = r * sin(ϕ )

x' = r * cos(θ + ϕ) = r * cos(θ) * cos(ϕ) - r * sin(θ) * sin(ϕ ) // 余弦公式

y' = r * sin(θ + ϕ) = r * sin(θ) * cos(ϕ) + r * cos(θ) * sin(ϕ ) // 正弦公式

所以：

x' = x * cos(θ) - y * sin(θ)

y' = x * sin(θ) + y * cos(θ)

所以旋转矩阵：

$$
\left[
\begin{matrix}
x' \\
y' \\
1
\end{matrix}
\right]=
\left[
\begin{matrix}
cos(θ) & -sin(θ) & 0 \\
sin(θ) & cos(θ) & 0 \\
0 & 0 & 1
\end{matrix}
\right]
\left[
\begin{matrix}
x \\
y \\
1
\end{matrix}
\right]
$$

伸缩矩阵

假设x轴，y轴的伸缩率分别是kx， ky。则有：

x' = x * kx

y' = y * ky

所以：

$$
\left[
\begin{matrix}
x' \\
y' \\
1
\end{matrix}
\right]=
\left[
\begin{matrix}
kx & 0 & 0 \\
0 & ky & 0 \\
0 & 0 & 1
\end{matrix}
\right]=
\left[
\begin{matrix}
x \\
y \\
1
\end{matrix}
\right]
$$

复合变换

如果是对p(x, y)先平移(变换矩阵A)，然后旋转(变换矩阵B)，然后伸缩(变换矩阵C)呢?

p' =C(B(Ap)) ==>  p' = (CBA)p //矩阵乘法结合率

现在任意角度o的箭头就很简单了：

先把div旋转45度成为菱形，变换为 M1
伸缩x轴， y轴 :

    x' = size * cos(o/2) = x * √2 *  cos(o/2)

    y' = size * sin(o/2) = y *  √2  * sin(o/2)

即： kx = √2 cos(o/2); ky = √2 sin(o/2)
这样就得到了任意角度的箭头。变换为M2

如果箭头的方向不是指向右侧，在进行一次旋转就可以得到任意方向的箭头。变换为M3

那么由于 p' =C(B(Ap)) ==> p' = (CBA)p, 我们就可以先计算出 M3M2M1，然后对div进行相应的变换，就可以得到任意角度，任意方向的箭头了。

div的width和height就是箭头的边长，通过调整可以获取任意边长的箭头。

React组件

为了方便使用，这个箭头被封装为了一个 React组件。git地址

示例

简单箭头	模拟select	发散箭头

props

name	type	default	description
degree	number	90	箭头的张角, 角度制
offsetDegree	number	0	箭头的方向，默认指向右边
color	string	-	箭头的颜色
size	string	10px	箭头边长

安装使用

npm install rc-arrow --save

import Arrow from 'rc-arrow'

class Hw extends Component {

    render() {

        return (

            <Arrow size="20px" color="red"/>

        )

    }

}