看了还不懂b+tree的本质就来打我

大家好，我是蓝胖子。

今天我们来看看b+tree这种数据结构，我们知道数据库的索引就是由b+tree实现，那么这种结构究竟为什么适合磁盘呢，它又有哪些缺点呢？

我将不会对b+tree的一些定义做过多的讲解，因为这些东西网上一大推，关键还是要抓住本质，想想为什么b+tree这么设计？

b+tree,磁盘，文件系统之间的关系

要想理解b+tree的本质，一定要理解如何在磁盘上高效的存取数据。先看下磁盘是如何读取数据的。

来看下磁盘的结构图。

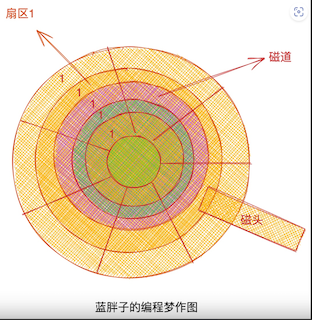
这是磁盘的一个柱面，读数据的时候，就是磁头来回左右的移动。柱面中一圈圈的叫做磁道，每个磁道都被切分为一个个扇区，磁盘读取的单位就是一个扇区一个扇区的读取。而如果要读取的数据在不同的磁道，就需要磁头前后移动到达指定磁道后再移动到特定扇区进行读取，而磁道的变换就是磁盘读取最耗时的过程。

所以对于磁盘怎样加速读取呢？

终极目的要尽量减少存取时不同磁道间的切换，如何减少切换开销？也很简单，往磁盘写入数据时尽可能在同一个磁道上写，从读取读取数据时，也保证尽可能在同一个磁道上读。

但平时我们并不直接操作磁盘，而是通过文件系统往磁盘上写入和读取数据，文件系统每次读取是按块为单位，一个块往往是多个连续的扇区构成。注意连续的扇区是为了减少磁道切换的开销。

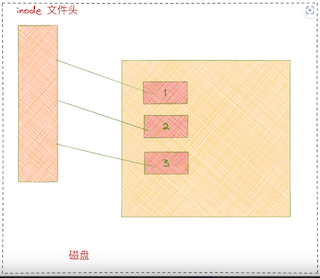
从磁盘上找文件需要找到文件inode数据块，再从inode数据块中找到文件具体的数据块置，可以简单把一个文件理解为一个个文件块构成的，如图每个块都有自己的编号，这里的编号是连续的，实际上，分配的文件块编号也可以不连续。

那么文件系统和b+tree的关系是什么呢？

数据库也是通过文件系统去读取磁盘上的数据的，而数据库中读取数据的单位是一页，不过这个一页数据大小是文件块的整数倍（例如mysql数据页是16kb，而一般操作系统是4kb）。并且数据库实现索引时，会让b+tree中一个节点的大小刚好占用一页数据的大小。

这里其实又会产生一个疑问？如果大小是文件块的整数倍，那么一个btree节点的所占的空间也就是数据库一个数据页所占的空间在磁盘上一定是连续的吗，答案为近乎是连续的，因为文件系统在一次性分配文件块时，为了提升文件系统的性能，即减少磁道的变化，会倾向于连续分配。

比如我们告诉操作系统，往一个文件里写入16kb的数据，那么操作系统为文件分配的这16kb的数据会倾向于由4个连续的文件块构成。

这里还需要特别注意的是，比如文件块1,2,3,4 四个文件块组成b+tree的根节点，那么b+tree的子节点一定是图中的文件块5,6,7,8组成的吗？

实际上也不是，因为随着b+tree节点的删除，分裂等操作，由1,2,3,4文件块组成的根节点指向的子节点位置可能已经变成了其他连续的文件块组成的节点了，它们之间是逻辑上的相邻，在物理磁盘上并不相邻。

举个例子：

为了简单起见，我还是假设数据库在实现的时候，将一个b+tree的节点大小和文件块大小设计为相等。

比如文件块1的节点的左孩子指向了文件块2的节点，如果文件块2的节点中的数据被全部删除了，那么文件块2整个空间就会被标记为删除状态。而文件块1的节点的左孩子指针将会指向其他的文件块，空出来的文件块2的空间则会被新的节点拿来存放数据。可以看到，父子节点之间，只是通过指针联系在了一起，而父子节点可能处于相隔很远的文件块上。

理解了b+tree节点和文件块和磁盘扇区三者关系后，我们再来实际看看b+tree的写入过程，同时便能理解为什么b+tree的写入性能不高了。

b+tree的写入过程

真实数据库的b+tree一个节点能容纳上千个key，为了简单的演示下b+tree的写入过程，这里我会用一个最简单的b+tree来做演示。最简单的b+tree实际上是一颗2-3树。

它具有的特性是每个节点最多能容纳两个元素，孩子节点最多是3个。注意b+tree的插入都是往叶子节点插入。

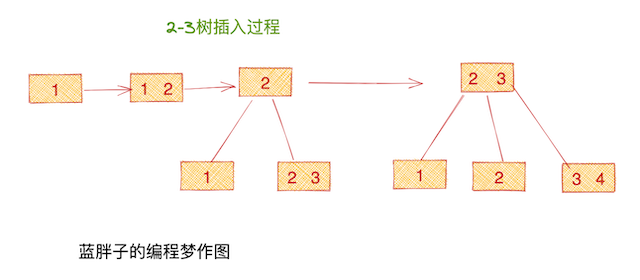
拿最后一个插入元素4举例，首先得从整颗b+tree中找到4应该插入的节点位置，读取节点内容后，发现最后一个叶子节点如果加上元素4，将会破坏2-3树的性质，所以又会产生节点的分裂，其父节点的内容也会发生变化。

由于b+tree各个节点之间在物理磁盘上可能已经跨越了不同的磁道了，所以无论从插入时必须首先得找到节点这个过程来看，还是分裂时会改变父节点这个过程来看，这样的过程都可以认为是随机读写磁盘的行为，都可能跨越多个磁道。而跨越多个磁道的操作，是磁盘最耗时的操作，这样的插入性能当然不高。

后续我也会介绍另一种构建索引的数据结构LSM（日志结构合并树)，有别与b+tree，它具有很好的写入性能。