KNN算法之集美大学

 在本篇文章中，我即将以在集美大学收集到的一些数据集为基础，使用KNN算法进行一系列的操作

一、KNN算法

　　首先，什么是KNN算法呢，这得用到老祖宗说的一句话“近朱者赤近墨者黑”，简单来讲就是，一个物体它靠近什么，我们也可以认为它就是什么。此算法运用广泛，生活中就有体现。比如，你是否发现，你好朋友刷到的抖音视频，你也可能提前刷到过，这就是KNN。

​　　KNN也叫K近邻（K-Nearest Neighbor, KNN）是一种最经典和最简单的有监督学习方法之一。K-近邻算法是最简单的分类器，没有显式的学习过程或训练过程，是懒惰学习（Lazy Learning）。当对数据的分布只有很少或者没有任何先验知识时，K 近邻算法是一个不错的选择。

二、K自制数据集（基于集美大学）

　　集美大学于1918年始建，这所大学的名字很有意思，单纯从字面上看，这是一所集美丽于一身的大学。集美大学也正如名字所说，不仅学校美，周围的环境也跟着美。因为这所大学所在的地区被当地叫做集美学村，这个集美学村是一个旅游区，其中还包含了许多学府，从小学到大学一应俱全，集美大学就在其中，这里给人的感觉很大很美，既适合出行旅游观光，又是学术氛围浓厚之地。在集美大学读书感觉犹如在旅游一般，对于学生来说是一种美好的享受。

　　众所周知，航海是集美大学的特色专业，我运用Excel手动制作了一些数据，内容为航海学院和其他学院的学生数据差异。航海学院纪律严格，判断一个学生是不是航海学院的学子可以从以下角度分析：clothes color（航海学院身穿制度，颜色较为统一），hair length，height。如果是航海学院则nautical college置为1。还有数据三维散点图如下。

　　　　

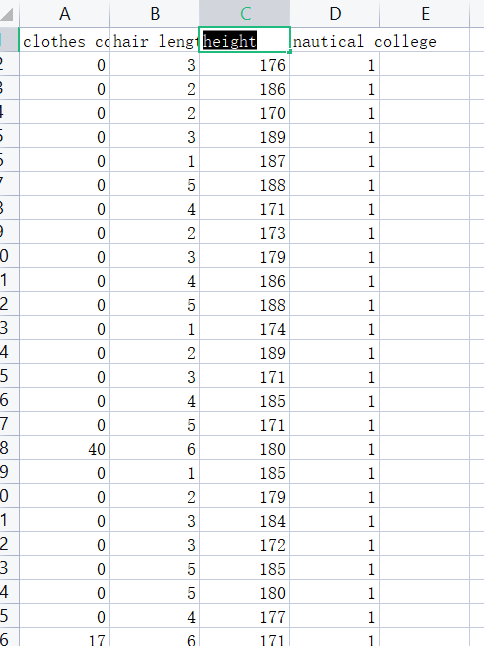
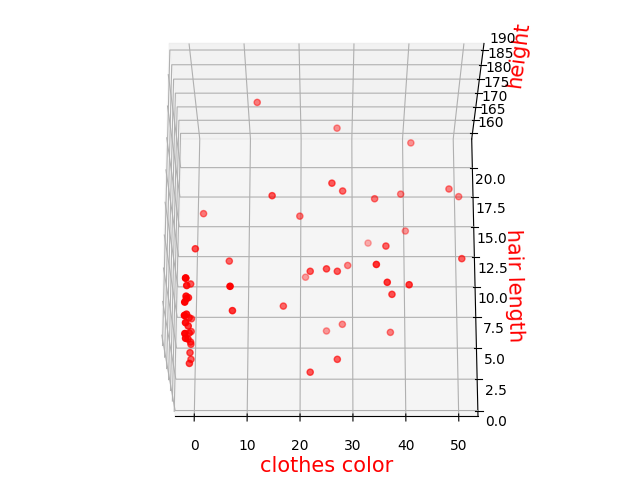
三、代码部分（主要运用了sklearn，pandas工具包）

 1.预测

    file = "sklearn/file/JMU.csv"
    data = pd.read_csv(file)
    lable = data.iloc[:, -1]
    feature = data.iloc[:, :3]
    # 2.划分数据集
    x_train, x_test, y_train, y_test = train_test_split(feature, lable, test_size=0.2)
    #网格搜索和交叉验证
    para_dic={"n_neighbors":[i for i in range(1,20)]}
    estimator=KNeighborsClassifier()
    estimator=GridSearchCV(estimator,param_grid=para_dic)
    estimator.fit(x_train,y_train)
    # 模型评估
    #1.比对真实值与预测值
    # y_pre=estimator.predict(x_test)
    # print("y_pre:\n",y_pre)
    # print(y_pre==y_test)
    #2.计算准确率
    score=estimator.score(x_test,y_test)
    print("准确率：\n",score)

    # 最佳参数
    print("最佳参数：\n",estimator.best_params_)
    # 最佳结果
    print("最佳结果：\n",estimator.best_score_)
    # 最佳估计器
    print("最佳估计器:\n",estimator.best_estimator_)

准确率：
0.9166666666666666
最佳参数：
{'n_neighbors': 1}
最佳结果：
0.8936170212765957
最佳估计器:
KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_jobs=1, n_neighbors=1, p=2,
weights='uniform')

Process finished with exit code 0

2.作图

    x = data.iloc[:, 0]
    y = data.iloc[:, 1]
    z = data.iloc[:, 2]
    # 绘制散点图
    fig = plt.figure()
    ax = Axes3D(fig)
    ax.scatter(x, y, z, color='r')

    # 添加坐标轴(顺序是Z, Y, X)
    ax.set_zlabel('height', fontdict={'size': 15, 'color': 'red'})
    ax.set_ylabel('hair length', fontdict={'size': 15, 'color': 'red'})
    ax.set_xlabel('clothes color', fontdict={'size': 15, 'color': 'red'})
    plt.show()

3.结果分析

通过网格搜索1到20的K值结果可知，最优K取值为1。也就是说找最近的一位同学是否属于航海学院，就能大概率判断这位未知同学是否也为海院学子。

思考，为什么会是K=1呢，通过散点图可以清楚看出，海院学子特征比较集中，所以只要距离海院学子特征最近，就大概率为海院学子。