梯度下降GD,随机梯度下降SGD,小批量梯度下降MBGD

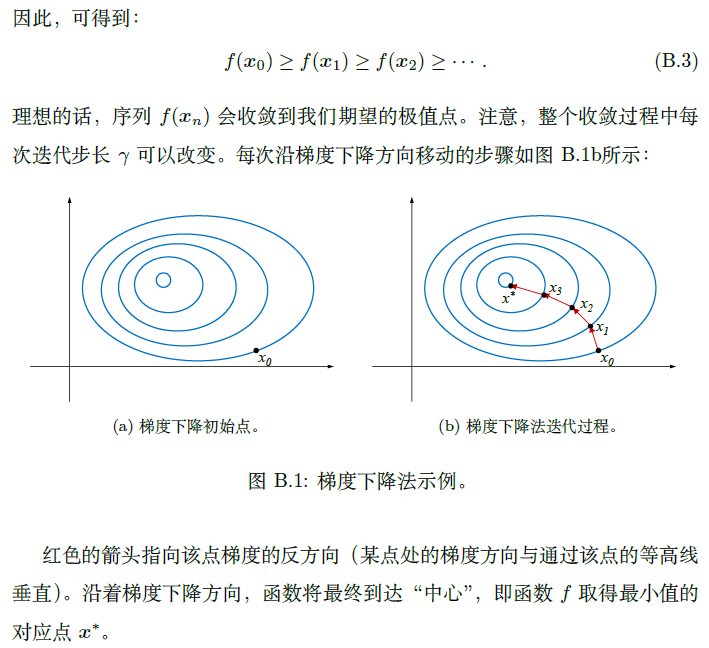



阅读过程中的其他解释:

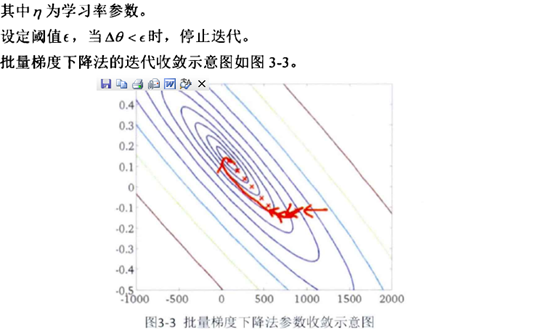


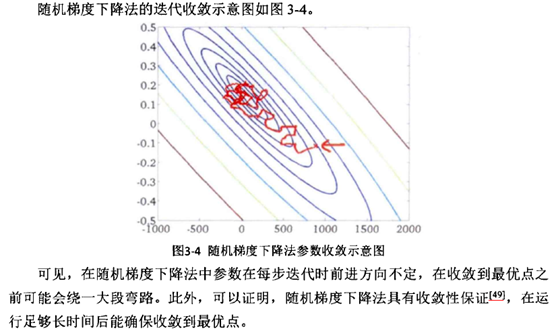


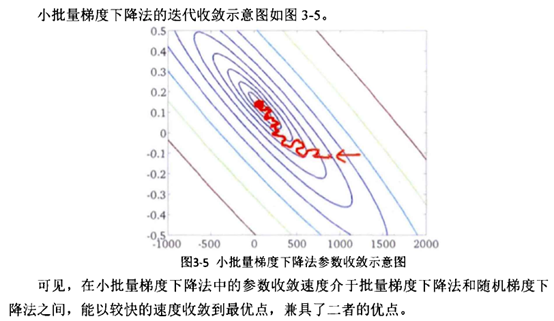

Batch和miniBatch:(广义)离线和在线的不同



梯度下降GD,随机梯度下降SGD,小批量梯度下降MBGD的更多相关文章
- 批量梯度下降(BGD)、随机梯度下降(SGD)以及小批量梯度下降(MBGD)的理解
梯度下降法作为机器学习中较常使用的优化算法,其有着三种不同的形式:批量梯度下降(Batch Gradient Descent).随机梯度下降(Stochastic Gradient Descent ...
- 1. 批量梯度下降法BGD 2. 随机梯度下降法SGD 3. 小批量梯度下降法MBGD
排版也是醉了见原文:http://www.cnblogs.com/maybe2030/p/5089753.html 在应用机器学习算法时,我们通常采用梯度下降法来对采用的算法进行训练.其实,常用的梯度 ...
- L20 梯度下降、随机梯度下降和小批量梯度下降
airfoil4755 下载 链接:https://pan.baidu.com/s/1YEtNjJ0_G9eeH6A6vHXhnA 提取码:dwjq 梯度下降 (Boyd & Vandenbe ...
- 随机梯度下降(Stochastic gradient descent)和 批量梯度下降(Batch gradient descent )的公式对比、实现对比[转]
梯度下降(GD)是最小化风险函数.损失函数的一种常用方法,随机梯度下降和批量梯度下降是两种迭代求解思路,下面从公式和实现的角度对两者进行分析,如有哪个方面写的不对,希望网友纠正. 下面的h(x)是要拟 ...
- 【转】 随机梯度下降(Stochastic gradient descent)和 批量梯度下降(Batch gradient descent )的公式对比、实现对比
梯度下降(GD)是最小化风险函数.损失函数的一种常用方法,随机梯度下降和批量梯度下降是两种迭代求解思路,下面从公式和实现的角度对两者进行分析,如有哪个方面写的不对,希望网友纠正. 下面的h(x)是要拟 ...
- 机器学习-随机梯度下降(Stochastic gradient descent)和 批量梯度下降(Batch gradient descent )
梯度下降(GD)是最小化风险函数.损失函数的一种常用方法,随机梯度下降和批量梯度下降是两种迭代求解思路,下面从公式和实现的角度对两者进行分析,如有哪个方面写的不对,希望网友纠正. 下面的h(x)是要拟 ...
- NN优化方法对照:梯度下降、随机梯度下降和批量梯度下降
1.前言 这几种方法呢都是在求最优解中常常出现的方法,主要是应用迭代的思想来逼近.在梯度下降算法中.都是环绕下面这个式子展开: 当中在上面的式子中hθ(x)代表.输入为x的时候的其当时θ參数下的输出值 ...
- Tensorflow细节-P84-梯度下降与批量梯度下降
1.批量梯度下降 批量梯度下降法是最原始的形式,它是指在每一次迭代时使用所有样本来进行梯度的更新.从数学上理解如下: 对应的目标函数(代价函数)即为: (1)对目标函数求偏导: (2)每次迭代对参数进 ...
- 【深度学习】线性回归(Linear Regression)——原理、均方损失、小批量随机梯度下降
1. 线性回归 回归(regression)问题指一类为一个或多个自变量与因变量之间关系建模的方法,通常用来表示输入和输出之间的关系. 机器学习领域中多数问题都与预测相关,当我们想预测一个数值时,就会 ...
随机推荐
- python3.5上使用virtualenv创建虚拟环境的坑
一.坑一:安装的virtualenv版本太高 显示使用virtualenv 安装虚拟环境报错 出现这个问题就是说明你的virtualev安装的版本太高,降低一下版本重新安装即可,我这里使用的是15这个 ...
- 9.1 Linux存储结构和文件系统
1. 存储结构 Linux系统中的一切文件都是从"根"目录(/)开始的,并按照文件系统层次标准(FHS)采用倒树状结构来存放文件,以及定义了常见目录的用途. 目录名称 应放置文件的 ...
- 【第三课】常用的Linux命令(学习笔记)
4月8日 学习笔记打卡
- nginx从入门到入坟
目录 1.nginx下载安装 2.启动命令 3.服务脚本 4.nginx目录说明 5.nginx配置文件 6.虚拟主机与域名配置和站点配置 6.1server_name配置规则 7.反向代理负载均衡配 ...
- 浅尝Spring注解开发_自定义注册组件、属性赋值、自动装配
Spring注解开发 浅尝Spring注解开发,基于Spring 4.3.12 包含自定义扫描组件.自定义导入组件.手动注册组件.自动注入方法和参数.使用Spring容器底层组件等 配置 @Confi ...
- 配置Linux的时钟同步
公众号关注 「开源Linux」 回复「学习」,有我为您特别筛选的学习资料~ Ubuntu系统默认的时钟同步服务器是ntp.ubuntu.com,Debian则是0.debian.pool.ntp.or ...
- 浅尝Spring注解开发_Servlet3.0与SpringMVC
浅尝Spring注解开发_Servlet 3.0 与 SpringMVC 浅尝Spring注解开发,基于Spring 4.3.12 Servlet3.0新增了注解支持.异步处理,可以省去web.xml ...
- .NET混合开发解决方案14 WebView2的基本身份验证
系列目录 [已更新最新开发文章,点击查看详细] WebView2控件应用详解系列博客 .NET桌面程序集成Web网页开发的十种解决方案 .NET混合开发解决方案1 WebView2简介 .NE ...
- sqlserver limit
select Loaction.Lat,Loaction.Long from Company order by CompanyId OFFSET 4 ROWS FETCH NEXT 2 ROWS ON ...
- 论文解读(GCC)《GCC: Graph Contrastive Coding for Graph Neural Network Pre-Training》
论文信息 论文标题:GCC: Graph Contrastive Coding for Graph Neural Network Pre-Training论文作者:Jiezhong Qiu, Qibi ...
