Navicat Premium 12破解方法
来源网址:https://www.jianshu.com/p/42a33b0dda9c
1、按步骤安装Navicat Premium,如果没有可以去官网下载:http://www.navicat.com.cn/download/navicat-premium
2、安装好后下载激活文件:https://pan.baidu.com/s/1kVgTd6R 提取密码:t1yp
3、下载好后解压文件,可以看到如下目录:
4、选择一个对应的目录下的文件,如我选的是"简单中文64位",复制里面的文件
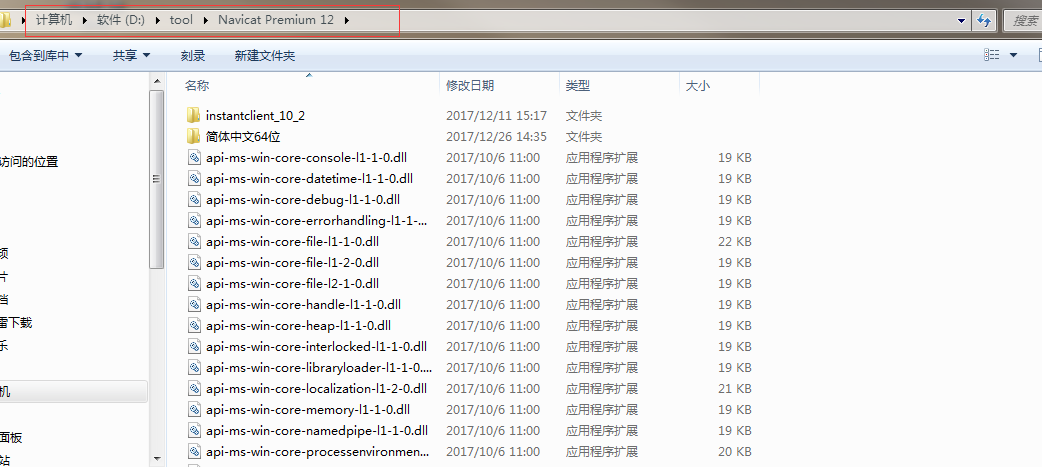
5、找到Navicat Premium 12的安装根目录,将复制的文件粘贴进去即可:
Navicat Premium 12破解方法的更多相关文章
- 【转】Navicat Premium 12破解方法
来源网址:https://www.jianshu.com/p/42a33b0dda9c 1.按步骤安装Navicat Premium,如果没有可以去官网下载:http://www.navicat.co ...
- Navicat Premium 12 破解方法
基本安装下一步下一步,破解方法参考:地址
- Navicat Premium 12破解补丁
Navicat Premium 12破解补丁是专门针对Navicat 12制作的一款破解工具,它可以帮助大家成功激活软件,激活后就可以免费使用软件所有功能了,小编亲测可用,有需要的可以下载试试. Na ...
- Navicat premium 12破解版
下载Navicat Premium 12和破解补丁Navicat_Keygen_Patch,底部有下载地址.下载之后安装Navicat,安装成功后先不要打开,然后打开破解补丁,破解补丁不需要安装,双 ...
- Navicat Premium 12破解激活
下载Navicat Premium 12并安装: 蓝奏云下载:Navicat Premium 12注册机 链接:https://pan.baidu.com/s/1mN-urlh--SX1vbq7h ...
- Navicat Premium 12破解(转载)
一.Navicat Premium 12下载 Navicat Premium 12是一套数据库开发管理工具,支持连接 MySQL.Oracle等多种数据库,可以快速轻松地创建.管理和维护数据库. Na ...
- Navicat Premium 12破解激活11
下载Navicat Premium 12并安装: 百度云下载:Navicat Premium 12注册机 链接:https://pan.baidu.com/s/1UcA5yXjtdfXlBZI-2 ...
- Navicat Premium 12破解版激活(全新注册机)
使用打包下载就可以了 打包下载:(注册机有5.0和5.1用哪个看心情,我用的5.1) 连接:https://pan.baidu.com/s/1ARjFa2vEYxe9sljbrZR8fQ 提取码:lx ...
- Navicat Premium试用期破解方法(转)
转载网址https://blog.csdn.net/Jason_Julie/article/details/82864187 1.按步骤安装Navicat Premium,如果没有可以去官网下载:ht ...
随机推荐
- AngularJS的Scope和Digest
Angular是一个成熟和强大的JavaScript框架.它也是一个比较庞大的框架,在熟练掌握之前,需要领会它提出的很多新概念.很多Web开发人员涌向Angular,有不少人面临同样的障碍.Diges ...
- 从零开始搭建一个从Win7环境备份至CentOS7的SVN双机备份环境
★几个关键的事项★ 需要关闭防火墙filewalld跟selinux ,在root用户下操作: [root@localhost svnRepos]# systemctl stop firewalld ...
- error LNK2001: unresolved external symbol _main
想运行一个网上下载的opengl离屏渲染(渲染到纹理FBO)的程序,然后一直报错 error LNK2001: unresolved external symbol _main 解决了一下午终于弄明白 ...
- 使用git(window)在github上存项目教程
要托管到github,那你就应该要有一个属于你自己的github帐号,所以你应该先到github.com注册 打开浏览器 在地址栏输入地址:github.com 填写用户名.邮箱.密码 点击Sign ...
- IDatabaseInitializer<TContext>接口研究
MSDN官方文档 DropCreateDatabaseIfModelChanges<TContext> 如果实体模型变化,那么重新创建数据库 DropCreateDatabaseAlway ...
- mac 本地跨域
完全退出chrome后终端下输入以下命令: chrome49以前版本 open -a "Google Chrome" --args --disable-web-security c ...
- ionic2 (真正)修改应用图标和启动画面
今天在用ionic2 的ionic resources生成新的icon和splash,生成后安装,应用图标和启动画面依然没变化... 不知道大家有没有被坑过,今天被坑了一下午,终于找到了办法: 解决方 ...
- 180400之pycharm快捷方式汇总
1.Pycharm中快捷键大全,遇到一个更新一个 撤销与反撤销:Ctrl + z,Ctrl + Shift + z 缩进.不缩进:Tab.Shift + tab 运行:Shift + F10 批量注释 ...
- oracle 存储过程调用方式
Oracle存储过程包含三部分:过程声明,执行过程部分,存储过程异常. Oracle存储过程可以有无参数存储过程和带参数存储过程. 一.无参程序过程语法 1 create or replace pro ...
- django之Ajax初识
Ajax准么说是用于Javascript与服务器端进行交互的,我们之前呢没有了解ajax也同样可以完成与服务器的交互,那么ajax的优势在哪里?首先ajax是异步交互的也就是说我们基本不会遇到卡顿现象 ...