图->最短路径->多源最短路径(弗洛伊德算法Floyd)

文字描述

　　求每一对顶点间的最短路径，可以每次以一个顶点为源点，重复执行迪杰斯特拉算法n次。这样，便可求得每一对顶点之间的最短路径。总的执行时间为n^3。但是还有另外一种求每一对顶点间最短路径的方法，就是弗洛伊德(Floyd)算法，它的时间复杂度也为n^3,但是形式上更简单，其基本思想如下：

　　

　　如果无法理解上面的文字的话，建议看下代码实现部分，可以更容易理解。

示意图

　

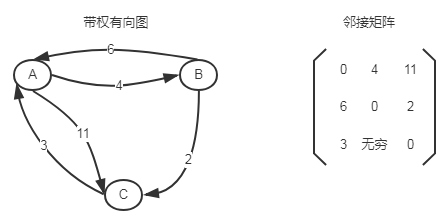
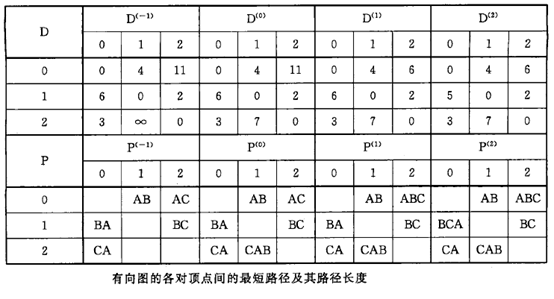
算法分析

时间复杂度为n^3

代码实现

 //
 // Created by lady on 19-1-6.
 //

 #include <stdlib.h>
 #include <stdio.h>
 #include <string.h>

 #define INFINITY        100000    //最大值
 #define MAX_VERTEX_NUM    20        //最大顶点数

 typedef enum {DG, DN, UDG, UDN} GraphKind; //{有向图，有向网，无向图，无向网}
 typedef struct ArcCell{
     int weight;    //该弧相关信息的指针
 }ArcCell, AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM], PathMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
 typedef struct VertexType{
     char data[];
 }VertexType;
 typedef struct{
     VertexType vexs[MAX_VERTEX_NUM];    //顶点向量
     AdjMatrix arcs;        //邻接矩阵
     int vexnum, arcnum;    //图的当前顶点数和弧数
     GraphKind kind;        //图的种类标志
 }MGraph;

 /*
  * 根据顶点信息， 返回该顶点在图中的位置， 如果返回-1表示顶点不存在
  */
 static int LocateVex(MGraph *G, char data[])
 {
     int i = ;
     for(i=; i<G->vexnum; i++){
         if(!strncmp(G->vexs[i].data, data, strlen(G->vexs[i].data))){
             return i;
         }
     }
     return -;
 }

 /*
  * 用邻接矩阵作为存储结构，创建有向网
  */
 static int CreateGraphDN(MGraph *G)
 {
     printf("用邻接矩阵创建有向网,输入顶点数，弧数：");
     G->kind = DN;
     scanf("%d,%d", &G->vexnum, &G->arcnum);
     if(G->vexnum > MAX_VERTEX_NUM){
         printf("错误:顶点数不能超过%d!!\n", MAX_VERTEX_NUM);
         return -;
     }
     int i = , j = , k = ;
     char v1[] = {}, v2[]={}, info[] = {};
     char tmp[] = {};
     for(i=; i<G->vexnum; i++){
         printf("输入第%d个顶点: ", i);
         memset(G->vexs[i].data, , sizeof(G->vexs[].data));
         scanf("%s", G->vexs[i].data);
         for(j=; j<G->vexnum; j++){
             G->arcs[i][j].weight = INFINITY;
         }
         G->arcs[i][i].weight = ;
     }
     for(k=; k<G->arcnum; k++){
         printf("输入第%d条弧(顶点1, 顶点2, 权值): ", k);
         memset(tmp, , sizeof(tmp));
         scanf("%s", tmp);
         sscanf(tmp, "%[^','],%[^','],%s[^\\n]", v1, v2, info);
         i = LocateVex(G, v1);
         j = LocateVex(G, v2);
         if(i< || j< || (!atoi(info))){
             printf("错误:顶点%s或者%s不存在, 或者权值信息%s不对!\n", v1, v2, info);
             return -;
         }
         G->arcs[i][j].weight = atoi(info);
     }
     return ;
 }

 static void printMatrix(int vexnum, VertexType vexs[], int (*arcs)[MAX_VERTEX_NUM])
 {
     int i = , j = ;
     printf("\t");
     for(i=; i<vexnum; i++){
         printf("%s\t", vexs[i].data);
     }
     printf("\n");
     for(i=; i<vexnum; i++){
         printf("%s\t", vexs[i].data);
         for(j=; j<vexnum; j++){
             if(arcs[i][j] == INFINITY){
                 printf("INF\t");
             }else{
                 printf("%d\t", arcs[i][j]);
             }
         }
         printf("\n");
     }
     return ;
 }
 static void printArchs(int vexnum, VertexType vexs[], AdjMatrix arcs)
 {
     int i = , j = ;
     printf("\t");
     for(i=; i<vexnum; i++){
         printf("%s\t", vexs[i].data);
     }
     printf("\n");
     for(i=; i<vexnum; i++){
         printf("%s\t", vexs[i].data);
         for(j=; j<vexnum; j++){
             if(arcs[i][j].weight == INFINITY){
                 printf("INF\t");
             }else{
                 printf("%d\t", arcs[i][j].weight);
             }
         }
         printf("\n");
     }
     return ;
 }

 /*
  * 用Floyd算法求有向图G中各顶点v和w之间的最短路径P[v][w]及其
  * 带权长度D[v][w]。若P[v][w][u]为1, 则u为从v到w当前求得最短路径上的顶点。
  */
 void ShortestPath_Floyd(MGraph *G)
 {
     int u=, v=, w=;
     int i=, j=;
     int P[MAX_VERTEX_NUM][MAX_VERTEX_NUM][MAX_VERTEX_NUM];
     int D[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
     //各对结点之间初始已知路径和距离
     for(v=; v<G->vexnum; v++){
         for(w=; w<G->vexnum; w++){
             D[v][w] = G->arcs[v][w].weight;
             for(u=; u<G->vexnum; u++){
                 P[v][w][u] = ;
             }
             //从v到w有直接路径
             if(D[v][w] < INFINITY){
                 P[v][w][v] = ;
                 P[v][w][w] = ;
             }
         }
     }

     for(u=; u<G->vexnum; u++){
         for(v=; v<G->vexnum; v++){
             for(w=; w<G->vexnum; w++){
                 if( D[v][u]+D[u][w] < D[v][w]){
                     //从v经u到w的一条路径更短。
                     D[v][w] = D[v][u] + D[u][w];
                     for(i=; i<G->vexnum; i++){
                         P[v][w][i] = (P[v][u][i] || P[u][w][i]) ? : ;
                     }
                 }
             }
         }
     }

     printf("\n打印各个顶点间的最短路径的权值:\n");
     printMatrix(G->vexnum, G->vexs, D);

     printf("\n打印各个顶点间的最短路径的中间结点:\n");
     for(u=; u<G->vexnum; u++){
         for(v=; v<G->vexnum; v++){
             printf("minpath(%d,%s<->%d,%s):", u, G->vexs[u].data, v, G->vexs[v].data);
             for(w=; w<G->vexnum; w++){
                 if(P[u][v][w] && (u!=v)){
                     printf("%s\t", G->vexs[w].data);
                 }
             }
             printf("\n");
         }
     }

     return ;
 }

 int main(int argc, int *argv[])
 {
     //以邻接矩阵为存储结构创建有向网
     MGraph G;
     if(CreateGraphDN(&G) < ){
         return -;
     }
     printf("\n打印该图中的信息:\n");
     printArchs(G.vexnum, G.vexs, G.arcs);
     //Floyd弗洛依德算法求多源最短路径
     ShortestPath_Floyd(&G);
 }

弗洛依德算法(Floyd)求多源最短路径

代码运行

/home/lady/CLionProjects/untitled/cmake-build-debug/untitled
用邻接矩阵创建有向网,输入顶点数，弧数：,
输入第0个顶点: A
输入第1个顶点: B
输入第2个顶点: C
输入第0条弧(顶点1, 顶点2, 权值): A,B,
输入第1条弧(顶点1, 顶点2, 权值): B,A,
输入第2条弧(顶点1, 顶点2, 权值): A,C,
输入第3条弧(顶点1, 顶点2, 权值): C,A,
输入第4条弧(顶点1, 顶点2, 权值): B,C,

打印该图中的信息:
    A    B    C
A
B
C        INF        

打印各个顶点间的最短路径的权值:
    A    B    C
A
B
C                

打印各个顶点间的最短路径的中间结点:
minpath(,A<->,A):
minpath(,A<->,B):A    B
minpath(,A<->,C):A    B    C
minpath(,B<->,A):A    B    C
minpath(,B<->,B):
minpath(,B<->,C):B    C
minpath(,C<->,A):A    C
minpath(,C<->,B):A    B    C
minpath(,C<->,C):

Process finished with exit code