BZOJ5416 NOI2018冒泡排序（动态规划+组合数学）

　　打表可以发现相当于不存在长度>=3的递减子序列。

　　考虑枚举在哪一位第一次不卡限制。注意到该位一定会作为前缀最大值。判掉已确定位不合法的情况后，现在的问题即为求长度为i、首位>j的合法排列个数，设其为g[i][j]。

　　由于首位>j，1~j在排列中一定依次出现，并且在j出现之前，>j的部分也一定单增。于是可以先将>j的部分安排好，再将1~j不改变相对顺序地插入。>j的部分即是考虑没有各种奇怪的限制要怎么求。设f[i][j]为长度i的排列，第一个非前缀max的数在j位置的方案数。特别地，令f[i][i+1]为不存在这样的数时的方案数（当然就是1）。则有f[i][j]=Σf[i-1][k] (j-1<=k<=i+1)，也即f[i][j]=f[i][j+1]+f[i-1][j-1]。这样f[i][1~i+1]即为n=i且无限制的答案，并且有了这个求g就很容易了，即考虑1~j的插入位置，有g[i][j]=Σf[i-j][k]·C(j+k-2,k-2) (k=2~i-j+1)。于是得到了一个80分的做法。给无限制时的答案打一下表又可以发现答案即为卡特兰数，可以再拿4分。

　　似乎有点陷入僵局。继续打表！我们惊奇的发现，g[i][j]=f[i+1][j+3]。这个式子可能是说明之前绕了太多弯，本来直接考虑怎么推g就行了，虽然这个我没想清楚也懒得考虑了。由于最终要用到的只是g中的n项，如果能快速求出f数组中任意项，问题就解决了。

　　考虑根据f的转移方程画一张有向图，答案即为由原点走到目标点的路径条数。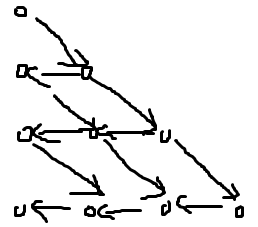

得到这样一个丑陋的图。如果要到最左的点，就是卡特兰数的经典模型。于是下面所有的分析只要类比卡特兰数就可以了。事实上这是个原题https://www.luogu.org/problemnew/show/P1641。

　　考虑先不管图的边界随便走，此时向右下走n步、向左走m步时的方案数显然是C(n+m,m)。加上边界后，考虑哪些走法会变得不合法，显然不合法的方案中一定存在一个第一次跨过边界的点，而这可以看做是从左上一个并不存在的点（原点向左平移两格）、以边界为对称轴、按和右边对称的走法走来的，经过此点后走法变为和右边相同。并且显然每一种从这个不存在的点到达终点的走法都对应于一种不合法方案。两个组合数相减即可。原问题也被线性解决了。

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
#define ll long long
#define P 998244353
#define N 600010
char getc(){char c=getchar();while ((c<'A'||c>'Z')&&(c<'a'||c>'z')&&(c<''||c>'')) c=getchar();return c;}
int gcd(int n,int m){return m==?n:gcd(m,n%m);}
int read()
{
    int x=,f=;char c=getchar();
    while (c<''||c>'') {if (c=='-') f=-;c=getchar();}
    while (c>=''&&c<='') x=(x<<)+(x<<)+(c^),c=getchar();
    return x*f;
}
int T,n,a[N],fac[N<<],inv[N<<],mn[N],ans;
int C(int n,int m){if (m<) return ;return 1ll*fac[n]*inv[m]%P*inv[n-m]%P;}
int calc(int n,int m){m=n-m;return (C(n+m,m)-C(n+m,m-)+P)%P;}
int main()
{
#ifndef ONLINE_JUDGE
    freopen("bzoj5416.in","r",stdin);
    freopen("bzoj5416.out","w",stdout);
    const char LL[]="%I64d\n";
#else
    const char LL[]="%lld\n";
#endif
    T=read();
    while (T--)
    {
        n=read();
        for (int i=;i<=n;i++) a[i]=read();
        fac[]=;for (int i=;i<=*n;i++) fac[i]=1ll*fac[i-]*i%P;
        inv[]=inv[]=;for (int i=;i<=*n;i++) inv[i]=P-1ll*(P/i)*inv[P%i]%P;
        for (int i=;i<=*n;i++) inv[i]=1ll*inv[i-]*inv[i]%P;
        int mx=;ans=;
        mn[n+]=n+;
        for (int i=n;i>=;i--) mn[i]=min(mn[i+],a[i]);
        for (int i=;i<=n;i++)
        {
            mx=max(mx,a[i]);
            ans=(ans+calc(n-i+,mx-i+))%P;
            if (a[i]<mx&&a[i]>mn[i+]) break;
        }
        printf("%d\n",ans);
    }
    return ;
}