Pi Zero三代版本演化比较

本文介绍Pi Zero的版本演进.

5美元的Pi Zero一上市即造成轰动！

2015年11月树莓派基金会发表了只有5美元的树莓派计算机：PiZero，且只要购买纸本的第40期MagPi杂志就可以附送一片，一时间造成喧腾，甚至出现网络上转手再卖的Pi Zero，价格高达20倍100美元。

不过随着热潮过去，大家逐渐恢复理智，Pi Zero依然是比其他20～35美元的树莓派低阶低规。即便如此，在一些非常初阶的应用上，Pi Zero仍相当合适。

(树莓派的官方网站上有相关的介绍视频)

Pi Zero从1.2版起跳，只收5美元

根据笔者观察，Pi Zero一推出时，它的印刷电路板（PCB）布局设计就已经是1.2版，几乎找不着有关1.0、1.1版的数据，有兴趣的读者，可以到此网址下载与了解Pi Zero 1.2版的电路设计。

不过这个网址只有等效电路图，而非线路布局图，还有这个网址可以观看1.2版的机械外观设计，如下图。

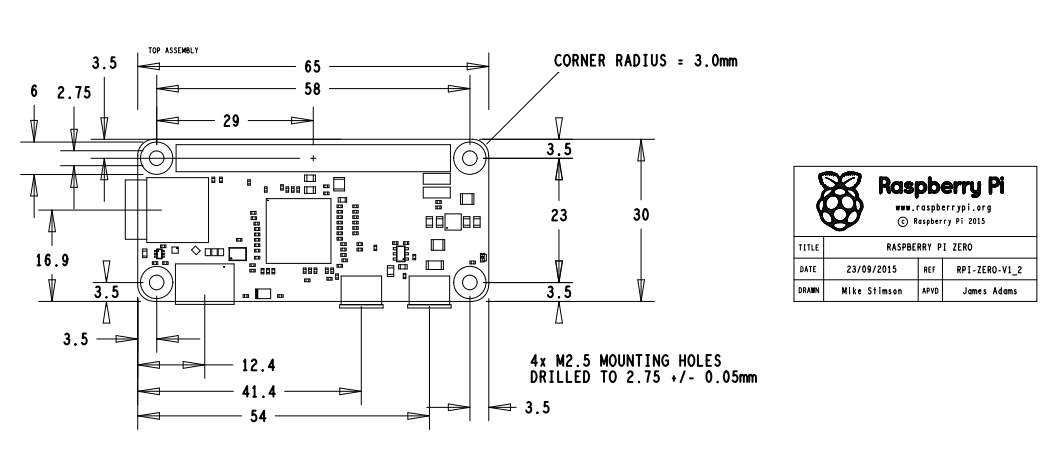
Pi Zero 1.2版机构图

Pi Zero虽然很便宜，但很多原先树莓派所具备的基本东西，其实是隐藏的，必须自己手工焊接才能取得功能，例如GPIO接脚。而有的功能根本就取消了，例如DSI连接器，这使得Pi Zero无缘连接触控面板。

因为大大便宜，所以隐藏或取消，大家通常会妥协接受，毕竟一片才5美元，总不能一切向20～35美元的树莓派看齐。

1.3版Pi Zero可接摄影机，价格不变

而到了2016年5月，也就是Pi Zero正式发售半年后，树莓派基金会对Pi Zero进行改版，推出1.3版，新版最大特点在于：除一切与1.2版相同外，原本20～35美元树莓派才具备的摄影机接口CSI连接器，也设置在1.3版上，使Pi Zero有机会连接摄影机。

Pi Zero 1.3版又可以接摄影机了。

确实，许多树莓派使用者会加装树莓派摄影机进行各种应用，原本的1.2版Pi Zero不能接摄影机实为一大憾事，而1.3版选择恢复。

但是1.3版Pi Zero依然不具备DSI界面，依据一般印象，树莓派用户使用CSI界面的机会多过DSI界面，或许基于这个原因，1.3版Pi Zero优先恢复CSI界面，但依然缺乏DSI界面。

恢复CSI接口的1.3版Pi Zero依然是以5美元发售，很明显的这一作法，会快速排挤掉原有1.2版的销售，在相同价位下，人人都想买有机会连接摄影机的1.3版Pi Zero。

Pi Zero W支持Wi-Fi及BLE，10美元可买到

到了2017年2月，树莓派基金会再推出Pi Zero W。Pi Zero W整个设计与1.3版Pi Zero相仿，但再加入Wi-Fi与蓝牙（Bluetooth）功能，Wi-Fi方面支持到IEEE 802.11n，蓝牙则支持到4.x版并含BLE（Bluetooth Low Energy）。

Pi Zero W支持Wi-Fi和BLE，价格为10美元。

Pi Zero W一样没把DSI连接器恢复，只具备CSI连接器，价位方面也稍提高了，成10美元，毕竟追加了无线通信芯片。Pi Zero W用的是与RPi 3 Model B相同的无线通信芯片，即

Cypress公司的CYW43438。看来，树莓派基金会有心让无线通信能力，逐渐变成未来树莓派计算机的基本配备。

最后有意思的是，Pi Zero W才一推出就有官方版的机壳（case）可用，有3种上盖可换替，且Pi Zero系列有新的配销商支持，在英国有ModMyPi，德国有pi3g，土耳其有Samm Teknoloji，法国、西班牙、意大利、葡萄牙则有Kubii，荷比卢（荷兰、比利时、卢森堡）则有Kiwi Electronics，这些业者都有卖Pi Zero，看来很快也会来美洲、亚洲吧！

官方版本的3款Pi Zero W外壳

原文参考

https://mp.weixin.qq.com/s?__biz=MzU0MTg0ODIzNA==&mid=2247484649&idx=3&sn=3a80babb5df63f6e518830e5919e8aed&chksm=fb22e32ccc556a3a954ef7fd8d8a4ab593f3fab3b46fcf8ff3b7c5d5f78353b34492de5568a5#rd