P3195 [HNOI2008]玩具装箱TOY

列出DP方程式:设f[i]表示分组完前i件物品的最小花费,为方便计算，
设sum[i]表示是前i件物品的长度和。
f[i]=min(f[j]+(sum[i]-sum[j]+i-j-L-1)^2) [0<=j<i]
求复杂度O(n)的解法

斜率优化入门题
对于这类方程f(i)=a(i)*b(j)+a(i)+b(j)
工具：构造直线，单调队列
令a(i)=sum(i)+i, b(j)=sum(j)+j+L+1
f(i)=f(j)+(a(i)-b(j))^2
=f(j)+a(i)^2-2*a(i)*b(j)+b(j)^2
2*a(i)*b(j)+f(i)-a(i)^2=f(j)+b(j)^2
//以j为变量，i为常量来看
坐标角度来讲，f(i)含义为：斜率为k=2*a(i)的直线过点P(b(j),f(j)+b(j)^2)与y轴的截距加上a(i)^2
即求这个截距的最小值
结合图像

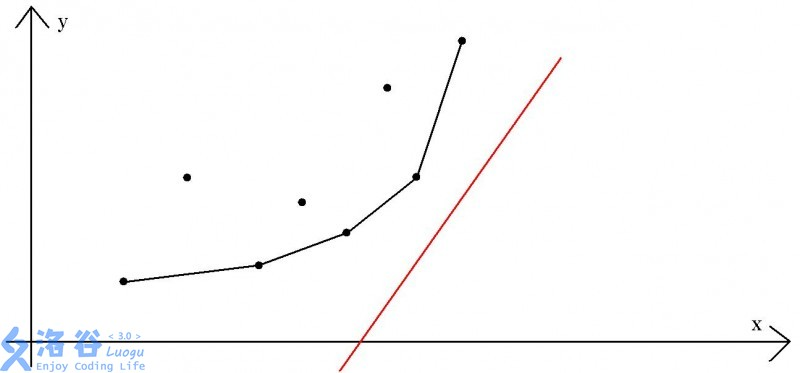
存在单调队列的最优的 P 点（图中用直线连接）组成了一个下凸包
几点说明：
1.随着i增加，目标斜率k=2*a(i)也在增加（sum(i)是前缀和）
2.目标坐标点为直线与凸包刚好相切的点，即slope(Pj,Pj+1)下面的斜率都小于k,上面斜率都大于k
单调队列：
对队首：while(slope(Phead,Phead+1)<2*a(i))head++; //把前面不要的都剪掉
筛选出来的q(head)即为最优解
f(i)=f(q(head))+(a(i)-b(q(head))^2
对队尾：while(slope(Ptail-1,Ptail)<slope(Ptail-1,Pi))tail--;q(++tail)=i;//如果新加入的Pi与Ptail-1的斜率更小，那么就替换掉Ptail

上代码：
inline db a(int i){return sum(i)+i;}
inline db b(int i){return a(i)+L+1;}
inline db X(int i){return b(i);}
inline db Y(int i){return f(i)+b(i)*b(i);}
inline db slope(int i,j){return (Y(i)-Y(j))/(X(i)-X(j));}

head=tail=1;
For(i,1,n){
while(head<tail&&slope(q(head),q(head+1))<2*a(i))head++;
f(i)=f(q(head))+(a(i)-b(q(head))*(a(i)-b(q(head));
whiel(slope(q(tail-1),q(tail))>slope(q(tail-1),i))tail--;
q(++tail)=i;
}
cout<<f(n);