利用gcc自带的功能-fstack-protector检测栈溢出及其实现【转】

转自：https://www.cnblogs.com/leo0000/p/5719186.html

最近又遇到了一个崩溃，栈回溯非常怪异。

/lib/i386-linux-gnu/libc.so.6(gsignal+0x4f) [0xb2b751df]
/lib/i386-linux-gnu/libc.so.6(abort+0x175) [0xb2b78825]
/lib/i386-linux-gnu/libc.so.6(+0x6b39a) [0xb2bb239a]
/lib/i386-linux-gnu/libc.so.6(__fortify_fail+0x45) [0xb2c4b0e5]
/lib/i386-linux-gnu/libc.so.6(+0x102eba) [0xb2c49eba]
/ramdisk/xxxxxx() [0x8467639]
/ramdisk/xxxxxx() [0x849a802]
/ramdisk/xxxxxx() [0x84b75da]
/ramdisk/xxxxxx(xxxxxxxxxxxx+0x444) [0x84b9224]

　　其中的xxxxx是公司的模块和函数，故隐藏，对接下去的分析没有影响。

　　一开始，因为没有接触过__fortify_fail这个函数，另外加上因为有一部分栈回溯没有对应的符号，我以为是数组溢出把栈信息破坏了。但实际上想想不对，如果是栈信息被破坏了，不出意外的话，应该是回溯不到某些很有序的函数的，这些函数我没上。

　　后来同事无意的一句话，说__fortify_fail是内存检测，我才百度了一下这个__fortify_fail函数，那么这个函数是什么情况下会被调用的呢？

一。gcc编译选项-fstack-protector和-fstack-protector-all

　　正是我在前面猜测的错误原因，牛人Stack Guard 就想出了保护栈信息的方式，在ebp和ip等信息的地址下面放一个保护数，如果栈溢出，那么这个8位数会被修改，就会导致函数进入栈溢出错误处理函数，也就是导致了上面的栈。

二。比较加选项前后的反汇编代码

　　源码：

#include <stdio.h>
int main()
{
        char a;
        int i;
        memcpy(&a,"ss",2);
        printf("1\n");
        memcpy(&i,"sssss",4);
        printf("2\n");
　　　　 return 0;
}

　　使用gdb调试该程序，首先查看a和i的地址，

(gdb) p &a
$1 = 0xbffff69b "\b\364\037\374\267\220\204\004\b"
(gdb) p &i
$2 = (int *) 0xbffff694

　　显然变量a的地址要高，更接近栈顶。可以证明i的溢出并不一定能被检测到，而a的检测一定会被检测到。

　　看下汇编代码的对比。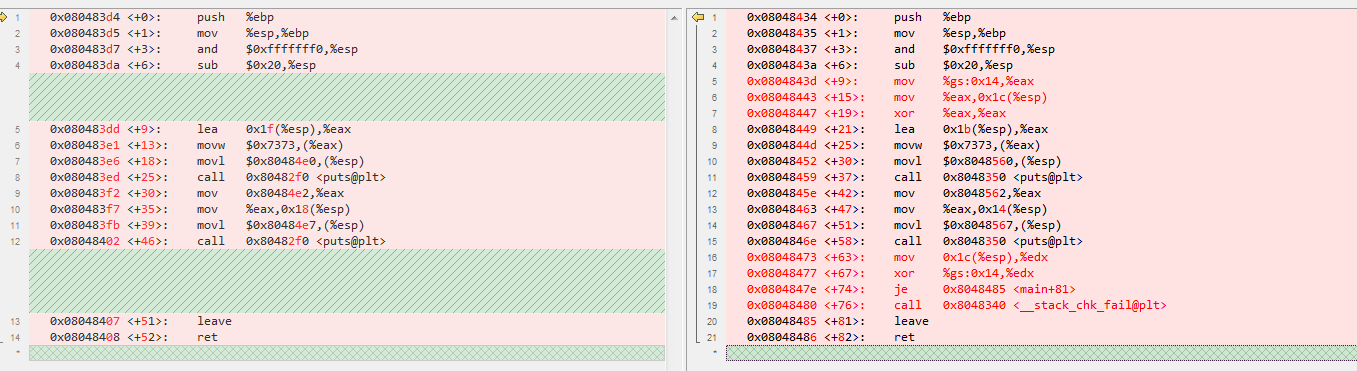

　　movw $0x7373那句话就是往a里面拷贝ss，所以整个程序前后的差异在于插入两段代码，这两段的代码就是用来检测局部变量。

　　运行溢出时的栈

#0  0xb7fdd424 in __kernel_vsyscall ()
#1  0xb7e4f1ef in raise () from /lib/i386-linux-gnu/libc.so.6
#2  0xb7e52835 in abort () from /lib/i386-linux-gnu/libc.so.6
#3  0xb7e8a2fa in ?? () from /lib/i386-linux-gnu/libc.so.6
#4  0xb7f20dd5 in __fortify_fail () from /lib/i386-linux-gnu/libc.so.6
#5  0xb7f20d8a in __stack_chk_fail () from /lib/i386-linux-gnu/libc.so.6
#6  0x08048485 in main ()

　　与本文最前面的错误是一致的

三。走读代码修改错误。

四。总结

　　当然这个举措并不能够完全的抑制栈溢出，如果跳过了保护数，那么还是检测不到栈溢出的，并且对其他的局部变量溢出没有保护。当然每个变量都保护会大大增加程序复杂度。