bzoj刷水

因为最近的生活太颓废总是不做题而被老师D了一番， 所以今天晚上到bzoj上去刷了几道水题。。。。。

 

bzoj 4320: ShangHai2006 Homework

题目大意

维护一个支持两个操作的集合：

1） 插入一个数x

2） 询问集合中所有数中 mod x 最小是多少

解题思路

似乎log家族没有什么好的办法解决这道题？

考虑 sqrt() 的方法。

当询问 x <= sqrt(m) 的时候， 直接存一下就可以了。

当询问 x > sqrt(m) 的时候，把n分成 n / x 块， 每一块单独考虑。

这时对于每一块， 我们需要求出的就是 >= (i * x) 的所有数中最小的那个。

填一个log会爆掉的。但是如果倒着处理， 每一次询问的就是 x 右面第一个没有被染色的点， 其实就是 疯狂的馒头这道题， 用并查集搞一搞就可以了。

,sq=;
     memset(tmp,     memset(ans,     ;i<=n;i++){
         ]; scanf(,&xx[i]);
         la[i]=s[]-                      bin[xx[i]]++;
             ;j<=sq;j++)tmp[j]=min(tmp[j],xx[i]%j);
         }     }
     ;i<=N;i++);
     fat[N+]=N+;
     ;i--){
                      ;
         }             ;j<=N;j+=xx[i])
                          }
     }
     ;i<=n;i++)     ;
 }

bzoj 4318:OSU!

题目大意

问一个长度为n， 第i为有pi的概率为1的01串期望的价值是多少。

一个01串的价值定义为它的所有极长子只含1串的长度的立方的和。

解题思路

尝试计算每一位对答案的贡献f(i)。 设li 为 i 前面的极长"1"串的长度

显然 f(i) = p[i] * (3 * li² + 3 * li + 1)。

只要算出 li² 和 li 的期望， 就可以算出 f(i) 的期望了。

注意 li² 的期望并不等于 （li的期望）² ， 要单独存一个数来转移。

虽然恶意缩了缩空格，，但代码真的本来就很短很漂亮。。

#include <cstdio>
;i<=n;i++){
        scanf(*x2+*xx+);
        x2=x*(x2+*xx+);
        xx=x*(xx+);
    }
    printf(;
}

bzoj 4302: Hdu 5301 Buildings

题目大意

有n*m的一个矩形地面，要建公寓，现在要求公寓里的房间怎么划分，要求每间房屋都为一个矩形，而且要有一侧为矩形的边，除(x,y)位置外不能有空余，(x,y)位置不能建房间，要让房屋面积最大的那个的面积尽量的小，问最小会是多少 

（上面这段是copy下来的。。）

解题思路

构造题。首先旋转一下令 n <= m，显然， 最后答案中覆盖的块一定都是 1 * x 的

其实整个问题的答案就是覆盖了障碍点的 上， 下， 左， 右 四个点的四个块的长度。

这时候情况数就很少了， 分类讨论一下就好了。

1）（障碍物）上面的点向上， 下面的点向下， 这时候剩下的点分两种情况： 1， 全部按照 (n + 1) / 2的方式竖着排列 2, 所有左边的点向左连， 右边的点向右连（其实第2种情况更优当且仅当是一个边长为奇数的正方形且障碍点在中间）

2）（障碍物）上面的点和下面的点都向 左边和右边中更近的那一边连 ， 这时候剩下的点（就是障碍物左边的所有点或者是右边的所有点）分两种情况： 1， 全部按照 (n + 1) / 2的方式竖着排列 2, 所有点都向左边/ 右边连。

好了， 其实一共只有四小类。

代码还是炒鸡短。。。

#include <iostream>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <cstdio>
) / , max(y - , m - y - )), max(x - , n - x));
        ans = min(ans, max(min(y, m - y + ), min((n + ) / , max(y - , m - y))));
        printf(;
}

bzoj 4305: 数列的GCD

题目大意

给出一个长度为N的数列{a[n]}，1<=a[i]<=M(1<=i<=N)。 

现在问题是，对于1到M的每个整数d，有多少个不同的数列b[1], b[2], ..., b[N]，满足： 

(1)1<=b[i]<=M(1<=i<=N)； 

(2)gcd(b[1], b[2], ..., b[N])=d； 

(3)恰好有K个位置i使得a[i]<>b[i](1<=i<=N)

1.  1≤bi≤m
2.  gcd(b1,b2,...,bn)=d
3.  ∑ni=1[ai≠bi]=k

解题思路

因为 300000 以内的数的因子个数最多也就140个， 所以这道题怎么搞一搞都可以。

然后就是一些基本数论知识也没什么好说的。对于每一个i ，只要求出a[]中有多少个数是i的倍数。对于不是i的倍数的那些数， 贡献的方案数是 数量^(n/i) , 对于是i的倍数的那些数， 贡献的是 从那么多数中选取(n-k)个数， 选出来的数每个有1种取法，其它的每个有(n/i)-1种取法。

代码有点丑就不贴了（竟然比绝大多数代码都长简直不能忍！！！一定是我的算法太丑了QAQ）

bzoj 3884: 上帝与集合的正确用法

题目大意

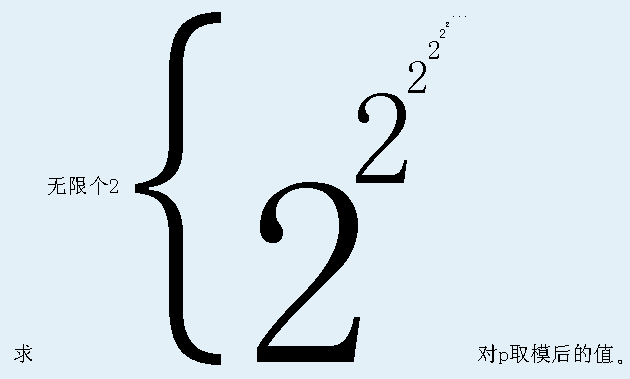
1.  1≤bi≤m
2.  gcd(b1,b2,...,bn)=d
3.  ∑ni=1[ai≠bi]=k

解题思路

我们都知道欧拉定理： aⁿ ≡ a^{n mod φ(p)}  mod p （gcd(a, p) = 1）

然而它竟然还有一个拓展：

aⁿ ≡ a^{n mod φ(p) +φ(p)}   mod p  这个公式是始终通用的

然后这道题就可以随便做了。设答案为 f(x)

则 f(x) = 2^{f(phi(x)) + phi(x)} mod x

于是就可以递归地解决啦

], prim[N], pp, f[N+], X[], mx;
 ];
      ;
              ) ret = (ll)ret * x % mod;
         x = (ll)x * x % mod; k >>= ;
     } }
      ) f[x] = mypow(, calc(phi[x]) + phi[x], x);
      }
      scanf(     ; i <= t; i ++) scanf(     ; i <= mx; i ++){
         ;
         ; j <= pp && (ll)i * prim[j] <= mx; j ++){
             isp[i * prim[j]] = ; phi[i * prim[j]] = phi[i] * (prim[j] - );
             ) {phi[i * prim[j]] = phi[i] * prim[j];          }
     }
     memset(f, -, (mx + ) * );
     f[] = ;
     ; i <= t; i ++) printf(    ;
 }