二项分布&超几何分布
伯努利分布 在一次试验中,事件A出现的概率为p,不出现的概率为q=1-p。若以β记事件A出现的次数,则β仅取0,1两值,相应的概率分布为:
二项分布是指在只有两个结果的n次独立的伯努利试验中,所期望的结果出现次数的概率。

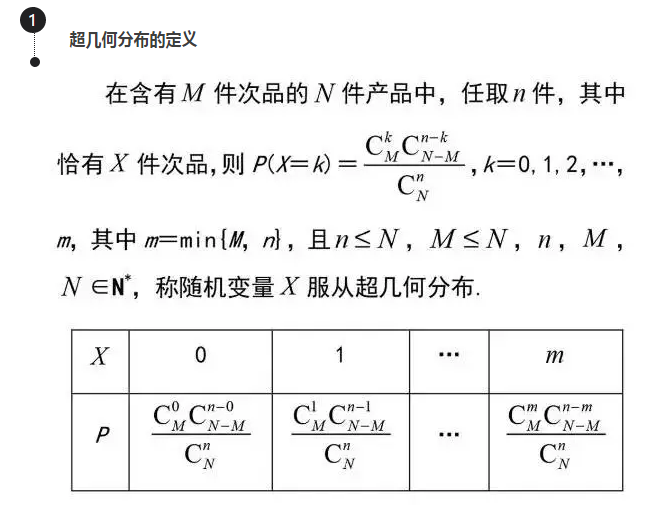




二项分布&超几何分布的更多相关文章
- 各类分布----二项分布,泊松分布,负二项分布,gamma 分布,高斯分布,学生分布,Z分布
伯努利实验: 如果无穷随机变量序列 是独立同分布(i.i.d.)的,而且每个随机变量 都服从参数为p的伯努利分布,那么随机变量 就形成参数为p的一系列伯努利试验.同样,如果n个随机变量 独立同 ...
- 二项分布和Beta分布
原文为: 二项分布和Beta分布 二项分布和Beta分布 In [15]: %pylab inline import pylab as pl import numpy as np from scipy ...
- 关于Beta分布、二项分布与Dirichlet分布、多项分布的关系
在机器学习领域中,概率模型是一个常用的利器.用它来对问题进行建模,有几点好处:1)当给定参数分布的假设空间后,可以通过很严格的数学推导,得到模型的似然分布,这样模型可以有很好的概率解释:2)可以利用现 ...
- 二项分布 多项分布 伽马函数 Beta分布
http://blog.csdn.net/shuimu12345678/article/details/30773929 0-1分布: 在一次试验中,要么为0要么为1的分布,叫0-1分布. 二项分布: ...
- 用Python学分析 - 二项分布
二项分布(Binomial Distribution)对Bernoulli试验序列的n次序列,结局A出现的次数x的概率分布服从二项分布- 两分类变量并非一定会服从二项分布- 模拟伯努利试验中n次独立的 ...
- 伯努利分布、二项分布、Beta分布、多项分布和Dirichlet分布与他们之间的关系,以及在LDA中的应用
在看LDA的时候,遇到的数学公式分布有些多,因此在这里总结一下思路. 一.伯努利试验.伯努利过程与伯努利分布 先说一下什么是伯努利试验: 维基百科伯努利试验中: 伯努利试验(Bernoulli tri ...
- 概率论中常见分布总结以及python的scipy库使用:两点分布、二项分布、几何分布、泊松分布、均匀分布、指数分布、正态分布
概率分布有两种类型:离散(discrete)概率分布和连续(continuous)概率分布. 离散概率分布也称为概率质量函数(probability mass function).离散概率分布的例子有 ...
- zoj3696Alien's Organ (二项分布,泊松分布求近似值)
/*二项分布即重复n次的伯努利试验,每次发生的概率一样,假设成功的概率是p,那么失败的概率就是1-p: 二项分布的概率公式:试验中发生K次的概率是 P(ξ=K)= C(n,k) * p^k * (1- ...
- Numpy随机数(一):超几何分布
超几何分布 产品抽样检查中经常遇到一类实际问题,假定在N件产品中有M件不合格品,即不合格率 . 在产品中随机抽n件做检查,发现k件不合格品的概率为 ,k=0,1,2,...,min{n,M}. Num ...
随机推荐
- Appium ios新的定位方式FindsByIosNSPredicate (没有试 先记录在这里) 有个 driver.find_element_by_ios_uiautomation() 研究下 ios的定位
这个定位方式需要用java-client -5.0.版本,4.x的版本没有这个定位方式 //输入账号和密码 driver.findElementByIosNsPredicate("value ...
- java代码--------实现随机输出100个随机数,10行,0--到9的数字
总结:妹纸不是那么会表述,如有不妥之处,请提出来 package com.sads; //杰伦的世界 //实现在0-100个数中,随机输出数每行10个数,也就是10行10列,这些数在0---到9之间 ...
- 老师金角大王的BLOG
首页: http://www.cnblogs.com/alex3714/ python3专题: http://www.cnblogs.com/alex3714/category/770733.html
- 第三章 Istio基本介绍
3.1 Istio的核心组件及其功能 Istio总体分两部分:控制面和数据面. 数据面(sidecar):sidecar通过注入的方式和业务容器共存于一个pod,会劫持业务容器的流量,并接受控制面组件 ...
- JavaScript笔记——使用AJax
在使用过JQuery之后,再来看JavaScript的Ajax实现就会觉得很麻烦,不过,最近使用到了,就记录一下吧 在JavaScript中Ajax的实现可以分为四步: 第一步 得到XMLHttpRe ...
- 5月9日上课笔记-网页定位、网页动画【HTML5】
一.网页定位 position: static (默认值) relative 相对定位(相对原来的位置) right left botton top absolute 绝对定位 fixed: 固定定位 ...
- [Cpp primer] Library string Type
In order to use string type, we need to include the following code #include<string> using std: ...
- canvas绘制路径
canvas绘制路径 方法 beginPath() 创建一个新的路径 lineTo() 描绘路径 closePath() 沿着路径画直线,并且画点移动到路径开头 stroke() 绘制形状 fill( ...
- Python实践练习:strip()的正则表达式版本
题目: 写一个函数,它接受一个字符串,做的事情和 strip()字符串方法一样.如果只传入了要去除的字符串,没有其他参数,那么就从该字符串首尾去除空白字符.否则,函数第二个参数指定的字符将从该字符串中 ...
- Python实践练习:在 Wiki 标记中添加无序列表
题目描述 项目:在 Wiki 标记中添加无序列表 在编辑一篇维基百科的文章时,你可以创建一个无序列表,即让每个列表项占据一行,并在前面放置一个星号.但是假设你有一个非常大的列表,希望添加前面的星号.你 ...
