MACD 的数学解释

目录

• MACD 的数学解释
  • MACD 的一般定义
  • 引入延迟算子
  • Taylor 展开
  • 权重分析
  • 共振？

MACD 的数学解释

MACD 的一般定义

\[\begin{align*}
DIF &= EMA(P, w_{fast}) - EMA(P,w_{slow}) \\
DEM &= EMA(DIF, w_{signal}) \\
BAR &= 2 \times (DIF - DEM)
\end{align*}
\]

引入延迟算子

将 \(w\) 定义为 \(EMA\) 的衰减系数，即

\[EMA_t = (1-w) \cdot P_t + w \cdot EMA_{t-1}
\]

将 \(L\) 定义为“延迟算子”，公式重写成：

\[EMA_t = \frac{1-w}{1-wL} P_t
\]

进而推导出：

\[\begin{align*}
DIF_t &= \left( \frac{1-w_{fast}}{1-w_{fast}L} - \frac{1-w_{slow}}{1-w_{slow}L} \right) P_t \\
DEM_t &= \frac{1-w_{signal}}{1-w_{signal}L} P_t \\
BAR_t &= 2\cdot DIF_t \frac{w_{signal}(1-L)}{1-w_{signal}L} \\
&= 2 \cdot \frac{w_{signal}(1-L)}{1-w_{signal}L} \cdot \frac{(w_{slow} - w_{fast})(1-L)}{(1-w_{slow}L)(1-w_{fast}L)} P_t
\end{align*}
\]

下面解析 \(BAR_t\) 的计算中，历史数据的权重。

Taylor 展开

采用最通常的参数配置 \(MACD(12,26,9)\)，即

\[\begin{align*}
w_{fast} &= (12-1) / (12+1) = 11/13 \\
w_{slow} &= (26-1) / (26+1) = 25/27 \\
w_{signal} &= (9-1) / (9+1) = 8/10 = 4/5
\end{align*}
\]

要得到历史数据在公式中的权重，必须对分数形式算子做 Taylor 展开，得到多项式级数的表达形式。将上述参数代入到公式中：

\[BAR_t =2 \cdot \frac{4/5(1-L)}{1-4/5L} \cdot \frac{(25/27 - 11/13)(1-L)}{(1-25/27L)(1-11/13L)} P_t
\]

在网站 WolframAlpha 上找到 Taylor 展开，输入上述公式

taylor series 2*(4/5*(1-x))/(1-4/5*x) * ((25/27 - 11/13)*(1-x))/((1-25/27*x)*(1-11/13*x))

得到 Taylor 展开的解析形式：

\[f(L) = \sum_{n=0}^{\infty}
\frac{32\left(819(\frac{4}{5})^n - 765(\frac{11}{13})^n + 65(\frac{25}{27})^n \right)}{29835} L^n
\]

所以，历史数据 \(P_{t-n}\) 的权重是：

\[\frac{32\left(819(\frac{4}{5})^n - 765(\frac{11}{13})^n + 65(\frac{25}{27})^n \right)}{29835}
\]

权重分析

画出前 50 个历史数据的权重

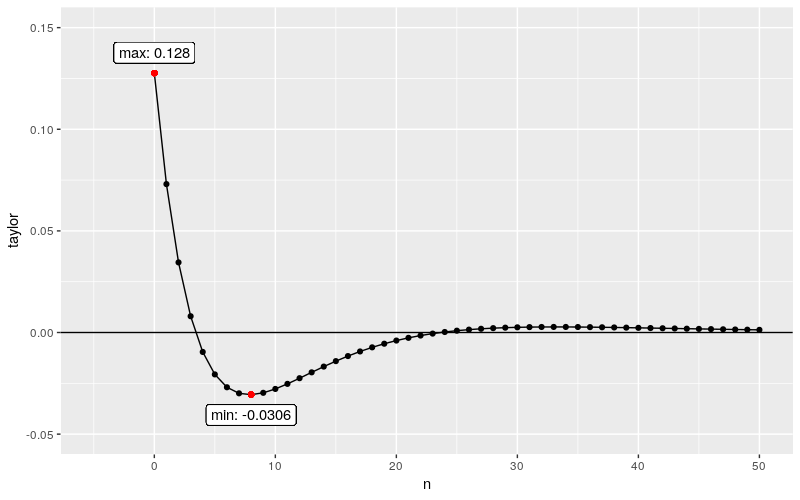
整体来看，权重的分布为三段：

1. 近期的数据赋予正的权重，但迅速衰减
2. 中期的数据赋予负的权重，绝对值先增后减
3. 远期的数据权重几乎为 0

\(MACD\) 中的 \(BAR\) 基本上可以看作是近期数据与中期数据的差。

共振？

如图，采用最通常的参数配置 \(MACD(12,26,9)\)，最大权重出现在 \(n=0\) 时，最小权重出现在 \(n=8\) 时。如果价格序列体现出“波浪”的形态，一个波谷到邻近波峰之间索引的差值等于 \(8-0\)，按照上述权重的分布，基本上可以断定这时的 \(BAR\) 同时达到了最大值，因为我们为波分和波谷分别赋予了最大和最小的权重。也就是说，价格序列波浪的长度大致等于最大最小权重对应索引的差时，价格序列和 \(BAR\) 将出现“共振”。