hdu 3507 斜率优化

我的第一道斜率优化。

就这道题而言，写出原始的方程：

　　dp[i] = min{ dp[j] + (sum[i]-sum[j])²  + M | j in [0,i) }

O(n^2)的复杂度肯定超时，要么优化转移，要么重写方程。

斜率优化的思想就是减少不必要的枚举（即不枚举肯定不会成为决策点的j）。

我们考虑两个位置p<q<i

“选择q比选择p优” 当且仅当 dp[q]+(sum[i]-sum[q])²+M < dp[p]+(sum[i]-sum[p])²+M

化简右边即：

[ (dp[q]+sum²[q])-(dp[p]+sum²[p]) ] / ( sum[q]-sum[p] ) < sum[i]*2

该式可以看成两个点连线的斜率：( sum[q], dp[q]+sum²[q] ) 与 ( sum[p], dp[p]+sum²[p] ) 两点。

文字语言就是：“将每个决策位置看成一个二维坐标系下的点，对于两个决策点，后者比前者优 当且仅当 两点连线的斜率小于sum[i]*2”

这样怎么减少不必要的枚举呢？

可以发现，所有决策点一定是单调不下降的（题中可能出现权值为0，此时有可能出现斜率为正无穷，若M=0，还有可能出现重点，所以计算斜率不要用除法）

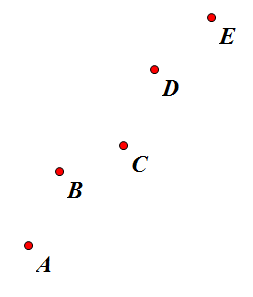
上面的B点一定是不会成为最优决策点的，反证法：

如果B成为最优决策点，那么

2*sum[i]>k_ab 且 2*sum[i]<k_bc

而显然k_ab > k_bc ，这样就推出了2*sum[i]>k_ab >k_bc >2*sum[i]，矛盾。

故B不可能成为最优决策点，同理，D也不行，删掉这些点后，我们剩下的图形就是一个下凸的图形了：

我们维护这样一个下凸的图形到队列中：

当要查找i位置的最优决策点时，一直删除队首的点，直到队中的第一条直线的斜率大于2*sum[i]或队中只有一个点，此时队首元素就是最优决策点。

计算完i位置后，要将i位置对应的点加入到队列中，此时会删除一些对尾的点，以保持队中点的下凸性（注意处理重合的点）。

这样，我们就利用斜率优化掉了很多不必要的枚举，将时间复杂度从O(n^2)降到了O(n)。

 #include <cstdio>
 #define ln(A,B) ((B)-(A))
 #define maxn 500010

 typedef long long lng;

 struct Vector {
     lng x, y;
     int id;
     Vector(){}
     Vector( lng x, lng y, int id ) : x(x), y(y), id(id) {}
     Vector operator-( const Vector & b ) const { return Vector(x-b.x,y-b.y,); }
     lng operator&( const Vector & b ) const {
         return x*b.y-y*b.x;
     }
 };
 typedef Vector Point;

 int n, m;
 int cost[maxn];
 lng sum[maxn];
 lng dp[maxn];

 int beg, end;
 Point qu[maxn];

 int main() {
     while(  ) {
         if( scanf( "%d%d", &n, &m )!= ) return ;

         sum[] = ;
         for( int i=; i<=n; i++ ) {
             scanf( "%d", cost+i );
             sum[i] = sum[i-]+cost[i];
         }

         dp[] = ;
         qu[beg=end=] = Point( , ,  );

         for( int i=; i<=n; i++ ) {
             while( end>beg && qu[beg+].y-qu[beg].y<=(qu[beg+].x-qu[beg].x)**sum[i] )
                 beg++;
             int j = qu[beg].id;
             dp[i] = dp[j]+(sum[i]-sum[j])*(sum[i]-sum[j])+m;
             Point npt = Point( sum[i], dp[i]+sum[i]*sum[i], i );
             while( end>beg && (ln(qu[end-],qu[end])&ln(qu[end-],npt))<= )
                 end--;
             qu[++end] = npt;
         }
         printf( "%lld\n", dp[n] );
     }
 }