【bzoj1951】: [Sdoi2010]古代猪文 数论-中国剩余定理-Lucas定理

【bzoj1951】: [Sdoi2010]古代猪文

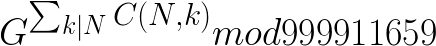
因为999911659是个素数

欧拉定理得

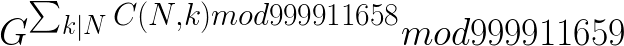
然后指数上中国剩余定理

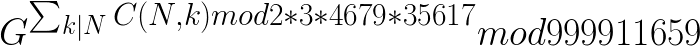
然后分别lucas定理就好了

注意G==P的时候的特判

 /* http://www.cnblogs.com/karl07/ */
 #include <cstdlib>
 #include <cstdio>
 #include <cstring>
 #include <cmath>
 #include <algorithm>
 using namespace std;
 #define ll long long

 const ll P=;
 const ll p1[] = {, , , , };
 const ll N=;
 ll g,n,cnt=;
 ll fac[N+],ifac[N+];
 ll p[N],ans[];

 ll Q_pow(ll a,ll b,ll p){
     ll ans=;
     while (b){
         if (b&) ans=ans*a%p;
         a=a*a%p;
         b=(b>>);
     }
     return ans;
 }

 void FAC(ll p){
     ifac[]=fac[]=;
     for (int i=;i<=N;i++) fac[i]=fac[i-]*i%p,ifac[i]=Q_pow(fac[i],p-,p);
 }

 ll C(ll n,ll m,ll p){
     if (m>n) return ;
     return fac[n]*ifac[m]%p*ifac[n-m]%p;
 }

 ll lucas(ll n,ll m,ll p){
     if (m==) return ;
     return lucas(n/p,m/p,p)*C(n%p,m%p,p)%p;
 }

 void fj(ll x){
     for (int i=;i*i<=x;i++){
         if (x%i==){
             p[++cnt]=i;
             if (i*i!=x) p[++cnt]=n/i;
         }
     }
 }

 ll gcd(ll a,ll b){return b ? gcd(b,a%b) : a;}

 void ex_gcd(ll a,ll b,ll &x,ll &y){
     if (b==){x=;y=;return;}
     ex_gcd(b,a%b,y,x);
     y-=x*(a/b);
 }

 ll China(){
     ll a0=ans[],p0=p1[];
     for (int i=;i<=;i++){
         ll x,y,g=gcd(p0,p1[i]);
         ex_gcd(p0,p1[i],x,y);
         x=(x*(ans[i]-a0)%p1[i]+p1[i])%p1[i];
         a0=a0+x*p0;
         p0=p0/g*p1[i];
     }
     return a0;
 }

 void work(){
     for(int i=;i<=;i++){
         FAC(p1[i]);
         for (int j=;j<=cnt;j++){
             ans[i]=(ans[i]+lucas(n,n/p[j],p1[i]))%p1[i];
         }
     }
     printf("%lld\n",Q_pow(g,China(),P));
 }

 int main(){
     scanf("%lld%lld",&n,&g);
     if (g==P) {puts(""); return ;}
     fj(n);
     work();
     return ;
 }
 　　

各种zz的错误。。调了一年

而且跑的巨慢无比。。