AVL树（自平衡二叉查找树）

了解AVL树之前要先了解二叉查找树（BST），BST查找元素的时间复杂度平均是O(logN)，最坏的情况是O(N)，所有的元素都接在左子树（或者右子树）就相当于一串链表了。而AVL树会对子树过高的情况进行优化，这里有个平衡因子的概念，当前节点的平衡因子=左子树高度-右子树高度，AVL树的每一个节点的平衡因子的绝对值都是 ＜ 2 的。

当一个新节点插入AVL树 ( 根节点为tree ) 的时候会有四种情况：

假设距离新节点最近的失衡节点为 t （ t 的平衡因子的绝对值达到了2，且距离新节点最近）

1、LL型：新节点在 t1 的左孩子的左子树上，需要对 t 进行一次右旋操作；

2、RR型：新节点在 t 的右孩子的右子树上，需要对 t 进行一次左旋操作；

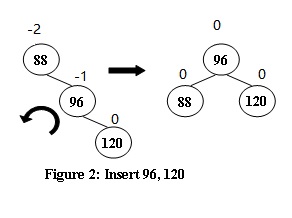
3、LR型：新节点在 t 的左孩子的右子树上，需要先对 t 的左孩子进行一次RR（左旋）操作，然后对 t 进行一次LL（右旋）操作；

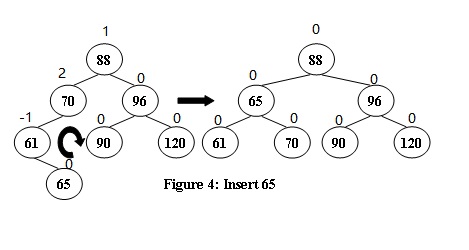
4、RL型：新节点在 t 的右孩子的左子树上，需要先对 t 的右孩子进行一次LL（右旋）操作，然后对 t 进行一次RR（左旋）操作；

AVL树的实现代码如下：

 #include "pch.h"
 #include <iostream>
 #include <queue>
 #define ElementType int//自定义元素类型
 using namespace std;
 typedef struct node *AVLTree;
 struct node {
     ElementType key;
     int Height = ;
     AVLTree left = NULL, right = NULL;
 };
 int Height(AVLTree tree);//求树的高度
 ElementType Max(ElementType a, ElementType b);
 AVLTree insert(AVLTree tree, ElementType &key);//在AVLTree中插入节点
 AVLTree LL_Rotation(AVLTree tree);//LL旋转
 AVLTree RR_Rotation(AVLTree tree);//RR旋转
 AVLTree LR_Rotation(AVLTree tree);//LR旋转
 AVLTree RL_Rotation(AVLTree tree);//RL旋转

 void levelTraversal(AVLTree tree);//层序遍历，用于测试

 /*用main函数来测试，给N个不同的数据，插入AVL树中，然后层序输出*/
 int main()
 {
     int N;
     ElementType key;
     AVLTree tree = NULL;
     scanf("%d", &N);
     for (int i = ; i < N; i++) {
         cin >> key;
         tree = insert(tree, key);
     }
     levelTraversal(tree);
 }

 AVLTree insert(AVLTree tree, ElementType &key) {
     if (tree == NULL) {
         tree = new node();
         tree->key = key;
     }
     else if (key < tree->key) {
         tree->left = insert(tree->left, key);//key小于当前节点的值时继续往其左子树递归地插入
         if (Height(tree->left) - Height(tree->right) >= ) {//左子树与右子树的高度差达到2的时候就要对当前节点进行旋转，这里由于是递归地执行，保证了平衡因子达到2的节点是最接近插入点的
             if (key < tree->left->key)
                 tree = LL_Rotation(tree);
             else
                 tree = LR_Rotation(tree);
         }
     }
     else {
         tree->right = insert(tree->right, key);
         if (Height(tree->right) - Height(tree->left) >= ) {
             if (key > tree->right->key)
                 tree = RR_Rotation(tree);
             else
                 tree = RL_Rotation(tree);
         }
     }
     tree->Height = Max(Height(tree->left), Height(tree->right)) + ;//当前节点的高度为其最大子树的高度+1
     return tree;
 }

 AVLTree LR_Rotation(AVLTree tree) {
     tree->left = RR_Rotation(tree->left);
     return LL_Rotation(tree);
 }

 AVLTree RL_Rotation(AVLTree tree) {
     tree->right = LL_Rotation(tree->right);
     return RR_Rotation(tree);
 }

 AVLTree RR_Rotation(AVLTree tree) {
     AVLTree tree2 = tree->right;
     tree->right = tree2->left;
     tree2->left = tree;
     tree->Height = Max(Height(tree->left), Height(tree->right)) + ;
     tree2->Height = Max(Height(tree2->right), tree->Height) + ;
     return tree2;
 }

 AVLTree LL_Rotation(AVLTree tree) {
     AVLTree tree2 = tree->left;
     tree->left = tree2->right;
     tree2->right = tree;
     tree->Height = Max(Height(tree->left), Height(tree->right)) + ;
     tree2->Height = Max(Height(tree->left), tree->Height) + ;
     return tree2;
 }

 int Height(AVLTree tree) {
     if (tree == NULL)
         return ;
     return tree->Height;
 }

 ElementType Max(ElementType a, ElementType b) {
     return a > b ? a : b;
 }

 void levelTraversal(AVLTree tree)
 {
     queue <AVLTree> Q;
     Q.push(tree);
     while (!Q.empty()) {
         AVLTree t = Q.front();
         Q.pop();
         cout << t->key << " ";
         if (t->left != NULL)
             Q.push(t->left);
         if (t->right != NULL)
             Q.push(t->right);
     }
 }