HDU-6395 多校7 Sequence（除法分块+矩阵快速幂）

Sequence

Time Limit: 4000/2000 MS (Java/Others)    Memory Limit: 262144/262144 K (Java/Others)
Total Submission(s): 1731    Accepted Submission(s): 656

Problem Description

Let us define a sequence as below

F1=A

F2=B

Fn=C⋅Fn−2+D⋅Fn−1+⌊Pn⌋

Your job is simple, for each task, you should output Fn module 109+7.

 

Input

The first line has only one integer T, indicates the number of tasks.

Then, for the next T lines, each line consists of 6 integers, A , B, C, D, P, n.

1≤T≤200≤A,B,C,D≤1091≤P,n≤109

 

Sample Input

2

3 3 2 1 3 5

3 2 2 2 1 4

 

Sample Output

36

24

 

Source

2018 Multi-University Training Contest 7

 

 

 

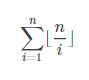
cin>>n;
ll ans = ;
for(ll l = ,r;l <= n;l = r + ){
     r = n / (n / l);
     ans += (r - l + ) * (n / l);
}
cout<<ans<<endl;

除法分块模板

 

[p/n]是整除，一段内的值是相同的，他的整除值有sqrt（p）种。

因此可以将变量分块每块看作常量，对每一块使用矩阵快速幂。

 

 

#include<iostream>
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<math.h>
#include<algorithm>
#define MAX 10
#define INF 0x3f3f3f3f
#define MOD 1000000007
using namespace std;
typedef long long ll;

ll p,q;
struct mat{
    ll a[MAX][MAX];
};

mat operator *(mat x,mat y)
{
    mat ans;
    memset(ans.a,,sizeof(ans.a));
    for(int i=;i<=;i++){
        for(int j=;j<=;j++){
            for(int k=;k<=;k++){
                ans.a[i][j]+=x.a[i][k]*y.a[k][j]%MOD;
                ans.a[i][j]%=MOD;
            }
        }
    }
    return ans;
}
mat qMod(ll x,mat a,ll n)
{
    mat t;
    t.a[][]=q;t.a[][]=p;t.a[][]=x;
    t.a[][]=;t.a[][]=;t.a[][]=;
    t.a[][]=;t.a[][]=;t.a[][]=;
    while(n){
        if(n&) a=t*a;
        n>>=;
        t=t*t;
    }
    return a;
}
int main()
{
    int t,i;
    ll a1,a2,x,n;
    scanf("%d",&t);
    while(t--){
        scanf("%lld%lld%lld%lld%lld%lld",&a1,&a2,&p,&q,&x,&n);
        if(n==) printf("%lld\n",a1);
        else if(n==) printf("%lld\n",a2);
        else{
            mat a;
            a.a[][]=a2;a.a[][]=;a.a[][]=;
            a.a[][]=a1;a.a[][]=;a.a[][]=;
            a.a[][]=;a.a[][]=;a.a[][]=;
            if(x>=n){
                for(i=;i<=n;i=x/(x/i)+){
                    a=qMod(x/i,a,min(n,x/(x/i))-i+);
                }
            }
            else{
                for(i=;i<=x;i=x/(x/i)+){
                    a=qMod(x/i,a,x/(x/i)-i+);
                }
                a=qMod(,a,n-max(x,2ll));
            }
            printf("%lld\n",a.a[][]);
        }
    }
    return ;
}