浮点数在计算机内存中的表示（IEEE 754规定1位是符号位，8位是指数，剩下的23位为有效数字）

本文转载自：阮一峰的博客，http://www.ruanyifeng.com/blog/2010/06/ieee_floating-point_representation.html

张玉彬的博客 http://www.cnblogs.com/jillzhang/archive/2007/06/24/793901.html

1.
前几天，我在读一本C语言教材，有一道例题：

　　#include <stdio.h>

　　void main(void){

　　　　int num=9; /* num是整型变量，设为9 */

　　　　float* pFloat=&num; /* pFloat表示num的内存地址，但是设为浮点数 */

　　　　printf("num的值为：%d\n",num); /* 显示num的整型值 */

　　　　printf("*pFloat的值为：%f\n",*pFloat); /* 显示num的浮点值 */

　　　　*pFloat=9.0; /* 将num的值改为浮点数 */

　　　　printf("num的值为：%d\n",num); /* 显示num的整型值 */

　　　　printf("*pFloat的值为：%f\n",*pFloat); /* 显示num的浮点值 */

　　}

运行结果如下：

　　num的值为：9
　　*pFloat的值为：0.000000
　　num的值为：1091567616
　　*pFloat的值为：9.000000

我很惊讶，num和*pFloat在内存中明明是同一个数，为什么浮点数和整数的解读结果会差别这么大？

要理解这个结果，一定要搞懂浮点数在计算机内部的表示方法。我读了一些资料，下面就是我的笔记。

2.
在讨论浮点数之前，先看一下整数在计算机内部是怎样表示的。

　　int num=9;

上面这条命令，声明了一个整数变量，类型为int，值为9（二进制写法为1001）。普通的32位计算机，用4个字节表示int变量，所以9就被保存为00000000 00000000 00000000 00001001，写成16进制就是0x00000009。

那么，我们的问题就简化成：为什么0x00000009还原成浮点数，就成了0.000000？

3.
根据国际标准IEEE 754，任意一个二进制浮点数V可以表示成下面的形式：

　　 $V = (-1)^s\times M\times 2^E$

　　（1）(-1)^s表示符号位，当s=0，V为正数；当s=1，V为负数。

　　（2）M表示有效数字，大于等于1，小于2。

　　（3）2^E表示指数位。

举例来说，十进制的5.0，写成二进制是101.0，相当于1.01×2^2。那么，按照上面V的格式，可以得出s=0，M=1.01，E=2。

十进制的-5.0，写成二进制是-101.0，相当于-1.01×2^2。那么，s=1，M=1.01，E=2。

IEEE 754规定，对于32位的浮点数，最高的1位是符号位s，接着的8位是指数E，剩下的23位为有效数字M。

对于64位的浮点数，最高的1位是符号位S，接着的11位是指数E，剩下的52位为有效数字M。

5.
IEEE 754对有效数字M和指数E，还有一些特别规定。

前面说过，1≤M<2，也就是说，M可以写成1.xxxxxx的形式，其中xxxxxx表示小数部分。IEEE 754规定，在计算机内部保存M时，默认这个数的第一位总是1，因此可以被舍去，只保存后面的xxxxxx部分。比如保存1.01的时候，只保存01，等到读取的时候，再把第一位的1加上去。这样做的目的，是节省1位有效数字。以32位浮点数为例，留给M只有23位，将第一位的1舍去以后，等于可以保存24位有效数字。

至于指数E，情况就比较复杂。

首先，E为一个无符号整数（unsigned int）。这意味着，如果E为8位，它的取值范围为0~255；如果E为11位，它的取值范围为0~2047。但是，我们知道，科学计数法中的E是可以出现负数的，所以IEEE 754规定，E的真实值必须再减去一个中间数，对于8位的E，这个中间数是127；对于11位的E，这个中间数是1023。

比如，2^10的E是10，所以保存成32位浮点数时，必须保存成10+127=137，即10001001。

然后，指数E还可以再分成三种情况：

（1）E不全为0或不全为1。这时，浮点数就采用上面的规则表示，即指数E的计算值减去127（或1023），得到真实值，再将有效数字M前加上第一位的1。

（2）E全为0。这时，浮点数的指数E等于1-127（或者1-1023），有效数字M不再加上第一位的1，而是还原为0.xxxxxx的小数。这样做是为了表示±0，以及接近于0的很小的数字。

（3）E全为1。这时，如果有效数字M全为0，表示±无穷大（正负取决于符号位s）；如果有效数字M不全为0，表示这个数不是一个数（NaN）。

好了，关于浮点数的表示规则，就说到这里。

下面，让我们回到一开始的问题：为什么0x00000009还原成浮点数，就成了0.000000？

首先，将0x00000009拆分，得到第一位符号位s=0，后面8位的指数E=00000000，最后23位的有效数字M=000 0000 0000 0000 0000 1001。

由于指数E全为0，所以符合上一节的第二种情况。因此，浮点数V就写成：

　　V=(-1)^0×0.00000000000000000001001×2^(-126)=1.001×2^(-146)

显然，V是一个很小的接近于0的正数，所以用十进制小数表示就是0.000000。

7.
再看例题的第二部分。

请问浮点数9.0，如何用二进制表示？还原成十进制又是多少？

首先，浮点数9.0等于二进制的1001.0，即1.001×2^3。

那么，第一位的符号位s=0，有效数字M等于001后面再加20个0，凑满23位，指数E等于3+127=130，即10000010。

所以，写成二进制形式，应该是s+E+M，即0 10000010 001 0000 0000 0000 0000 0000。这个32位的二进制数，还原成十进制，正是1091567616。

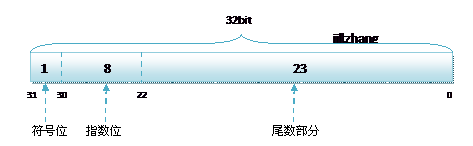
无论是单精度还是双精度在存储中都分为三个部分：

符号位(Sign) : 0代表正，1代表为负
指数位（Exponent）:用于存储科学计数法中的指数数据，并且采用移位存储
尾数部分（Mantissa）：尾数部分

其中float的存储方式如下图所示：

而双精度的存储方式为:

R32.24和R64.53的存储方式都是用科学计数法来存储数据的，比如8.25用十进制的科学计数法表示就为:8.25*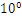,而120.5可以表示为:1.205*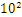,这些小学的知识就不用多说了吧。而我们傻蛋计算机根本不认识十进制的数据，他只认识0，1，所以在计算机存储中，首先要将上面的数更改为二进制的科学计数法表示，8.25用二进制表示可表示为1000.01,我靠，不会连这都不会转换吧?那我估计要没辙了。120.5用二进制表示为：1110110.1用二进制的科学计数法表示1000.01可以表示为1.0001*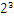,1110110.1可以表示为1.1101101*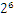,任何一个数都的科学计数法表示都为1.xxx*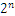,尾数部分就可以表示为xxxx,第一位都是1嘛，干嘛还要表示呀？可以将小数点前面的1省略，所以23bit的尾数部分，可以表示的精度却变成了24bit，道理就是在这里，那24bit能精确到小数点后几位呢，我们知道9的二进制表示为1001，所以4bit能精确十进制中的1位小数点，24bit就能使float能精确到小数点后6位，而对于指数部分，因为指数可正可负，8位的指数位能表示的指数范围就应该为:-127-128了，所以指数部分的存储采用移位存储，存储的数据为元数据+127，下面就看看8.25和120.5在内存中真正的存储方式。

首先看下8.25，用二进制的科学计数法表示为:1.0001*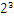

按照上面的存储方式，符号位为:0，表示为正，指数位为:3+127=130 ,位数部分为,故8.25的存储方式如下图所示:

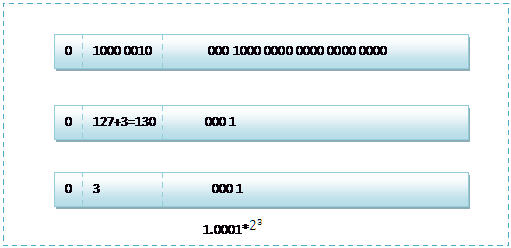
而单精度浮点数120.5的存储方式如下图所示:

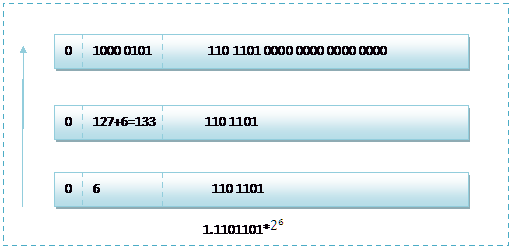
那么如果给出内存中一段数据，并且告诉你是单精度存储的话，你如何知道该数据的十进制数值呢？其实就是对上面的反推过程，比如给出如下内存数据：0100001011101101000000000000，首先我们现将该数据分段，0 10000 0101 110 1101 0000 0000 0000 0000，在内存中的存储就为下图所示：

根据我们的计算方式，可以计算出，这样一组数据表示为:1.1101101*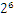=120.5

而双精度浮点数的存储和单精度的存储大同小异，不同的是指数部分和尾数部分的位数。所以这里不再详细的介绍双精度的存储方式了，只将120.5的最后存储方式图给出，大家可以仔细想想为何是这样子的

下面我就这个基础知识点来解决一个我们的一个疑惑，请看下面一段程序，注意观察输出结果

float f = 2.2f;
            double d = (double)f;
            Console.WriteLine(d.ToString("0.0000000000000"));
            f = 2.25f;
            d = (double)f;
            Console.WriteLine(d.ToString("0.0000000000000"));

可能输出的结果让大家疑惑不解，单精度的2.2转换为双精度后，精确到小数点后13位后变为了2.2000000476837，而单精度的2.25转换为双精度后，变为了2.2500000000000，为何2.2在转换后的数值更改了而2.25却没有更改呢？很奇怪吧？其实通过上面关于两种存储结果的介绍，我们已经大概能找到答案。首先我们看看2.25的单精度存储方式，很简单 0 1000 0001 001 0000 0000 0000 0000 0000,而2.25的双精度表示为:0 100 0000 0001 0010 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000,这样2.25在进行强制转换的时候，数值是不会变的，而我们再看看2.2呢，2.2用科学计数法表示应该为：将十进制的小数转换为二进制的小数的方法为将小数*2，取整数部分，所以0.282=0.4，所以二进制小数第一位为0.4的整数部分0，0.4×2=0.8，第二位为0,0.8*2=1.6,第三位为1，0.6×2 = 1.2，第四位为1，0.2*2=0.4，第五位为0，这样永远也不可能乘到=1.0，得到的二进制是一个无限循环的排列 00110011001100110011... ,对于单精度数据来说，尾数只能表示24bit的精度，所以2.2的float存储为:

但是这样存储方式，换算成十进制的值，却不会是2.2的，应为十进制在转换为二进制的时候可能会不准确，如2.2，而double类型的数据也存在同样的问题，所以在浮点数表示中会产生些许的误差，在单精度转换为双精度的时候，也会存在误差的问题，对于能够用二进制表示的十进制数据，如2.25，这个误差就会不存在，所以会出现上面比较奇怪的输出结果。

本文属作者原创，只发布在博客园，希望大家在转载的时候，注明出处和作者，谢谢。

http://blog.csdn.net/tenlee/article/details/49123593