[POI2007]石头花园SKA

Description

Blue Mary是一个有名的石头收藏家。迄今为止，他把他的藏品全部放在他的宫殿的地窖中。现在，他想将他的藏品陈列在他的花园中。皇家花园是一个边长为1000000000单位的平行于坐标轴的正方形。对于每个石头，Blue Mary都有一个他想放置的坐标，然后将他告诉他的属下。不幸的是，他忘了告诉他们坐标的顺序（比如无法分辨(x,y)和(y,x)）。属下们，就自己决定了每个石头的具体位置。为了保护他的藏品，Blue Mary决定建造一个篱笆来保护他们。为了美学的需要，篱笆也被设计为平行于坐标轴的矩形。如果花园的布局知道了，那么就可以知道最短长度的篱笆的布局。他的属下们需要变换石头的坐标使得篱笆的长度最少。每个石头只能从(x,y)变换为(y,x)，由于每个石头的重量不一样。属下们希望他们移动的石头的重量和最少。

Input

第一行包含一个数n，表示石头的数量

接下来n行分别描述n个石头的初始坐标和重量\(x_i,y_i,m_i\)。

(0<=\(x_i,y_i\)<=1000000000，1<=\(m_i\)<=2000)

(2<=n<=1000000)

Output

一行包含两个数由一个空格分割。

最小的篱笆长度和最小的移动的石子的重量和

Sample Input

5

2 3 400

1 4 100

2 2 655

3 4 100

5 3 277

Sample Output

10 200

HINT

---

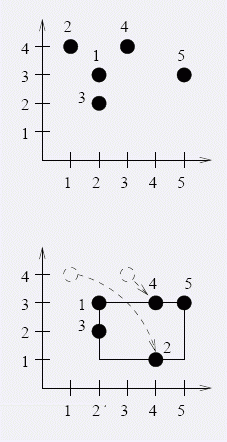
我们把所有的点扔到y=x这条函数的一侧会最优，至于证明，其实十分显然



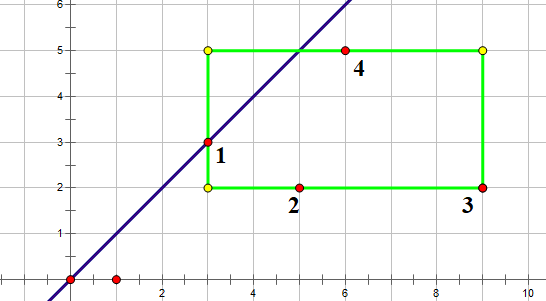
我们考虑如图所示的情况，如果说我的结论是错误的，那么就会有某个点在对称过去后，会使得答案更优。但是我们发现，只要我们挪动了点2和点4，点3是需要跟着移动的，否则答案必然会不优。

但是我们发现，移动了点之后，虽然能使宽度减少，但是会使得高度增加；或者是使得高度减少，宽度增加，而且增加减少值是一样的！更重要的是，点3的移动还会使得答案变得不优。

因此我们可以知道，只要将所有点移动到y=x的一侧，答案必然是最优的，如果有某些点在另一边，一定不会使答案更优。

那么第二个答案呢，我们枚举两个矩形就好了，如下



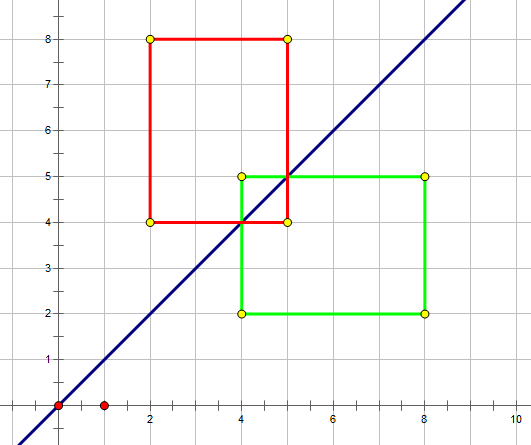
如果只是这样子枚举的话，那么祝你WA的愉快



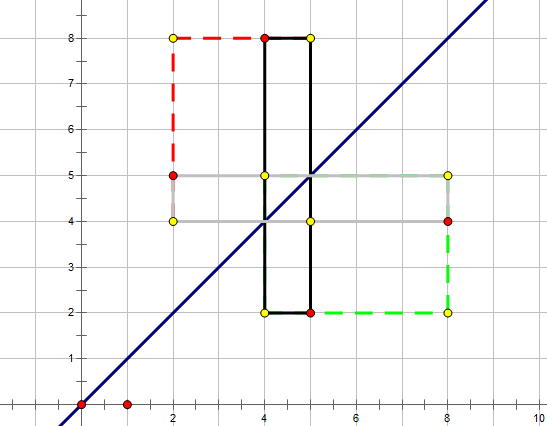
我们还需要枚举黑色和灰色两个矩形，至于为什么，我给你三个点，你自己体会下：(4,2),(5,6),(8,4)，然后(8,4)这个点权值最小

上面所给的4个矩形周长都是一样的，所以都需要枚举

(ps:原题题面还要求输出哪些点被搬动了，然后碰到一堆权值相等的点，又没有spj……所以题面改了)

/*program from Wolfycz*/
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define inf 0x7f7f7f7f
using namespace std;
typedef long long ll;
typedef unsigned int ui;
typedef unsigned long long ull;
inline int read(){
	int x=0,f=1;char ch=getchar();
	for (;ch<'0'||ch>'9';ch=getchar())	if (ch=='-')    f=-1;
	for (;ch>='0'&&ch<='9';ch=getchar())	x=(x<<1)+(x<<3)+ch-'0';
	return x*f;
}
inline void print(int x){
	if (x>=10)     print(x/10);
	putchar(x%10+'0');
}
const int N=1e6;
struct S1{
	int x,y,w;
	void join(int _x,int _y,int _w){x=_x,y=_y,w=_w;}
}A[N+10];
int n,Ans=inf;
void work(int l,int r,int d,int u){
	int res=0;
	for (int i=1;i<=n;i++){//O(n)即可
		int x=A[i].x,y=A[i].y;
		if (l<=x&&x<=r&&d<=y&&y<=u)	continue;
		if (l<=y&&y<=r&&d<=x&&x<=u)	res+=A[i].w;
		else	return;
	}
	Ans=min(Ans,res);
}
int main(){
	n=read();
	int L=inf,R=-inf,U=-inf,D=inf;
	for (int i=1;i<=n;i++){
		int x=read(),y=read(),z=read();
		A[i].join(x,y,z);
		int Min=min(x,y),Max=max(x,y);//挪到同一侧
		L=min(L,Max),R=max(R,Max),U=max(U,Min),D=min(D,Min);
	}
	//做四遍
	work(L,R,D,U);
	work(L,U,D,R);
	work(D,R,L,U);
	work(D,U,L,R);
	printf("%lld %d\n",2ll*(R-L+U-D),Ans);
	return 0;
}