搜索--P1101 单词方阵

题目描述

给一n×n的字母方阵，内可能蕴含多个“yizhong”单词。单词在方阵中是沿着同一方向连续摆放的。摆放可沿着 8 个方向的任一方向，同一单词摆放时不再改变方向，单词与单词之间可以交叉,因此有可能共用字母。输出时，将不是单词的字母用*代替，以突出显示单词。例如：

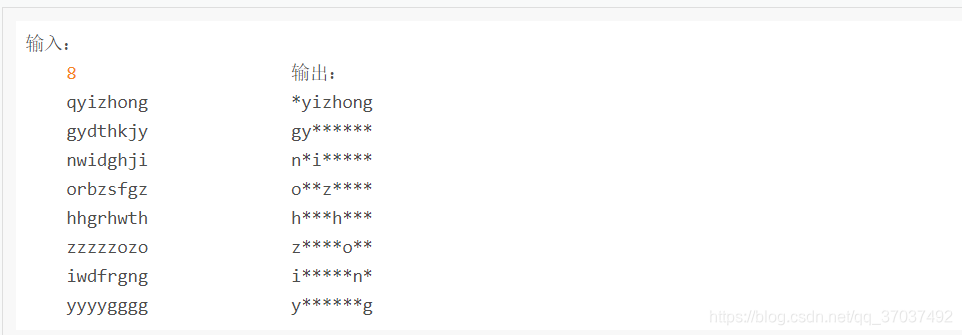
输入输出格式

输入格式：

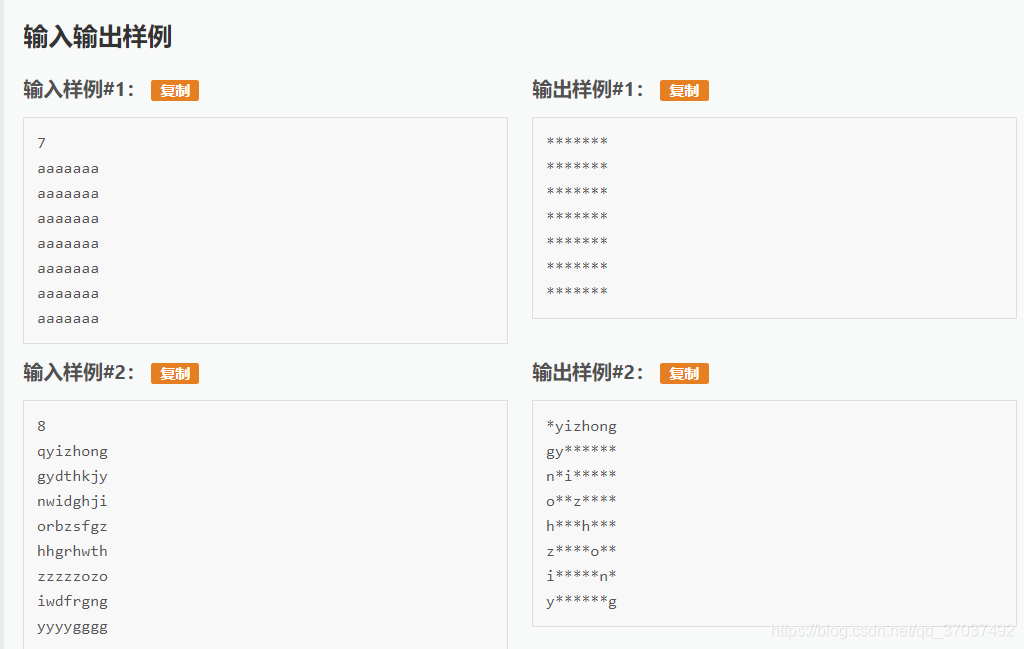
第一行输入一个数n。(7≤n≤100)。

第二行开始输入n×n的字母矩阵。

输出格式：

突出显示单词的n×n矩阵。

AC1（以当前所在位置为判断标准）

之前做的搜索，一维上默认就一个方向，二维上可以上下左右，其实就是任意方向，但是本题的方向只能是一条线上的。所以用上一篇走迷宫的搜索是走不通的。

带搜索方向的dfs。方向作为参数传入dfs，可以使用数组提前存储对应方向，1-8散列到对应方向。最后如何保存轨迹呢？设置一个同等大小的二维字符串数组，注意字符数组的默认填充是空（\0），有结束的id（x,y）和方向，逆推就可以了。

结束条件：使用深度depth作为是否成功的标志，字符串yizhong的长度为7，这里设置如果深度为8则看做搜索成功。

搜索条件：如果当前索引没有越界且等于对应的字符，进行下一层的索引，缺点，因为y已经判断过了，所以这里又进行了一次判断 。如果直接对下一层进行判断会少一些操作，同时判断结束条件的depth应为7，对应的解法在AC2

#include<cstdio>
#include<cmath>
using namespace std;
int N;
char strs[101][101];
char ans[101][101];
//8个方向
int xs[8]={1,-1,0,0,1,-1,1,-1};
int ys[8]={0,0,1,-1,1,-1,-1,1};
//标识
char flag[9]=" yizhong";
int num = 0;
void dfs(int i,int j,int depth,int k){
    //结束条件
    if(depth==8){
        for (int l = 7; l > 0; --l) {
            i-=ys[k];
            j-=xs[k];
            ans[i][j]=strs[i][j];//从g开始
        }
        return;
    }
    if(i<0||j<0||i>N-1||j>N-1){
        return;
    }
    char is = strs[i][j];
    //判断是否为空，当前字符是否符合
    if(flag[depth]==is)
        dfs(i+ys[k],j+xs[k],depth+1,k);
}
int main() {
    scanf("%d", &N);
    int temp = 0;
    while (temp < N) {
        scanf("%s", &strs[temp++]);
    }
    for (int l = 0; l < N; ++l) {
        for (int i = 0; i < N; ++i) {
            ans[l][i]='*';
        }
    }
    for (int i = 0; strs[i][0] !='\0'; ++i) {
        for (int j = 0; strs[i][j] !='\0'; ++j) {
            if(strs[i][j]=='y'){
                dfs(i,j,1,0);
                dfs(i,j,1,1);
                dfs(i,j,1,2);
                dfs(i,j,1,3);
                dfs(i,j,1,4);
                dfs(i,j,1,5);
                dfs(i,j,1,6);
                dfs(i,j,1,7);
            }
        }
    }
    for (int k = 0; k < N; ++k) {
        printf("%s\n",ans[k]);
    }
    return 0;
}

AC2（以下一步为判断标准，更清晰）

#include<cstdio>
#include<cmath>
using namespace std;
int N;
char strs[101][101];
char ans[101][101];
//8个方向
int xs[8]={1,-1,0,0,1,-1,1,-1};
int ys[8]={0,0,1,-1,1,-1,-1,1};
//标识
char flag[9]=" yizhong";
void dfs(int i,int j,int depth,int k){
    //结束条件
    if(depth==7){
        for (int l = 7; l > 0; --l) {
            ans[i][j]=strs[i][j];//从g开始
            i-=ys[k];
            j-=xs[k];
        }
        return;
    }
    if(i+ys[k]<0||j+xs[k]<0||i+ys[k]>N-1||j+xs[k]>N-1){
        return;
    }
    char next =strs[i+ys[k]][j+xs[k]];
    //判断下一个字符是否符合
    if(flag[depth+1]==next)
        dfs(i+ys[k],j+xs[k],depth+1,k);
}
int main() {
    scanf("%d", &N);
    int temp = 0;
    while (temp < N) {
        scanf("%s", &strs[temp++]);
    }
    for (int l = 0; l < N; ++l) {
        for (int i = 0; i < N; ++i) {
            ans[l][i]='*';
        }
    }
    for (int i = 0; strs[i][0] !='\0'; ++i) {
        for (int j = 0; strs[i][j] !='\0'; ++j) {
            if(strs[i][j]=='y'){
                dfs(i,j,1,0);
                dfs(i,j,1,1);
                dfs(i,j,1,2);
                dfs(i,j,1,3);
                dfs(i,j,1,4);
                dfs(i,j,1,5);
                dfs(i,j,1,6);
                dfs(i,j,1,7);
            }
        }
    }
    for (int k = 0; k < N; ++k) {
        printf("%s\n",ans[k]);
    }
    return 0;
}