我学到的treap

到目前为止，平衡树应该是我学过的数据结构里面最难的一个了。（顺便贴上一个我认为treap讲解的比较好的博客https://blog.csdn.net/u014634338/article/details/49612159）

此篇博客只会讲解treap平衡树中较为关键的操作。

前情提要

siz：这里的含义是节点u以下含u有多少数的个数

son[][]：第一维表示当前点，第二维记录当前点的左孩子和右孩子

cnt：储存在节点u中，相同元素的数的个数

key：数据给定的值

ran：随机值（主要用于堆操作）

插入

void insert(int &k,int x)
{
    if (k==)
    {
        k=++num;
        cnt[k]=;
        key[k]=x;
        ran[k]=rand();
        siz[k]=;
        return;
    }
    else if (key[k]==x)
    {
        cnt[k]++;
        siz[k]++;
        return;
    }
    int op=(x>key[k]);
    insert(son[k][op],x);
    if (ran[son[k][op]]<ran[k]) rotate(k,!op);
    pushup(k);
}

插入操作一开始先在树里面递归找有没有相同的点，如果有，直接相同元素的个数+1；如果没有，再到叶子节点里面加上去，但是如果直接这么加了的话，树很容易会退化成链，于是这时候要借鉴堆的性质了。堆的形状十分“平衡”，相对于一颗什么都没优化过的树。由于我们都给了结点一个随机值，所以我们按照这个随机值来进行堆操作（大根堆小根堆都行），但是问题来了，堆和平衡树的性质不会有冲突吗？有冲突确实。以小根堆为例，一个左右都比根大，另一个左小右大，那怎么能够把两者的性质结合在一起呢？

(以下图解由开头推荐博客里面引用，侵删)

先来看看图解：

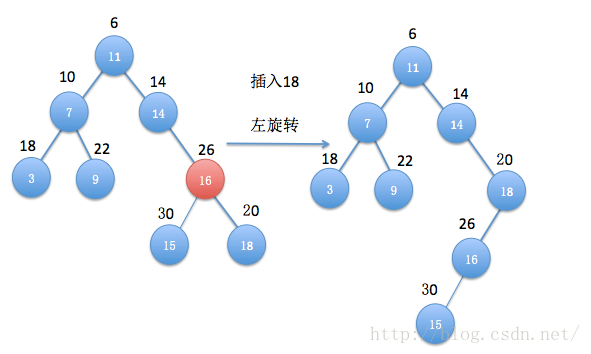
插入值为18，优先级为20的结点后，违反了最小堆的定义，因此要进行调整，把优先级小的往上提，也就是小的优先级插入的是右子树，那么需要进行左旋转，这里进行一次旋转过后就OK了。

同样，这种情况左旋转，旋转后发现还是不满足最小堆的定义，并且小优先级的结点在左子树，所以还需要进行右旋转，如下图所示:

右旋后，很遗憾还是不行，还需要左旋：

OK，终于完成，插入一个数据，也许要进行多次旋转，不过也仅仅是左旋或者右旋而已。

我们由此看到当我们要把两者精华揉在一起时，关键的关键，即是旋转操作，既能维护堆，又能维护平衡树。但是一开始，笔者想到一个问题，仅仅用rand函数随机出来一个值来做为维护堆的依据，是不是有点太草率了，难道不会因为种种原因，而导致随机出来的值特别的奇怪？运行时间不就有不确定性？

以洛谷模板题3369为例，可见每次运行时间只在320ms左右，还算是可以接受的。

删除

分3种情况：

1 不存在这个数，结束

2 存在这个数，而且不止一个，直接递归寻找，然后cnt数组减1

3 存在这个数，但是只有一个，那么这个时候就很烦人了。需要经过一系列的左旋右旋操作，把此结点扔到叶子节点的位置，然后删掉。那么问题来了，如果这个点同时拥有左孩子和右孩子，什么时候左旋什么时候右旋呢？前面我们有介绍了随机值这个东西来维护堆，我们如果要删去一个结点，就一定要让这棵树始终保持堆的性质，因此我们在考虑左旋还是右旋时，先比较两者的随机值的大小，以小根堆为例，如果左边的随机值比右边的小，那么左孩子就应该与当前要删去的结点换一个位置，即左旋，在把删去的结点扔到更下一层的同时，保证了堆和平衡树的性质。

void _delete(int &k,int x)
{
    if (k==) return;
    if (x!=key[k])
    {
        int op=(x>key[k]);
        _delete(son[k][op],x);
        pushup(k);
        return;
    }
    if (cnt[k]>)
    {
        cnt[k]--;
        siz[k]--;
        pushup(k);
        return;
    }
    if (!son[k][]&&son[k][])
    {
        rotate(k,);
        _delete(son[k][],x);
    }
    else if (son[k][] && !son[k][])
    {
        rotate(k,);
        _delete(son[k][],x);
    }
    else if (!son[k][] && !son[k][])
    {
        cnt[k]--;
        siz[k]--;
        if (cnt[k]==) k=;
    }
    else
    {
        int op=(ran[son[k][]]>ran[son[k][]]);
        rotate(k,!op);
        _delete(son[k][!op],x);
    }
    pushup(k);
}

旋转

void rotate(int &x,int op)
{
    int p=son[x][!op];
    son[x][!op]=son[p][op];
    son[p][op]=x;
    pushup(x);
    pushup(p);
    x=p;
}

这个大多数博客都有讲，而且把其视为最重要的操作，其实在我看来，我们只要把旋转操作视为交换两个点的位置就行，只不过由于是颗平衡树，交换位置会导致“牵一发而动全身”，才显得比较复杂。这里就不再过多阐述旋转的操作。

总结

平衡树花了我很多时间去学习，可能是由于每个人码风不同，或是我认为的难点大多数博主都一笔带过，学习的过程就有点艰苦......。但是当你完全理解之后，才会体会到平衡树的魅力。

最后附上洛谷模板题的代码（因为我是靠看别人的代码来逐渐弄懂的，所以可能和别人的代码有点雷同）

#include <bits/stdc++.h>
#define maxn 1000010
#define inf 0x3f3f3f3f
using namespace std;
int key[maxn],cnt[maxn],ran[maxn],siz[maxn],son[maxn][],op,n,num=,x,root=;
void pushup(int x)
{
    siz[x]=siz[son[x][]]+siz[son[x][]]+cnt[x];
}
void rotate(int &x,int op)
{
    int p=son[x][!op];
    son[x][!op]=son[p][op];
    son[p][op]=x;
    pushup(x);
    pushup(p);
    x=p;
}
void insert(int &k,int x)
{
    if (k==)
    {
        k=++num;
        cnt[k]=;
        key[k]=x;
        ran[k]=rand();
        siz[k]=;
        return;
    }
    else if (key[k]==x)
    {
        cnt[k]++;
        siz[k]++;
        return;
    }
    int op=(x>key[k]);
    insert(son[k][op],x);
    if (ran[son[k][op]]<ran[k]) rotate(k,!op);
    pushup(k);
}
void _delete(int &k,int x)
{
    if (k==) return;
    if (x!=key[k])
    {
        int op=(x>key[k]);
        _delete(son[k][op],x);
        pushup(k);
        return;
    }
    if (cnt[k]>)
    {
        cnt[k]--;
        siz[k]--;
        pushup(k);
        return;
    }
    if (!son[k][]&&son[k][])
    {
        rotate(k,);
        _delete(son[k][],x);
    }
    else if (son[k][] && !son[k][])
    {
        rotate(k,);
        _delete(son[k][],x);
    }
    else if (!son[k][] && !son[k][])
    {
        cnt[k]--;
        siz[k]--;
        if (cnt[k]==) k=;
    }
    else
    {
        int op=(ran[son[k][]]>ran[son[k][]]);
        rotate(k,!op);
        _delete(son[k][!op],x);
    }
    pushup(k);
}
int rank(int k,int x)
{
    if (k==) return ;
    if (key[k]==x) return siz[son[k][]]+;
    if (key[k]>x) return rank(son[k][],x);
    return siz[son[k][]]+cnt[k]+rank(son[k][],x);
}
int find(int k,int x)
{
    if (k==) return ;
    if (siz[son[k][]]>=x) return find (son[k][],x);
    else if (siz[son[k][]]+cnt[k]<x) return find (son[k][],x-siz[son[k][]]-cnt[k]);
    else return key[k];
}
int lowerbound(int k,int x)
{
    if (k==) return -inf;
    if (key[k]>=x) return lowerbound(son[k][],x);
        else return max(key[k],lowerbound(son[k][],x));
}
int upperbound(int k,int x)
{
    if (k==) return inf;
    if (key[k]<=x) return upperbound(son[k][],x);
        else return min(key[k],upperbound(son[k][],x));
}
int main()
{
    cin>>n;
    while (n--)
    {
        scanf("%d%d",&op,&x);
        switch(op)
        {
            case :insert(root,x);break;
            case :_delete(root,x);break;
            case :printf("%d\n",rank(root,x));break;
            case :printf("%d\n",find(root,x));break;
            case :printf("%d\n",lowerbound(root,x));break;
            case :printf("%d\n",upperbound(root,x));break;
        }
    }
    return ;
 } 

splay

相较于treap来说，splay不需要任何额外的内容，只要保证一个splay和旋转的操作即可，而所谓的splay操作，就是通过旋转把一个点向上转到目标点的操作。

模板：https://blog.csdn.net/clove_unique/article/details/50636361

懒人版平衡树

其实C++STL基本容器里面有很多好东西，常见的就是vector、set、map等等，这里用到的是vector来实现平衡树功能

代码极短

#include <bits/stdc++.h>
#define debug freopen("r.txt","r",stdin)
#define mp make_pair
#define ri register int
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
const int maxn = 4e5+;
const int INF = 0x3f3f3f3f;
const int mod = ;
inline ll read(){ll s=,w=;char ch=getchar();
while(ch<''||ch>''){if(ch=='-')w=-;ch=getchar();}
while(ch>=''&&ch<='') s=s*+ch-'',ch=getchar();
return s*w;}
ll qpow(ll p,ll q){return (q&?p:)*(q?qpow(p*p%mod,q/):)%mod;}
vector<int>v;
int t,opt,x;
int main()
{
    t=read();
    while(t--)
    {
        opt=read(),x=read();
        if(opt==) v.insert(lower_bound(v.begin(),v.end(),x),x);
        if(opt==) v.erase (lower_bound(v.begin(),v.end(),x));
        if(opt==) printf("%d\n",lower_bound(v.begin(),v.end(),x)-v.begin()+);
        if(opt==) printf("%d\n",v[x-]);
        if(opt==) printf("%d\n",v[lower_bound(v.begin(),v.end(),x)-v.begin()-]);
        if(opt==) printf("%d\n",v[upper_bound(v.begin(),v.end(),x)-v.begin()]);
    }
    return ;
}

但是可能会被卡数据