HDU6035 Colorful Tree

题目链接：https://vjudge.net/problem/HDU-6035

题目大意：

　　多样例输入。

　　对于每一个样例，给出 n \((2 \le n \le 200000)\) 个结点的一棵树，各个节点都有各自的颜色 \(c_i  (1 \le c_i \le n)\)，树上任意两点之间的路径的权值为该路径经过的不同颜色的结点数，求树上所有两点路径的权值之和。

知识点：　　树、DFS

解题思路：

　　求树上所有的两点路径的权值之和，可以转化为求各个颜色在各条路径中的贡献值（即该颜色能够为树上的各条路径增加的权值的总和，也可以理解成是该颜色在多少条路径中出现）。但是，并没有非常好的方法可以直接求出这个总的贡献值，于是，我们可以反过来求：各个颜色在多少条路径中没有出现。

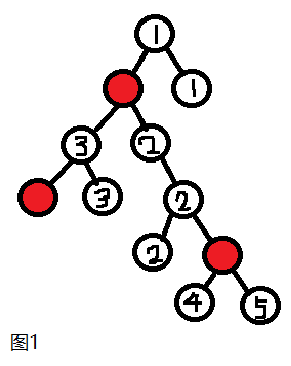
　　如图1所示，树上所有的红色结点将整棵树分成了 5 个联通块（笔者已用 1~5 标出），则这五个联通块里面的所有路径显然都没有经过红色结点。其实这些联通块也可以看成是一棵子树，对于一棵有 n 个结点的树，树上所有路径数为 \(\frac{n(n-1)}{2}\) ¹

　　那么，我们所要求的答案其实就是\(\frac{NumberOfColors \times n \times (n-1)}{2}\) - 没有经过各个颜色的所有路径数

　　对于每一种颜色，没有经过该种颜色的路径可以分成两类：

　　1、从树根以下，到第一次接触颜色点之前的这一联通块的路径（如图1中的第1块）；

　　2、颜色点之间和颜色点以下直到叶子的联通块（如图1中的第2~5块）。

　　只要算出这两种路径的总数，即可求出答案，但此题的实现并不简单，请看代码及注释：

AC代码：

 #include <cstdio>
 #include <vector>
 #include <set>

 using namespace std;
 typedef long long ll;
 const int maxn=+;

 int color[maxn];//记录各个结点的颜色
 ll sum[maxn];//精髓所在
 ll sizes[maxn];//记录各个结点以下的结点数
 vector<int> tree[maxn];//记录树
 set<int> col;
 ll ans;
 void find_size(int fa,int gfa){//找出各点的 sizes[i]
     sizes[fa]=;
     for(int i=;i<tree[fa].size();i++){
         if(tree[fa][i]==gfa)    continue;
         find_size(tree[fa][i],fa);
         sizes[fa]+=sizes[tree[fa][i]];
     }
 }
 void find_ans(int fa,int gfa){
     ll tmp=;
     if(sum[color[fa]]!=){
 //此处 sum[color[fa]] 记录的是目前已知的从各个分枝的第一个颜色为 color[fa] 的点到叶子的结点数，那么当最后求出这个值以后，上文提及的第一类路径的结点数即为 n-sum[i]
         tmp=sum[color[fa]];
         sum[color[fa]]=;
 /*      *****************       */
     }
     for(int i=;i<tree[fa].size();i++){
         if(tree[fa][i]==gfa)    continue;
         find_ans(tree[fa][i],fa);
 //此处sum[color[fa]]用于求从 tree[fa][i] 这个结点出发到下一个颜色为 color[fa] 或者叶子的联通块的结点数
 //请注意上下两处划线处的代码
         ans-=(sizes[tree[fa][i]]-sum[color[fa]])*(sizes[tree[fa][i]]-sum[color[fa]]-)/;
         sum[color[fa]]=;
 /*      *****************       */
     }sum[color[fa]]=sizes[fa]+tmp;
 }
 int main(){
     int n,a,b;
     int kase=;
     while(scanf("%d",&n)==){
         col.clear();
         for(int i=;i<=n;i++){
             sum[i]=;
             tree[i].clear();
         }
         for(int i=;i<=n;i++){
             scanf("%d",&color[i]);
             col.insert(color[i]);
         }
         ans=(ll)col.size()*n*(n-)/;
         for(int i=;i<n;i++){
             scanf("%d%d",&a,&b);
             tree[a].push_back(b);
             tree[b].push_back(a);
         }find_size(,);
         find_ans(,);
         set<int>::iterator pt=col.begin();
         for(;pt!=col.end();pt++){
             int cl=*pt;
             ans-=(n-sum[cl])*(n-sum[cl]-)/;
         }
         printf("Case #%d: %lld\n",kase++,ans);
     }return ;
 }

　　

　　

1、n(n-1)/2——此处的公式可能会挂，原因不明......