NEKO's Maze Game - Codeforces 题解

题目

NEKO#ΦωΦ has just got a new maze game on her PC!

The game's main puzzle is a maze, in the forms of a \(2×n\) rectangle grid. NEKO's task is to lead a Nekomimi girl from cell \((1,1)\) to the gate at \((2,n)\) and escape the maze. The girl can only move between cells sharing a common side.

However, at some moments during the game, some cells may change their state: either from normal ground to lava (which forbids movement into that cell), or vice versa (which makes that cell passable again). Initially all cells are of the ground type.

After hours of streaming, NEKO finally figured out there are only q such moments: the i-th moment toggles the state of cell \((ri,ci)\) (either from ground to lava or vice versa).

Knowing this, NEKO wonders, after each of the q moments, whether it is still possible to move from cell \((1,1)\) to cell \((2,n)\) andwithout going through any lava cells.

Although NEKO is a great streamer and gamer, she still can't get through quizzes and problems requiring large amount of Brain Power. Can you help her?

\(2×n\)的迷宫，从\((1,1)）\)出发到\((2,n)\)，初始时全部的都是地面，每次询问会把一个地面给变成熔浆，熔浆变成地面，熔浆不能通过，问是否可以走到。

输入格式

The first line contains integers$ n, q (2≤n≤105, 1≤q≤105)$.

The i-th of q following lines contains two integers \(ri, ci (1≤ri≤2, 1≤ci≤n)\), denoting the coordinates of the cell to be flipped at the i-th moment.

It is guaranteed that cells \((1,1)\) and \((2,n)\) never appear in the query list.

第一行两个整数\(n,q\).

接下来又q行,第\(i\)行包括两个整数,\(ri, ci (1≤ri≤2, 1≤ci≤n)\),表示在第i个时刻要翻转的单元格的坐标.

确保单元格\((1,1)\)和\((2,n)\)永远不会出现在查询列表中。

输出格式

For each moment, if it is possible to travel from cell \((1,1)\) to cell \((2,n)\), print "Yes", otherwise print "No". There should be exactly q answers, one after every update.

对于每个时刻，如果可以从单元格\((1,1)\)到单元格\((2,n)\)，则打印"Yes"，否则打印"No",有q个答案，每行输入对应一行输出.

输入样例

5 5
2 3
1 4
2 4
2 3
1 4

输出样例

Yes
No
No
No
Yes

题解

这道题的大概思路还是挺好想的,大概就是每次输入的时候记录下挡路的"单元"

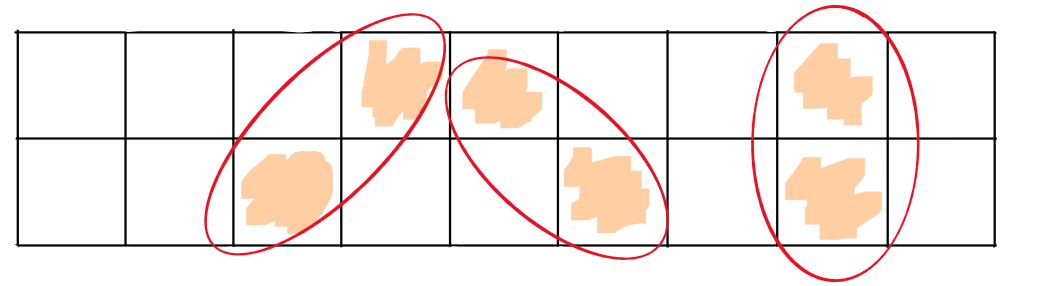
上图用圈出来的部分都是一个单元,可以阻挡玩家通过,如果整个地图只有一个熔浆单元格,显然是不足以构成一个单元,至少两个(上面三种情况)才可以构成.

那么思路就有了,如果在反转的时候对面三个格子已经有了熔浆单元,单元的数量加一.

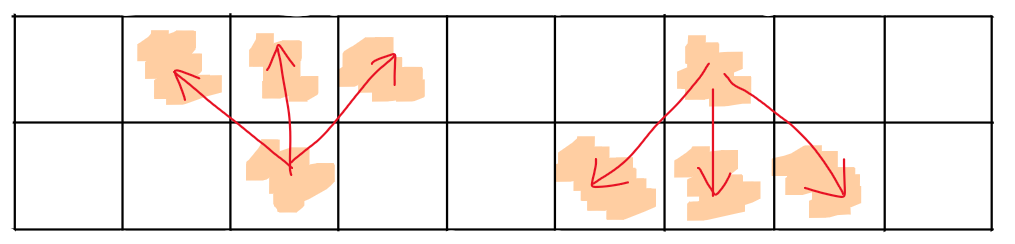
在反转的时候,如果对面已经有了熔浆单元,说明这个格子在从地面到熔浆的过程中,单元的数量增加了,那么反转的时候自然要减回去.

还有一个小技巧,为了方便的表示"对面的x坐标",有三种方式:

1. 使用if语句,例如#define o(x) ((x)==1?2:1),o(x)表示对面的横坐标

2. 因为\(x\)坐标有\(1\)和\(2\)两种情况,那么用3去减就可以了,同样可以推广,如果一个变量只有两个值的可能性\(a\)和\(b\),使用同一种运算在a和b之间转化的方式就是\(a+b-x\),例如当\(x\)为\(a\),\(a+b-a=b\);当\(x\)为\(b\),\(a+b-b=a\),在这道题中,\(3-x\)表示对面的横坐标.

3. 有没有感觉这种运算像取反操作?我们只要稍作修改,就可以使用取反来操作.在输入之后立刻x--,然后就可以用!x表示对面的横坐标,这种操作好在可以少开\(10^5\)大小的数组.

代码

#include <cstdio>
int vis[2][100005];
int n, q, x, y, ans;
int main() {
    scanf("%d%d", &n, &q);
    while (q--) {
        scanf("%d%d", &x, &y);
        x--;
        if (vis[x][y]) {
            if (vis[!x][y]) ans--;
            if (vis[!x][y + 1] && y + 1 <= n) ans--;  //注意边界
            if (vis[!x][y - 1] && y - 1 >= 1) ans--;
        } else {
            if (vis[!x][y]) ans++;
            if (vis[!x][y + 1] && y + 1 <= n) ans++;
            if (vis[!x][y - 1] && y - 1 >= 1) ans++;
        }
        vis[x][y] = !vis[x][y];
        printf("%s\n", ans ? "No" : "Yes");
    }
}