面试中很值得聊的二叉树遍历方法——Morris遍历

Morris遍历

通过利用空闲指针的方式，来节省空间。时间复杂度O(N)，额外空间复杂度O(1)。普通的非递归和递归方法的额外空间和树的高度有关，递归的过程涉及到系统压栈，非递归需要自己申请栈空间，都具有O(N)的额外空间复杂度。

Morris遍历的原则:

1. 假设当前节点为cur，

2. 如果cur没有左孩子，cur向右移动，cur = cur.right

3. 如果cur有左孩子，找到左子树上最右的节点mostRight

　　3.1 如果mostRight.right == null，令mostRight.right = cur，cur向左移动，cur = cur.left

　　3.2 如果mostRight.right == cur，令mostRight.right = null，cur向右移动，cur = cur.right

4. 如果cur == null 停止遍历

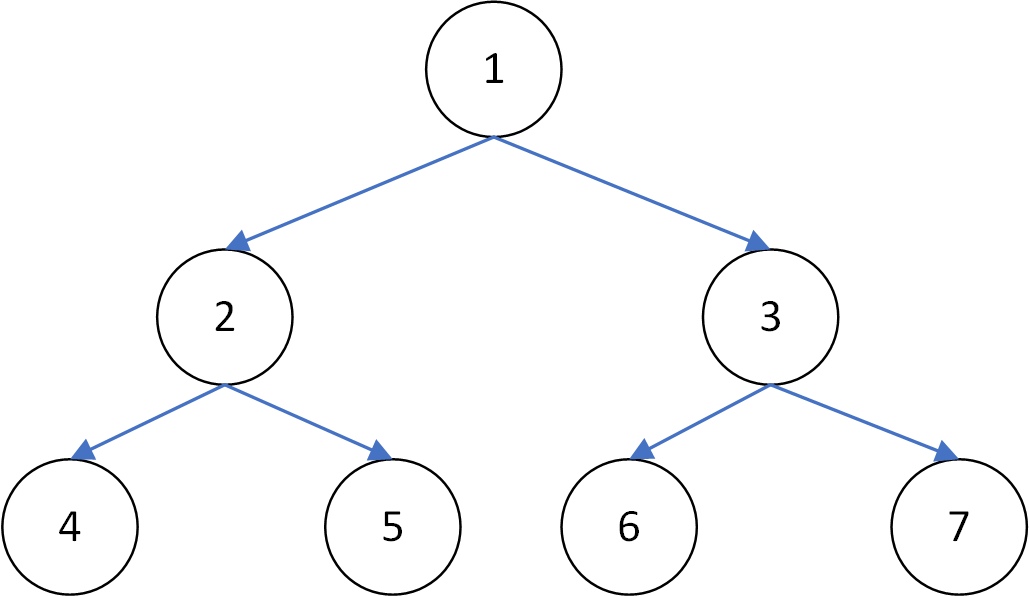
Morris：1242513637

     public static void morris(TreeNode head){
         if(head == null) return;
         TreeNode cur = head;
         TreeNode mostRight = null;
         while(cur != null){//cur为空遍历停止【4】
             mostRight = cur.left;//是cur左子树上最右的节点
             if(mostRight != null){//有左子树【3】
                 while(mostRight.right != null && mostRight != cur){//mostRight!=cur不加就会绕环循环
                     mostRight = mostRight.right;//找最右节点【3】
                 }
                 if(mostRight.right == null){//第一次来到cur【3.1】
                     mostRight.right = cur;
                     cur = cur.left;
                     continue;//执行循环
                 }else {//mostRight.right = cur第二次来到cur【3.2】
                     mostRight.right = null;
                 }
             }
             cur = cur.right;//没有左子树【2】

         }
     }

所有节点遍历左子树右边界的时间总代价O(N)

基于Morris的先中后序遍历

如果cur有左子树一定能遍历2次，没有左子树只能遍历一次。

先序遍历

Morris：1242513637

Morris先序：1245367

基于Morris的先序遍历，如果一个节点可以到达两次则打印第一次，如果只能到达一次直接打印。

     public static void morrisPre(TreeNode head){
         if(head == null) return;
         TreeNode cur = head;
         TreeNode mostRight = null;
         while(cur != null){//有左子树
             mostRight = cur.left;
             if(mostRight != null){
                 while(mostRight.right != null && mostRight != cur){
                     mostRight = mostRight.right;
                 }
                 if(mostRight.right == null){//第一次来到左子树
                     System.out.println(cur.val);//打印
                     mostRight.right = cur;
                     cur = cur.left;
                     continue;
                 }else {
                     mostRight.right = null;
                 }
             }else{
                 System.out.println(cur.val);//没有左子树 只会遍历一次
             }
             cur = cur.right;
         }
     }

中序遍历

Morris：1242513637

Morris中序：4251637

基于Morris的中序遍历，如果一个节点可以到达两次则打印第二次，如果只能到达一次直接打印。

     public static void morrisIn(TreeNode head) {
         if(head == null) return;
         TreeNode cur = head;
         TreeNode mostRight = null;
         while(cur != null){
             mostRight = cur.left;
             if(mostRight != null){
                 while(mostRight.right != null && mostRight != cur){
                     mostRight = mostRight.right;
                 }
                 if(mostRight.right == null){
                     mostRight.right = cur;
                     cur = cur.left;
                     continue;
                 }else {
                     mostRight.right = null;
                 }
             }
             //没有左树跳过if直接打印，有左树第二次来到cur退出循环打印
             System.out.println(cur.val);
             cur = cur.right;
         }
     }

后序遍历

Morris：1242513637

Morris先序：4526731

基于Morris的后序遍历，如果一个节点可以到达两次则第二次到达时逆序打印左树的右边界，单独逆序打印整棵树的右边界。

（1）逆序右边界（等同于单链表的逆序）

       public static TreeNode reverseEdge(TreeNode from) {
         TreeNode pre = null;
         TreeNode next = null;
         while(from != null){
             next = from.right;
             from.right = pre;
             pre = from;
             from = next;
         }
         return pre;
     }

（2）逆序打印以head为头节点的右边界。

     public static void printRightEdge(TreeNode head) {
         TreeNode tail = reverseEdge(head);//逆转右边界
         TreeNode cur = tail;
         while(cur != null){
             System.out.println(cur.val + " ");
             cur = cur.right;
         }
         reverseEdge(tail);//逆转回去 恢复原树
     }

（3）在Morris遍历中按时机打印。

     public static void morrisPost(TreeNode head){
         if(head == null) return;
         TreeNode cur = head;
         TreeNode mostRight = null;
         while(cur != null){
             mostRight = cur.left;
             if(mostRight != null){
                 while(mostRight.right != null && mostRight != cur){
                     mostRight = mostRight.right;
                 }
                 if(mostRight.right == null){
                     mostRight.right = cur;
                     cur = cur.left;
                     continue;
                 }else {//第二次达到 逆序打印左子树的右边界
                     mostRight.right = null;
                     printRightEdge(cur.left);
                 }
             }
             cur = cur.right;
         }
         //最后退出循环之后，单独打印整棵树的右边界
         printRightEdge(head);
     }

Morris遍历的应用

如何判断一棵树是否是搜索二叉树？

中序遍历升序就是搜索二叉树。

     public static boolean isBST(TreeNode head){
         if(head == null) return true;
         TreeNode cur = head;
         TreeNode mostRight = null;
         int preValue = Integer.MIN_VALUE;//上一次得到的值
         while(cur != null){
             mostRight = cur.left;
             if(mostRight != null){
                 while(mostRight.right != null && mostRight != cur){
                     mostRight = mostRight.right;
                 }
                 if(mostRight.right == null){
                     mostRight.right = cur;
                     cur = cur.left;
                     continue;
                 }else {
                     mostRight.right = null;
                 }
             }
             //中序遍历的操作时机在这里 所以在这里进行判断
             if(cur.val <= preValue){//没有递增
                 return false;
             }
             preValue = cur.val;
             cur = cur.right;
         }
         return true;
     }

总结

树型DP问题的套路：定义一个类收集树的信息，定义一个递归函数，递归地收集左子树的信息和右子树的信息，再整合得到以当前节点为根的树的信息。

什么时候用树型DP什么时候用Morris遍历？

当必须得到左树的信息和右树的信息后，再在当前节点整合二者信息后做出判断则用树型DP是最优解。

当不需要整合左树和右树信息的时候，可以用树型DP，但是Morris是最优解。