Andrew 算法求凸包

Andrew 算法求凸包

参考资料：

右手定则(baidu.com)

内积和外积 - OI Wiki (oi-wiki.org)

• \(a\) 与 \(b\) 相对位置
  • \(b\) 在 \(a\) 的逆时针方向: \(a \times b>0\)
  • 顺负逆正（其实就是高中数学对于正负角的定义）

凸包 - OI Wiki (oi-wiki.org)

• 伪代码

while(右旋){

标记原来的栈顶为不在凸包上

}

标记新点在栈顶上

加入栈中

• 一般是叉积小于0则不合法（=0是平的，但合法）

二维凸包

定义

凸多边形

凸多边形是指所有内角大小都在 \([0,\pi]\) 范围内的 简单多边形。

凸包

在平面上能包含所有给定点的最小凸多边形叫做凸包。

实际上可以理解为用一个橡皮筋包含住所有给定点的形态。

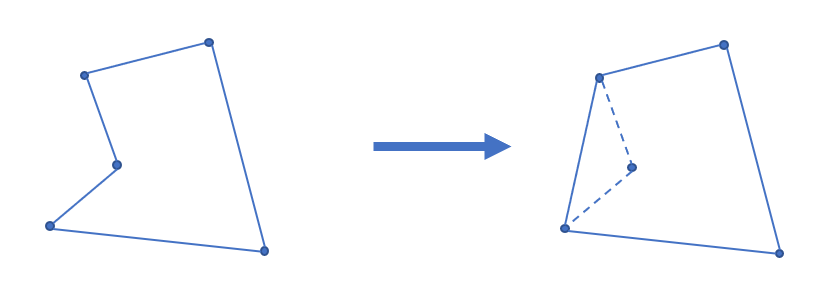
凸包用最小的周长围住了给定的所有点。如果一个凹多边形围住了所有的点，它的周长一定不是最小，如下图。根据三角不等式，凸多边形在周长上一定是最优的。

Andrew 算法求凸包

过程：

1、首先以 \(x\) 为第一关键字, \(y\) 为第二关键字排序

2、显然排序后最小的元素和最大的元素一定在凸包上。而且因为是凸多边形，我们如果从一个点出发逆时针走，轨迹总是「左拐」的，一旦出现右拐，就说明这一段不在凸包上。因此我们可以用一个单调栈来维护上下凸壳。

因为从左向右看，上下凸壳所旋转的方向不同，为了让单调栈起作用，我们首先 升序枚举 求出下凸壳，然后 降序 求出上凸壳。

• 左右旋的判定：叉积的正负（左旋为正角，右旋为负角，0证明是平的一段）

二维凸包模板：Luogu P2742 Fencing the Cows

#include<bits/stdc++.h>
#define F(i,l,r) for(int i(l);i<=r;++i)
#define G(i,r,l) for(int i(r);i>=l;--i)
#define double long double
using namespace std;
using ll = long long;
const int N=1e5+105;
struct node{
	double x,y;
	node operator - (const node &o)const{
		node z=(node){x-o.x,y-o.y};
		return z;
	}
	double operator * (const node &o)const{
		return x*o.y-y*o.x;
	}
	bool operator < (const node &o)const{
		return x==o.x ? y<o.y : x<o.x;
	}
}w[N];
double dis(node a){
	return __builtin_sqrt(a.x*a.x+a.y*a.y);
}
int tp=0,n;
int stk[N<<1];
bool used[N];
double ans=0;
signed main(){
	ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
	cin>>n; F(i,1,n) cin>>w[i].x>>w[i].y;
	sort(w+1,w+n+1);
	stk[++tp]=1;//used不打标记方便最后封闭
	F(i,2,n){
		while(tp>=2 && (w[stk[tp]]-w[stk[tp-1]])*(w[i]-w[stk[tp]])<0) used[stk[tp--]]=0;
		//注意叉积小于0,一定不能写成小于等于！
		used[i]=1;
		stk[++tp]=i;
	}
	G(i,n,1){
		if(used[i]) continue;
		while(tp>=2 && (w[stk[tp]]-w[stk[tp-1]])*(w[i]-w[stk[tp]])<0) used[stk[tp--]]=0;
		used[i]=1;
		stk[++tp]=i;
	}
	F(i,1,tp-1) ans+=dis(w[stk[i+1]]-w[stk[i]]);//凸包周长的求法
	ans+=dis(w[stk[1]]-w[stk[tp]]);
	cout<<fixed<<setprecision(2)<<ans<<"\n";
	return 0;
}