青岛oj集训5

Floyd算法——全源最短路

cerr:标准输出错误流：不会输出到freopen制定的out文件中，而是会输出到错误文件中。

提交上去无论加不加freopen，哪怕是提交到洛谷，也只是比较out文件中的值，而不会管cerr输出的东西

好处：调试的时候用cerr，哪怕忘删调试调试

例题1：传递闭包

floyd可以直接算，但复杂度太高

压缩：用bitset优化

bool：00000001/00000000

bitset：1/0

bool&bool运算时间：O（n）

bitset&bitset：O（n/w）（w是机器字长，一般考试是64，即优化速度快了64倍）

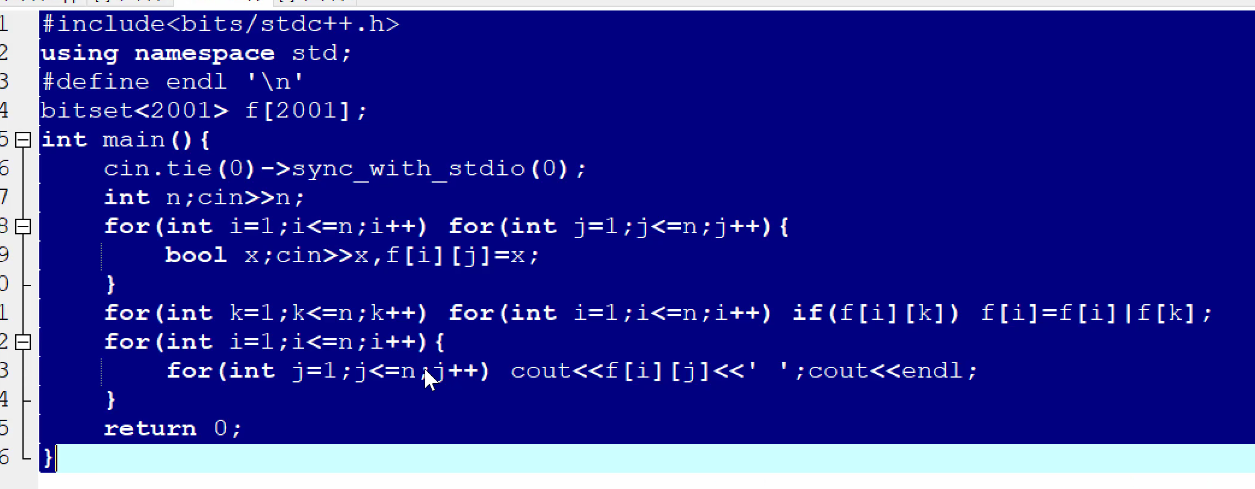
这里看一下这的算法：

假设有一条1-2-3-4的链

f[1]=1100,即能到达12点，到不了34

1:1100    由于这里1能够到达2if(f[i][k])成立，才能用2去更新1的所有可达点

2:1110

————

1:1110

3：0111

————

1:1111

这样经过两轮更新，就能到34了

（p.s：其实实际上不是逮着一个点一直更新它，这样可能有更新不到的情况。实际上是先用一个点去更新所有可达点（先枚举k））

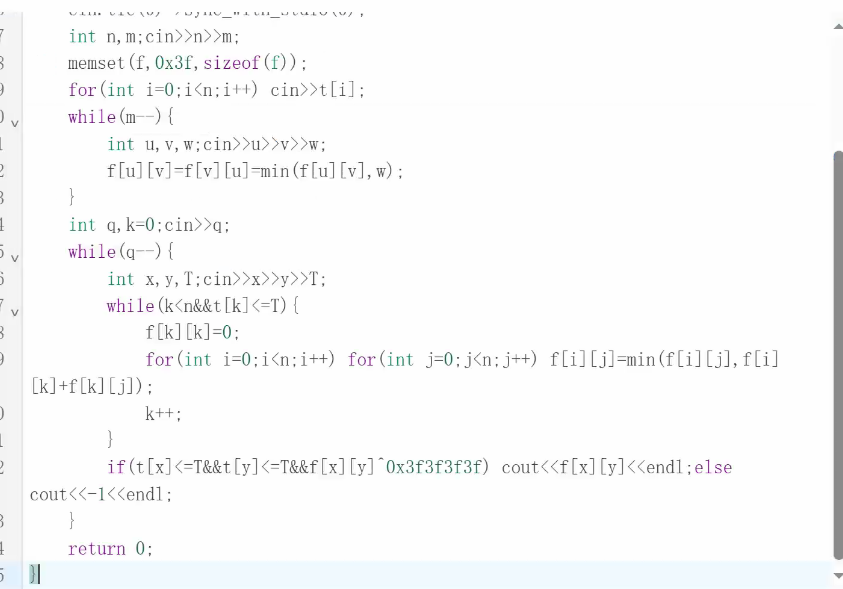
例题二：灾后重建

方法一：把所有讯问离线下来，按照t升序进行回答，在排回去

但是这道题保证了Q次讯问的t是不降的，所以就不用离线下来排序了

而且村庄标号越大，解封时间越晚

所以直接枚举点的标号就是解封顺序

用k来代表目前解封到第几个点了

当k<n时（总共就n个点，想干啥）并且k这个点解封的时间早于讯问时间（那么在它之前所有点都解封了）

那么以新解封的k这个点作为中转点，对所有之前的点进行更新

然后再向后探索一个点，知道新的点不存在或未解封

如果讯问的时间中k已经跑过一遍，就不用再跑一遍，直接用这张最后更新的图输出结果就行

输出时要特判：1.起点终点是否尚未解冻2.起点终点之间是否有连线

例题3：无向图的最小问题

假设这个环上就三个点，那么环得长度就是三个点之间的最短路径和

先跑Floyd

假设这三个顶点分别是ijk，那么最短环就是ij+ik+jk之间的最短路

但是一个例子：1-2-3链

很明显：没有环

但是Floyd会将1-3之间强制加上一条长度为1-2+2-3的边

这样程序就会算出最小环位1-2-3-2-1，很明显，有重边，肯定不行

怎么解决？

既然Floyd会强制改变边，那么我们就把边提前备份出来一边，不让Floyd动不就好啦

等用完了再让Floyd动也不迟

代码中mp表示打死不动，我们备份出来的原边长

f代表我们已经用完了，让Floyd去算完的边长

我们先固定下来一个点k，是这个环路径上经过的所有点中编号最大的那个

再枚举两个互不相同的点ij且比k小

kij的环必须是k到i、j的直接路径+i、j之间的最短路径长度

枚举完所有符合条件的环之后，要以k为中转点对所有点更新f数组

因为k以后再也不可能是k了，只能作为最短路径上的中转点

新的一轮ijk，ki、kj都是mp用的直接距离不会有影响

而ij之间的f数组求的是以所有比k小的的点为中转点的最短路

换句话说，ij这条边你就算走出花来，也不可能经过k点或比k更大的点

这样就可以完美地列举所有环了

（倒数第三行的INT_MAX改为1e8）

例题四：Redistributing Gifts S

把最优性转换成可行性问题，用传递闭包解决

建图，如果u看得上v的礼物，觉得v的礼物比他的好，那么就建一条边u->v

然后先跑一遍传递闭包，求出所有可达点

如果i可以到达j点，那么说明i可以拿到j的礼物

最后就输出每一个奶牛，如果它能拿到愿望清单上的1号礼物，就输出1号（不一定就是礼物1，只是排名最靠前的那个）

如果能，就输出完了broke掉，否则就下一个，直到找到最靠前的（肯定能找到的，毕竟自己到自己要设为可达）

代码吗……嘿嘿，手速慢没截到，要不那个时候的我（不会吧？我的博文还有除我以外的人看？）再补上？嘻嘻……反正坑是填不完的嘛