Web前端入门第 41 问：神奇的 transform 改变元素形状，matrix3d 矩阵变换算法演示

CSS transform 属性中文翻译过来是 变换，始终觉得翻译差那么一点意思。它可以用来改变元素形状，比如旋转、缩放、移动、倾斜等，就是它可以把元素各种拿捏~

transform 特性是在不改变自身尺寸的情况下，对元素进行各种变形，元素自身的文档流位置还是会保留，语言有些空洞，下面看例子。

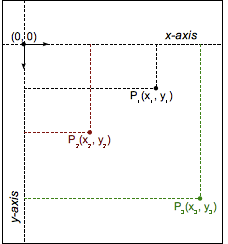
笛卡尔坐标

学习变换之前，先了解一下笛卡尔坐标系，：

在笛卡尔坐标系中，每个 欧氏空间 里的点都由横坐标和纵坐标这两个值来确定。在 CSS（和大部分的计算机图形学）中，原点 (0, 0) 在元素的左上角。每个点都使用数学上的向量符号 (x,y) 来描述。

-- 摘自 MDN

意思就是 CSS 的坐标系都是从元素左上角开始的，与数学的坐标系稍有不同，Y 轴的箭头是相反的！！

transform 的属性值

截至到文章编写时，CSS3 transform 属性值有如下 21 种：

translate() 设置 2D 位移。

translate3d() 设置 3D 位移。

translateX() 设置 X 轴位移。

translateY() 设置 Y 轴位移。

translateZ() 设置 Z 轴位移。

skew() 设置 2D 倾斜。

skewX() 设置水平方向倾斜。

skewY() 设置垂直方向倾斜。

scale() 设置 2D 缩放。

scale3d() 设置 3D 缩放。

scaleX() 设置 3D X 轴缩放。

scaleY() 设置 3D Y 轴缩放。

scaleZ() 设置 3D Z 轴缩放。

rotate() 设置 2D 旋转角度。

rotate3d() 设置 3D 旋转角度。

rotateX() 设置 3D X 轴旋转角度。

rotateY() 设置 3D Y 轴旋转角度。

rotateZ() 设置 3D Z 轴旋转角度。

perspective() 设置 3D 透视，值越大会感觉越远。

---

matrix() 2D 矩阵变换。

matrix3d() 3D 矩阵变换，最底层的矩阵操作方法。

transform 的所有属性值都不会改变元素的自身的文档流位置！

意思就是给元素施加的 transform 仅仅是元素形态上的变化，而不会改变元素自身的位置和大小！！！

3D 立方体

为了看出每种变换的效果，先用 CSS 绘制一个立方体。代码如下：

里面也用到了 transform 属性，可以先不管代码意思，只需要知道我们的目的就是绘制一个立方体出来就行。

<div class="box">
  <section class="cube">
    <div class="face">1</div>
    <div class="face">2</div>
    <div class="face">3</div>
    <div class="face">4</div>
    <div class="face">5</div>
    <div class="face">6</div>
  </section>
</div>
<style>
  .box {
    border: 2px solid rgba(255, 71, 87,0.3);
    margin: 20px 0;
    padding: 20px;
    width: 100px;
    perspective: 800px; /* 透视点距离 */
  }
  .cube {
    width: 100px;
    height: 100px;
    transform-style: preserve-3d; /* 子元素位于 3D 空间中 */
    position: relative;
  }
  .face {
    display: flex;
    align-items: center;
    justify-content: center;
    width: 100%;
    height: 100%;
    position: absolute;
    backface-visibility: visible;
    font-size: 60px;
    color: #fff;
  }
  .face:nth-of-type(1) {
    background: rgba(90, 90, 90, 0.6);
    transform: translateZ(50px);
  }
  .face:nth-of-type(2) {
    background: rgba(0, 161, 210, 0.6);
    transform: rotateY(180deg) translateZ(50px);
  }
  .face:nth-of-type(3) {
    background: rgba(210, 207, 0, 0.6);
    transform: rotateY(90deg) translateZ(50px);
  }
  .face:nth-of-type(4) {
    background: rgba(116, 0, 210, 0.6);
    transform: rotateY(-90deg) translateZ(50px);
  }
  .face:nth-of-type(5) {
    background: rgba(210, 95, 0, 0.6);
    transform: rotateX(90deg) translateZ(50px);
  }
  .face:nth-of-type(6) {
    background: rgba(210, 0, 70, 0.6);
    transform: rotateX(-90deg) translateZ(50px);
  }
</style>

呈现效果：

translate 位移

translate 位移变换，使用 长度单位 设置移动距离。虽然名称叫位移，但元素的自身占用的位置还是存在的，变换后的位置也不会占用文档流。

语法：

transform: translate(tx, ty); /* 设置 2D 位移 */
transform: translate3d(tx, ty, tz); /* 设置 3D 位移 */
transform: translateX(tx); /* 设置 X 轴位移 */
transform: translateY(ty); /* 设置 Y 轴位移 */
transform: translateZ(tz); /* 设置 Z 轴位移 */

使用方式：

注意了本示例给一个盒子添加了多个 transform，仅为了演示使用方式，实际开发中只会生效一个 transform 属性：

.box {
  transform: translate(20px, 20px);
  transform: translate3d(20px, -20px, 200px);
  transform: translateX(20px);
  transform: translateY(20px);
  transform: translateZ(200px);
}

呈现效果：

CSS 的 3D 坐标系 Z 轴都是垂直于屏幕，所以 X 轴上的位移，会呈现近大远小的效果。

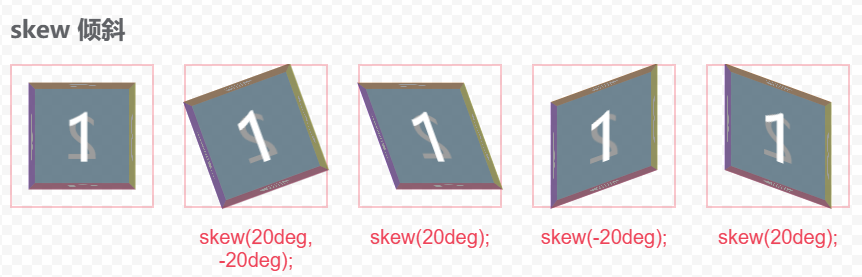
skew 倾斜

skew 可以让元素扭成一个平行四边形一样，使用 角度值 设置倾斜角度。

语法：

transform: skew(ax, ay); /* 设置 2D 倾斜*/
transform: skewX(ax); /* 设置水平方向倾斜*/
transform: skewY(ay); /* 设置垂直方向倾斜*/

使用方式：

.box {
  transform: skew(20deg, -20deg);
  transform: skewX(20deg);
  transform: skewY(-20deg);
  transform: skew(20deg);
}

呈现效果：

scale 缩放

元素的默认缩放倍率是 1，就是不进行任何缩放，小于 1 表所缩小倍数，大于 1 表示放大倍数，使用 倍率值 设置缩放倍率。

语法：

transform: scale(sx, sy);  /* 设置 2D 缩放 */
transform: scale3d(sx, sy, sz);  /* 设置 3D 缩放 */
transform: scaleX(sx);  /* 设置 3D X 轴缩放 */
transform: scaleY(sy);  /* 设置 3D Y 轴缩放 */
transform: scaleZ(sz);  /* 设置 3D Z 轴缩放 */

使用方式：

.box {
  transform: scale(1.1, 1.1);
  transform: scale3d(1.2, 1.2, 1.2);
  transform: scaleX(0.8);
  transform: scaleY(0.8);
  transform: scaleZ(2);
}

呈现效果：

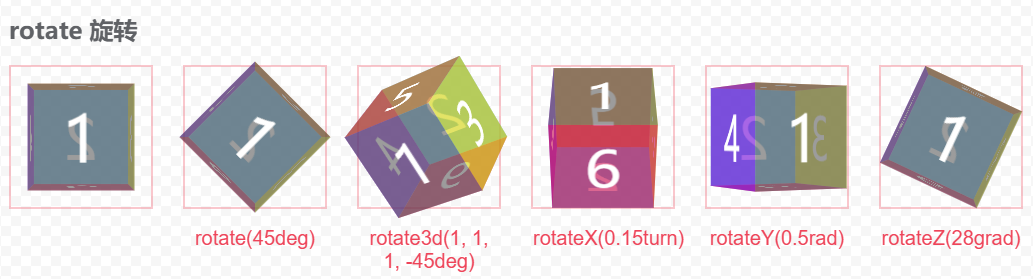
rotate 旋转

rotate 可以让元素旋转起来，使用 角度值 设置旋转角度，角度单位支持：

• deg 度数
• rad 弧度
• grad 梯度
• turn 圈数

一般就 deg 和 turn 比较常用。

语法：

transform: rotate(a);  /* 设置 2D 旋转角度 */
transform: rotate3d(x, y, z, a);  /* 设置 3D 旋转角度 */
transform: rotateX(a);  /* 设置 3D X 轴旋转角度 */
transform: rotateY(a);  /* 设置 3D Y 轴旋转角度 */
transform: rotateZ(a);  /* 设置 3D Z 轴旋转角度 */

使用方式：

.box {
  transform: rotate(45deg);
  transform: rotate3d(1, 1, 1, -45deg);
  transform: rotateX(0.15turn);
  transform: rotateY(0.5rad);
  transform: rotateZ(28grad);
}

呈现效果：

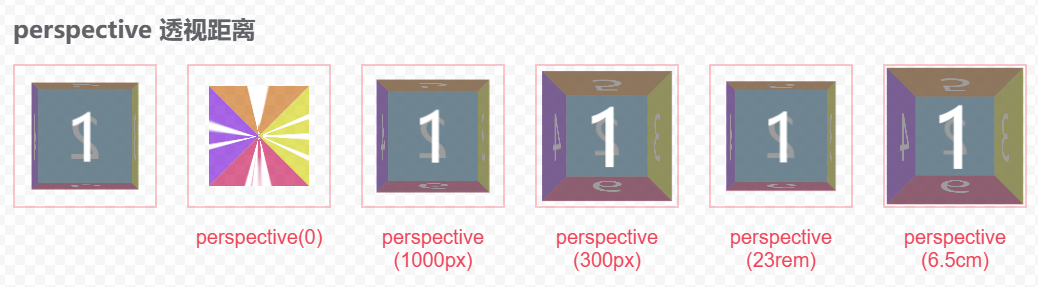
perspective 透视距离

perspective 设置 Z 轴的坐标原点（0）离观察者的距离，值越大会感觉越远，使用 距离单位。设置为 0 表示 Z 轴贴在了屏幕上，看起来就像无限大一样！！

语法：

transform: perspective(d);  /* 设置 3D 透视，值越大会感觉越远 */

使用方式：

.box {
  transform: perspective(0);
  transform: perspective(1000px);
  transform: perspective(300px);
  transform: perspective(143rem);
  transform: perspective(6.5cm);
}

呈现效果：

matrix 矩阵变换

矩阵变换是底层实现，旋转、缩放、移动、倾斜这些效果都是上层封装后的语法糖。

矩阵变换语法：

transform: matrix(a, b, c, d, tx, ty);  /* 2D 矩阵变换*/
transform: matrix3d(  /* 3D 矩阵变换，最底层的矩阵操作方法 */
  a1, b1, c1, d1, /* X轴的缩放和倾斜 */
  a2, b2, c2, d2, /* Y轴的缩放和倾斜 */
  a3, b3, c3, d3, /* Z轴的缩放和倾斜 */
  a4, b4, c4, d4  /* X、Y、Z轴位移，d4 常量是 1*/
);

/*
matrix(a, b, c, d, tx, ty)
是
matrix3d(
  a, b, 0, 0,
  c, d, 0, 0,
  0, 0, 1, 0,
  tx, ty, 0, 1
)
的简写。
*/

2D 矩阵变换

矩阵算法梦回大学，具体原理就不详解了，有兴趣可以看看线性代数相关书籍，具体算法：

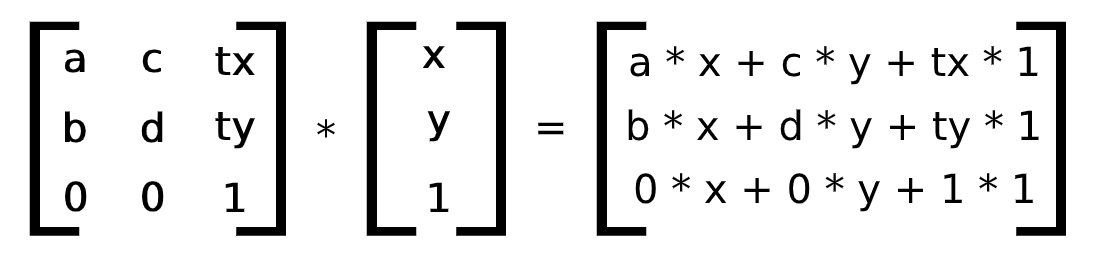
至于后面的 0 0 1 是什么，这个又跟 齐次坐标系 拉上关系了，有兴趣可参阅维基百科：https://zh.wikipedia.org/wiki/齐次坐标

其中的 x,y 表示的元素中的每个像素点的 x,y 坐标，计算的结果则是变化后的 x,y 坐标。

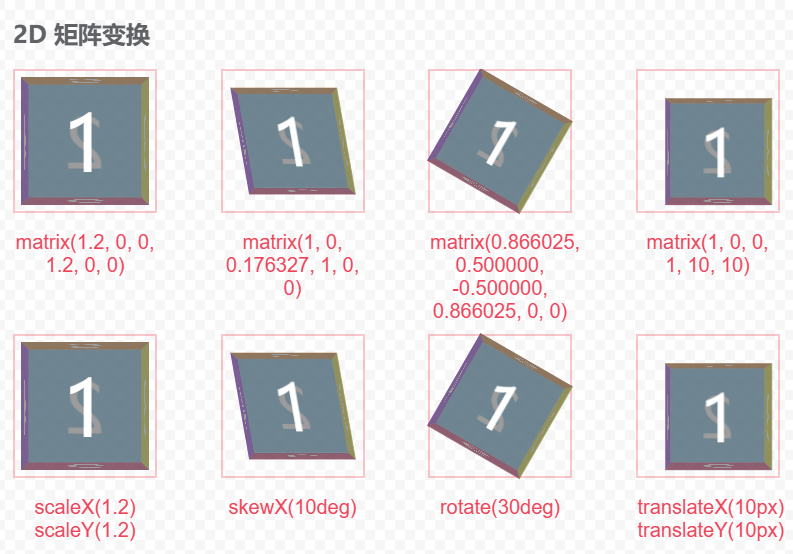
使用方式：

.box {
  transform: matrix(1.2, 0, 0, 1.2, 0, 0);
  /* 与 transform: scaleX(1.2) scaleY(1.2); 相同 */

  transform: matrix(1, 0, 0.176327, 1, 0, 0);
  /* 与 transform: skewX(10deg); 相同 */

  transform: matrix(0.866025, 0.500000, -0.500000, 0.866025, 0, 0);
  /* 与 transform: rotate(30deg); 相同 */

  transform: matrix(1, 0, 0, 1, 10, 10);
  /* 与 transform: translateX(10px) translateY(10px); 相同 */

}

呈现效果：

语法糖的换算规则：

变换类型	变换方法	matrix 写法
平移	translate(translateX, translateY)	matrix(1, 0, 0, 1, translateX, translateY)
缩放	scale(scaleX, scaleY)	matrix(scaleX, 0, 0, scaleY, 0, 0)
斜拉	skew(angleX, angleY)	matrix(1, tan(angleY), tan(angleX), 1, 0, 0)
旋转	rotate(angle)	matrix(cos(angle), sin(angle), -sin(angle), cos(angle), 0, 0)

3D 矩阵变换

2D 变换是 3*3 的矩阵，3D 则是 4*4 的矩阵，3D 比 2D 多出一个维度的空间，算法复杂度可不是 1+1 那么简单了。

3D 矩阵变换算法：

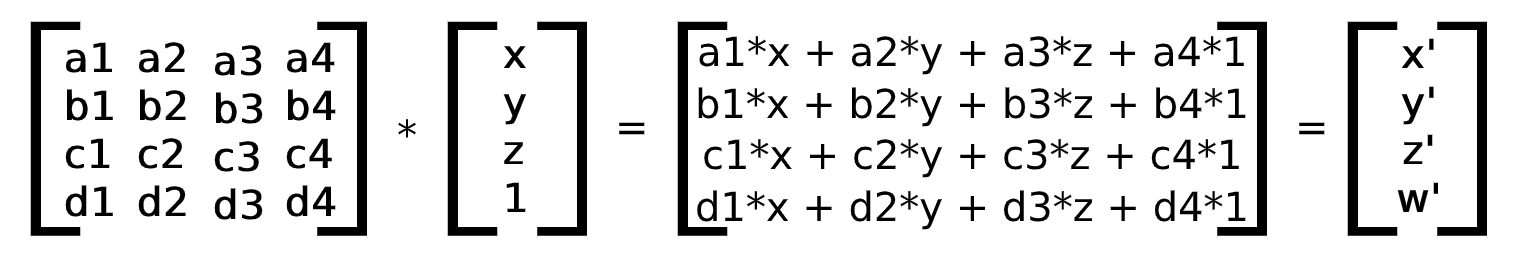
最终三维空间坐标：(x'/w', y'/w', z'/w')。

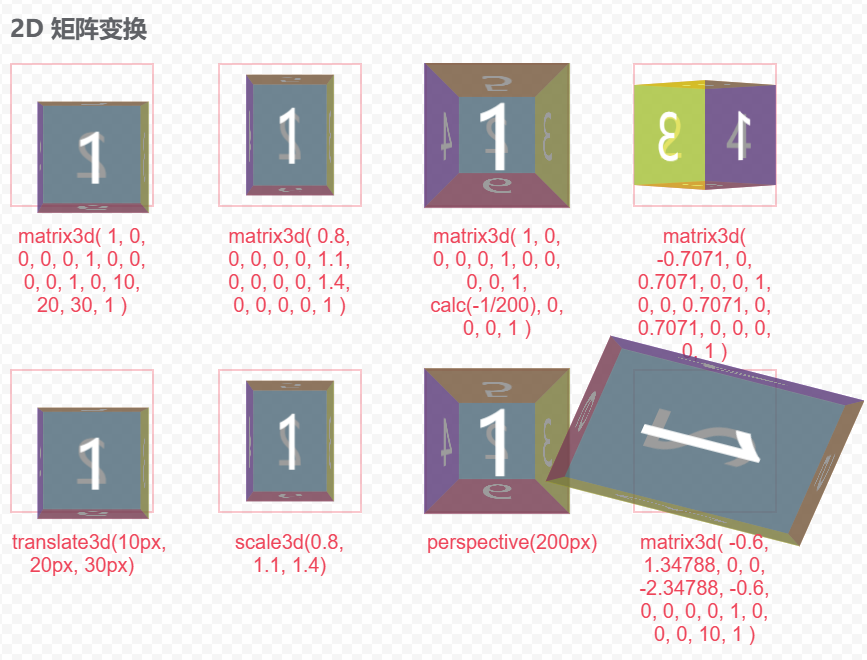
3D 平移使用矩阵表示方法：

transform: matrix3d(
  1, 0, 0, 0,
  0, 1, 0, 0,
  0, 0, 1, 0,
  translateX, translateY, translateZ, 1
);

3D 缩放使用矩阵表示方法：

transform: matrix3d(
  scaleX, 0, 0, 0,
  0, scaleY, 0, 0,
  0, 0, scaleZ, 0,
  0, 0, 0, 1
);

3D 倾斜使用矩阵表示方法：

transform: matrix3d(
  1, tan(θ_yx), tan(θ_zx), 0,
  tan(θ_xy), 1, tan(θ_zy), 0,
  tan(θ_xz), tan(θ_yz), 1, 0,
  0, 0, 0, 1
);

每个 tanθ 对应不同平面的倾斜角度。

旋转使用矩阵表示方法：

/* 绕 Z 轴旋转( */
transform: matrix3d(
  cos(angle), sin(angle), 0, 0,
  −sin(angle), cos(angle), 0, 0,
  0, 0, 1, -1/d,
  0, 0, 0, 1
);
/* 绕 X 轴旋转( */
transform: matrix3d(
  1, 0, 0, 0,
  0, cos(angle), sin(angle), 0,
  0, −sin(angle), cos(angle), 0,
  0, 0, 0, 1
);
/* 绕 Y 轴旋转( */
transform: matrix3d(
  cos(angle), 0, −sin(angle), 0,
  0, 1, 0, 0,
  sin(angle), 0, cos(angle), 0,
  0, 0, 0, 1
);

透视使用矩阵表示方法：

transform: matrix3d(
  1, 0, 0, 0,
  0, 1, 0, 0,
  0, 0, 1, -1/d,
  0, 0, 0, 1
);

呈现效果：

与 transform 相关的属性

属性	作用	典型值
transform	应用变换	rotate(45deg) translateX(20px)
transform-origin	设置变换原点	left top, 50% 100%
transform-style	保留子元素 3D 空间	preserve-3d
perspective	定义 3D 观察深度	1000px
perspective-origin	设置观察者视角位置	20% 80%
backface-visibility	控制背面可见性	hidden

这些属性用于设置与 transform 相关的效果，比如设置变换原点，是否应用 3D 空间，设置透视视角等，这里就不再一一演示，有兴趣可自行写一下例子看看效果。

总结

transform 提供的基础变换已足以满足日常需求，一些特殊的变化有可能会用上矩阵，不过这么多年的前端经验来看，能用上矩阵的场景几乎不可见。

由于 transform 不改变文档流的特性，所以在 CSS 动画中，此属性应用非常广泛。

参考资料

https://developer.mozilla.org/zh-CN/docs/Web/CSS/transform-function/matrix

https://www.zhangxinxu.com/wordpress/2012/06/css3-transform-matrix-矩阵/

https://www.cnblogs.com/cjc-0313/p/16472278.html