Standard Error of Mean(s.e.m.)

· 来源：http://www.dxy.cn/bbs/thread/6492633#6492633

6楼：

“据我所知，SD( standard deviation )反应的是观测值的变异性，其表示平均数的代表性，而SEM是 standard error of mean, 是平均数的抽样误差，反应平均数的抽样准确性，由于真实值是不知道的，统计估计值的准确性无法度量，但利用统计学方法可以度量精确性。试验的误差来源有系统误差和抽样误差（随机误差），系统误差易于克服，抽样误差由许多无法控制的内因和外因，带有偶然性，在试验中即使十分小心也难以消除，但可以通过增加重复数来来降低。 对于重复数少的小样本（n≤30）用mean ± S.E.M.，重复数多的大样本（n＞30）用 mean ± SD。”

· WIKI: https://en.wikipedia.org/wiki/Standard_error

The standard error of the mean (SEM) is the standard deviation of the sample-mean's estimate of a population mean. (It can also be viewed as the standard deviation of the error in the sample mean with respect to the true mean, since the sample mean is an unbiased estimator.) SEM is usually estimated by the sample estimate of the population standard deviation (sample standard deviation) divided by the square root of the sample size (assuming statistical independence of the values in the sample):

where

s is the sample standard deviation (i.e., the sample-based estimate of the standard deviation of the population), and

n is the size (number of observations) of the sample.

· 区分“standard deviation”（标准差）和“standard errer”（标准误（差））

标准差：衡量一组数的离散程度，标准误：样本统计量的标准差，是衡量样本抽样的误差的指标。

来源：http://www.zhihu.com/question/21925923

standard deviation是标准差 表示一组数值之间的离散程度
计算公式：

<span style="font-family: Microsoft YaHei; font-size: 18px;"><span style="font-size: 18px;" data-mce-style="font-size: 18px;"><span style="font-size: 18px;" data-mce-style="font-size: 18px;"><img src="http://pic1.zhimg.com/0958793376d47c9361d4a9b0854353c4_b.jpg" data-rawwidth="234" data-rawheight="87" class="content_image" width="234"></span></span></span>

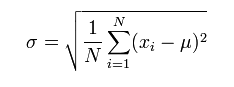
简单来说就是一组数据的每一个数与该组数据的平均值比较，通过得出来的数值看这组数据的离散程度。比如，全班男同学身高都差不多是1.75m，那么我们可以说这个班的男生身高标准差很小，因为大家都接近平均值就是说数据很集中。可是，五个姚明，十个潘长江组成一组，嗯，这个身高数据很离散，参差不齐，标准差很大....

standard error 是标准误 是样本统计量的标准差
在现实中，我们无法得知总体情况，总是以样本的分布情况去推断总体。比如，我国在校大学生每月伙食费用是多少。对于这个问题，我们不能全国范围统计各大高校每个同学的伙食费，于是，我们就用样本推断总体大概情况以得出我们所需要的数据。比如，抽取我国都东西南北部分高校部分同学的伙食费进行研究。而此时，标准误产生了。它是衡量样本抽样的误差的指标。

再举一个例子说清楚问题。
比如总体是1 2 3 4 5 6 7 8 9 10 总体平均数是：5.5
而甲对总体进行抽样，可能得到 5 8 3 2 平均数是4.5
乙进行抽样，得到 3 7 9 2 平均数5.25
丙抽样，得到 4 6 9 2 4 1 平均数为4.3
丁...............................平均数为x
那么，4.5， 5.25 ，4.3.........x 组成一个新分布，这是一个以样本平均数为分布的，那么这个分布的标准差是什么呢？利用公式，我们可以得出这个分布的标准差，而这个标准差就是标准误。（当然这个分布的统计量有平均数，标准差，方差，相关系数等等。而我们这里以平均数为栗子。）

如果知道总体的标准差，
如果，不知道总体的标准差，用样本的标准差，采用它的无偏估计
简单说就是统计量（样本）的标准差。

· 来源： http://blog.sciencenet.cn/blog-479412-481776.html

标准差表示数据的离散程度，或者说数据的波动大小。标准误表示抽样误差的大小。

统计教材上一般都写标准误表示均数的抽样误差，这对于初学者很难理解。这里通过举例来说明含义。

比如，有一个学校，学校中共有1000名学生，则这1000名学生可以作为这个学校学生的总体。如果我想了解所有学生的身高，采用随机抽样，抽取了50人。这50人就是一个样本。这里需要注意：一个样本并不是指一个人，而是指一次抽样。一个样本可以是1个人，也可以是100人，这里的1和100就是样本大小。

从理论上讲，抽样误差表示这样的意思：即如果不止抽样一次，而是抽样10次，每次都50人，那么我就有10个均数和标准差。总体1000人，一个样本，即50人。每个样本都能计算计算一个均数和标准差。

以这10个均数作为原始数据，仍然能计算出一个均数和标准差，以这10个均数计算出的标准差就称之为标准误。这是理论上的含义，实际的含义就代表抽样误差的大小，即抽取的样本代表性好不好，抽样误差越小，代表性越好，反之，代表性越差。

如果我对学校中的1000人都测量了身高，那理论上就没有标准误，也就是没有抽样误差了，因为我测量了总体，这时就不存在标准误了。但是标准差是存在的，因为这1000人的身高肯定不同，肯定会有波动。这里就充分表明了标准差和标准误的区别了。

标准差与标准误的意义、作用和使用范围均不同。标准差(亦称单数标准差）一般用s 表示,是表示个体间变异大小的指标,反映了整个样本对样本平均数的离散程度,是数据精密度的衡量指标;而标准误一般用S_x 表示,反映样本平均数对总体平均数的变异程度,从而反映抽样误差的大小,是量度结果精密度的指标。

样本标准差：

样本平均数的标准误：

 

回复2楼：

两者的区别可以这样表述：标准差是某个样本数据方差的平方根，它衡量的是该样本数据的离散程度；标准误是在多次抽样中样本均值的标准差，衡量的是样本均值的离散程度。而在实际的抽样中，习惯用样本均值来推断总体均值，那么样本均值的离散程度（标准误）越大，抽样误差就越大，应此可以用标准误来衡量抽样误差的大小。
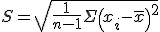
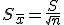
在实际的应用中，标准差主要有两点作用，一是用来对样本进行标准化处理，即样本观察值减去样本均值，然后除以标准差，这样就变成了标准正态分布；二是通过标准差来确定异常值，常用的方法就是样本均值加减n倍的标准差。标准误的作用主要是用来做区间估计，常用的估计区间是均值加减n倍的标准误。