HDU 4802 && HDU 4803 贪心,高精 && HDU 4804 轮廓线dp && HDU 4805 计算几何 && HDU 4811 (13南京区域赛现场赛 题目重演A,B,C,D,J)
A.GPA(HDU4802):
给你一些字符串对应的权重,求加权平均,如果是N,P不计入统计
GPA
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1193 Accepted Submission(s): 743
The GPA is the weighted average score of all courses one student may take, if we treat the credit as the weight. In other words,
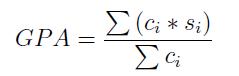
An additional treatment is taken for special cases. Some courses are based on “Pass/Not pass” policy, where stude nts earn a mark “P” for “Pass” and a mark “N” for “Not pass”. Such courses are not supposed to be considered in computation. These special courses must be ignored for computing the correct GPA.
Specially, if a student’s credit in GPA computation is 0, his/her GPA will be “0.00”.
Each test case starts with a line containing one integer N (1 <= N <= 1000), the number of courses. Then follows N lines, each consisting the credit and the mark of one course. Credit is a positive integer and less than 10.
2 B
3 D-
2 P
1 F
3 A
2
2 P
2 N
6
4 A
3 A
3 A
4 A
3 A
3 A
0.00
4.00
For the first test case:
GPA =(3.0 * 2 + 1.0 * 3 + 0.0 * 1 + 4.0 * 3)/(2 + 3 + 1 + 3) = 2.33
For the second test case: because credit in GPA computation is 0(P/N in additional treatment), so his/her GPA is “0.00”.
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<cmath>
#include<cstring> using namespace std; int main()
{
int n,nn,num;
double res,mid;
char cc[];
while(scanf("%d",&n)!=EOF){
res=;
num=;
for(int k=;k<n;k++){
mid=;
scanf("%d%s",&nn,cc);
if(cc[]=='P'||cc[]=='N') continue;
if(cc[]=='A'){
if(cc[]=='\0') mid+=4.0;
else if(cc[]=='-') mid+=3.7;
}
else if(cc[]=='B'){
if(cc[]=='\0') mid+=3.0;
else if(cc[]=='+') mid+=3.3;
else if(cc[]=='-') mid+=2.7;
}
else if(cc[]=='C'){
if(cc[]=='\0') mid+=2.0;
else if(cc[]=='+') mid+=2.3;
else if(cc[]=='-') mid+=1.7;
}
else if(cc[]=='D'){
if(cc[]=='\0') mid+=1.3;
else if(cc[]=='-') mid+=1.0;
}
num+=nn;
res+=mid*nn;
}
if(num==) printf("0.00\n");
else printf("%.2f\n",res/num);
}
return ;
}
B.Poor Warehouse Keeper(HDU4803)
Poor Warehouse Keeper
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1089 Accepted Submission(s): 312
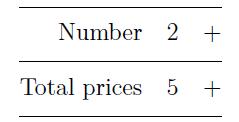
There are only two buttons on the screen. Pressing the button in the first line once increases the number on the first line by 1. The cost per unit remains untouched. For the screen above, after the button in the first line is pressed, the screen will be:
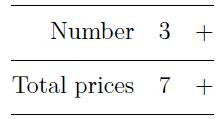
The exact total price is 7.5, but on the screen, only the integral part 7 is shown.
Pressing the button in the second line once increases the number on the second line by 1. The number in the first line remains untouched. For the screen above, after the button in the second line is pressed, the screen will be:
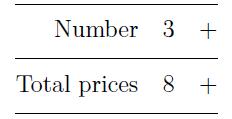
Remember the exact total price is 8.5, but on the screen, only the integral part 8 is shown.
A new record will be like the following:
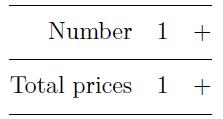
At that moment, the total price is exact 1.0.
Jenny expects a final screen in form of:
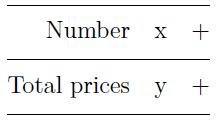
Where x and y are previously given.
What’s the minimal number of pressing of buttons Jenny needs to achieve his goal?
Each test case contains one line with two integers x(1 <= x <= 10) and y(1 <= y <= 109) separated by a single space - the expected number shown on the screen in the end.
3 8
9 31
5
11
For the second test case, one way to achieve is:
(1, 1) -> (1, 2) -> (2, 4) -> (2, 5) -> (3, 7.5) -> (3, 8.5)
题意:有个电子屏 上x,下y,上下各有按钮,上面的按钮保持分子分母比例使x+1,(也即x/y=(x+1)/(y+deltay)),下面的直接y+1,小数不显示但是不约去
赛时总结:打乱了smilewsw的节奏.....这题没做出来有三点
2. 应该稍微比下界少一点就行了,这里的一点不是deltay为整数的时候就直接-1
3. double的运算应该放到一起去,不能先得到(y+deltay)换算成整数后再减去y,而是应该在得到整数前减去y,忽略了y可能是个小数这一点
解题思路:贪心,肯定应该介于x/(y+1),x/(y-1)之间,又因为比例越小,那么按上面的键y增的越多,所以不用管x/(y-1),尽量逼近但是又不超过x/(y+1)即可,所以设下限为x/(y+1-eps),
贪心证明在于这个比例只能被扩大不能缩小
#include<cstdio>
using namespace std;
int x,y;
int main()
{
while(scanf("%d%d",&x,&y)==2){
if(x>y){puts("-1");continue;}
if(x==1||x==y){printf("%d\n",y-1);continue;}
double sub,dow;
sub=x;
dow=y+1-0.01; double ty=1;//用来放置过程中的y,过程中的x为i
int ans=x-1;//肯定要增减x-1次,用于上方的键
for(int i=1;i<=x;i++){
int deltay=(int)((i*dow)/sub-ty);//按下方键的次数
ans+=deltay;
ty+=deltay;
ty=ty*(i+1)/i;//按了上方的键
}
printf("%d\n",ans);
}
return 0;
}
C. Campus Design(HDU4804):
Campus Design
Time Limit: 15000/8000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 406 Accepted Submission(s): 201
The designers measured the open space and come to a conclusion that the open space is a rectangle with a length of n meters and a width of m meters. Then they split the open space into n x m squares. To make it more beautiful, the designer decides to cover the open space with 1 x 1 bricks and 1 x 2 bricks, according to the following rules:
1. All the bricks can be placed horizontally or vertically
2. The vertexes of the bricks should be placed on integer lattice points
3. The number of 1 x 1 bricks shouldn’t be less than C or more than D. The number of 1 x 2 bricks is unlimited.
4. Some squares have a flowerbed on it, so it should not be covered by any brick. (We use 0 to represent a square with flowerbet and 1 to represent other squares)
Now the designers want to know how many ways are there to cover the open space, meeting the above requirements.
Each test case starts with a line containing four integers N(1 <= N <= 100), M(1 <= M <= 10), C, D(1 <= C <= D <= 20). Then following N lines, each being a string with the length of M. The string consists of ‘0’ and ‘1’ only, where ‘0’ means the square should not be covered by any brick, and ‘1’ otherwise.
1
1 1 1 2
0
1 1 1 2
1
1 2 1 2
11
1 2 0 2
01
1 2 0 2
11
2 2 0 0
10
10
2 2 0 0
01
10
2 2 0 0
11
11
4 5 3 5
11111
11011
10101
11111
0
1
1
1
2
1
0
2
954
题意:轮廓线DP
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<cmath>
#include<cstring>
#define MOD 1000000007
using namespace std;
long long dp[2][1<<11][21];
char a[200][50];
int main()
{
int n,m,c,d,i,j,used,k,cnt;
while(scanf("%d %d %d %d",&n,&m,&c,&d)!=EOF)
{
memset(dp,0,sizeof(dp));
for(i=0;i<n;i++)
scanf("%s",a[i]);
dp[0][0][0]=1;
cnt=0;
for(i=0;i<n;i++)
{
for(j=0;j<m;j++)
{
memset(dp[1-cnt%2],0,sizeof(dp[1-cnt%2]));
for(used=0;used<1<<m;used++)
{
for(k=0;k<=d;k++)
{
if((used>>j&1)||a[i][j]=='0')
dp[1-cnt%2][used&~(1<<j)][k]=(dp[1-cnt%2][used&~(1<<j)][k]+dp[cnt%2][used][k])%MOD;
else
{
if(k<d)
dp[1-cnt%2][used&~(1<<j)][k+1]=(dp[1-cnt%2][used&~(1<<j)][k+1]+dp[cnt%2][used][k])%MOD;
if(j+1<m&&!(used>>(j+1)&1)&&a[i][j+1]=='1')
dp[1-cnt%2][used|1<<(j+1)][k]=(dp[1-cnt%2][used|1<<(j+1)][k]+dp[cnt%2][used][k])%MOD;
if(i+1<n&&a[i+1][j]=='1')
dp[1-cnt%2][used|1<<j][k]=(dp[1-cnt%2][used|1<<j][k]+dp[cnt%2][used][k])%MOD;
}
}
}
cnt++;
}
}
long long sum=0;
for(i=c;i<=d;i++)
{
sum=(sum+dp[cnt%2][0][i])%MOD;
}
printf("%I64d\n",sum);
}
return 0;
}
D. Shoot(HDU4805):
Shoot
Time Limit: 30000/15000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 315 Accepted Submission(s): 50
Special Judge
Levi was born with the remarkable ability of counter-surveillance, it was just a piece of cake for him to reach Evil Army’s power bases. Each power base can be represented as a triangle in 3D-Cartesian coordinate system. The only weapon Levi had was a laser cannon which can shoot in both two directions simultaneously. To avoid being caught by enemy, Levi can only place the laser cannon somewhere on a segment from S to T. Unfortunately, there was something wrong with the laser cannon, Levi can’t adjust its shooting angle, so the shooting direction was fixed.
Since Levi didn’t have any time to find the best place to shoot the laser, he decided to select a point on the segment randomly to place the cannon. If the laser touched the base(even the boundary), the base will be destroyed. Your task is to calculate the expected number of the destroyed bases in just one shoot.
It is recommended to see the sample input to understand the problem statement more clearly.
For each test case, the first line is an integer N (1 <= N <= 100000), the number of enemy’s power bases. Each of the next three lines contains 3 integers, x, y, z, denoting the coordinates of S, T, and the fixed shooting direction. The last N lines contains 9 integers, x1, y1, z1, x2, y2, z2, x3, y3, z3, denoting the coordinates of the three vertices of enemy’s power base. It is guaranteed that all the triangles will not degenerate.
And the absolute value of all numbers except N and T will not exceed 1000.
Any answer within an absolute error less than or equal to 10-6 would be accepted.
0 0 0
2 0 0
0 0 1
-1 0 1 1 0 1 -1 0 2
1 1 -1 1 -1 -1 2 0 -1
#include <map>
#include <set>
#include <list>
#include <cmath>
#include <ctime>
#include <deque>
#include <queue>
#include <stack>
#include <bitset>
#include <cctype>
#include <cstdio>
#include <string>
#include <vector>
#include <cassert>
#include <cstdlib>
#include <cstring>
#include <iomanip>
#include <sstream>
#include <iostream>
#include <algorithm> using namespace std; #define PB push_back
#define MP make_pair
#define AA first
#define BB second
#define OP begin()
#define ED end()
#define SZ size()
#define SORT(x) sort(x.OP,x.ED)
#define SQ(x) ((x)*(x))
#define SSP system("pause")
#define cmin(x,y) x=min(x,y)
#define cmax(x,y) x=max(x,y)
typedef long long LL;
typedef pair<int, int> PII;
const double eps=1e-8;
const double PI=acos(-1.);
const LL MOD = 1000000007;
int sign(double x) {return x<-eps?-1:x>eps;}
struct spt {
double x,y,z;
spt(double _x=0,double _y=0,double _z=0) :x(_x),y(_y),z(_z) {}
spt operator + (spt s) {return spt(x+s.x,y+s.y,z+s.z);}
spt operator - (spt s) {return spt(x-s.x,y-s.y,z-s.z);}
spt operator * (double s) {return spt(x*s,y*s,z*s);}
spt operator / (double s) {return spt(x/s,y/s,z/s);}
double len() const {return sqrt(SQ(x)+SQ(y)+SQ(z));}
double operator * (spt s) {return x*s.x+y*s.y+z*s.z;} //点积dot
spt operator ^ (spt s) { //叉积det
spt ret;
ret.x=y*s.z-z*s.y;
ret.y=z*s.x-x*s.z;
ret.z=x*s.y-y*s.x;
return ret;
}
void output(char *s="") {printf("%s:%.6f %.6f %.6f\n",s,x,y,z);}
void input() {scanf("%lf%lf%lf",&x,&y,&z);}
} Orz(0,0,0);
spt S,T,V,A,B,C;
double disLP(spt p1,spt p2,spt q) {
return fabs((p2-p1)*(q-p1)/(p2-p1).len());
}
double disLL(spt p1,spt p2,spt q1,spt q2) {
spt p=q1-p1,u=p2-p1,v=q2-q1;
double d=(u*u)*(v*v)-SQ(u*v);
if(sign(d)==0)return disLP(q1,q2,p1);
double s=((p*u)*(v*v)-(p*v)*(u*v))/d;
return disLP(q1,q2,p1+u*s);
}
int isFL(spt p,spt o,spt q1,spt q2,spt &is) {
double a=o*(q2-p),b=o*(q1-p);
double d=a-b;
if(sign(d)==0)return 0;
is=(q1*a-q2*b)/d;
return 1;
}
int isFF(spt p1,spt o1,spt p2,spt o2,spt &ip,spt &io) {
spt e=o1^o2;
spt v=o1^e;
double d=o2*v;
if(sign(d)==0)return 0;
ip=p1+v*(o2*(p2-p1))/d,io=e;
return 1;
}
int inner(spt O,spt A,spt B,spt C) {
double S=((B-A)^(C-A)).len();
double S1=((A-O)^(B-O)).len();
double S2=((A-O)^(C-O)).len();
double S3=((C-O)^(B-O)).len();
return sign(S-S1-S2-S3)==0;
}
int inner(double o,double a,double b) {
return sign(max(a,b)-o)>=0&&sign(min(a,b)-o)<=0;
}
int inner(spt O,spt A,spt B) {
return inner(O.x,A.x,B.x)&&inner(O.y,A.y,B.y)&&inner(O.z,A.z,B.z);
}
int main() {
//freopen("","r",stdin);
//freopen("","w",stdout);
int i,j,k,u,v,w,p,q,r,n,m;
while(~scanf("%d",&n)) {
S.input(),T.input();
V.input();
double ans=0;
spt U= (S-T) ^V;
for(j=0; j<n; j++) {
A.input(),B.input(),C.input();
spt D= (B-A) ^ (C-A);
if(sign(D.len()) ==0) continue;
if(sign(U.len())==0) {
//TODO S->T Yu V PingXing
spt is;
int f=isFL(A,D,S,S+V,is);
if(f) {
ans+=inner(is,A,B,C);
continue;
}
if(sign((S-A)*D))continue;
spt iAB,iBC,iAC;
int fAB=isFL(A,D^(A-B),S,S+V,iAB);
int fBC=isFL(B,D^(B-C),S,S+V,iBC);
int fAC=isFL(C,D^(C-A),S,S+V,iAC);
fAB&=inner(iAB,A,B);
fBC&=inner(iBC,B,C);
fAC&=inner(iAC,A,C);
ans+=fAB|fBC|fAC;
continue;
}
if(sign(V*D)==0) {
if(sign((S-A)*D)==0&&sign((T-A)*D)==0) {
//TODO V//ABC && STABC on flat
spt iA,iB,iC;
int fA=isFL(S,(T-S)^D,A,A+V,iA);
int fB=isFL(S,(T-S)^D,B,B+V,iB);
int fC=isFL(S,(T-S)^D,C,C+V,iC);
double len=(T-S).len();
double le=0,re=len;
vector<double>L;
if(fA)L.PB((iA-S)*(T-S)/len);
if(fB)L.PB((iB-S)*(T-S)/len);
if(fC)L.PB((iC-S)*(T-S)/len);
sort(L.OP,L.ED);
if(L.SZ<2)continue;
double pe=L[0],qe=L[L.SZ-1];
cmax(pe,le);
cmin(qe,re);
if(qe>pe)ans+=(qe-pe)/len;
}
continue;
}
spt SP,TP,iAB,iBC,iAC;
assert(isFL(A,D,S,S+V,SP));
assert(isFL(A,D,T,T+V,TP));
if(inner(SP,A,B,C)&&inner(TP,A,B,C)) {ans+=1; continue;}
vector<spt>L;
L.PB(SP),L.PB(TP);
int fAB=isFL(A,D^(A-B),SP,TP,iAB);
int fBC=isFL(B,D^(B-C),SP,TP,iBC);
int fAC=isFL(C,D^(C-A),SP,TP,iAC);
double len=(SP-TP).len();
if(fAB&&inner(iAB,SP,TP))for(i=0; i+1<L.SZ; i++)
if(inner(iAB,L[i],L[i+1])) {L.insert(L.OP+i+1,iAB); break;}
if(fBC&&inner(iBC,SP,TP))for(i=0; i+1<L.SZ; i++)
if(inner(iBC,L[i],L[i+1])) {L.insert(L.OP+i+1,iBC); break;}
if(fAC&&inner(iAC,SP,TP))for(i=0; i+1<L.SZ; i++)
if(inner(iAC,L[i],L[i+1])) {L.insert(L.OP+i+1,iAC); break;}
for(i=0; i+1<L.SZ; i++) {
spt mid=(L[i]+L[i+1])/2;
if(inner(mid,A,B,C))
ans+=(L[i+1]-L[i]).len()/len;
}
}
printf("%.8f\n",ans);
}
return 0;
}
J:水题
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<cmath>
#include<cstring> using namespace std;
long long a[];
int main()
{
while(scanf("%I64d%I64d%I64d",a,a+,a+)==){
sort(a,a+);
if(a[]==&&a[]==){
printf("%I64d\n",*a[]-<?:*a[]-);
}
else if(a[]==&&a[]==){
printf("%I64d\n",*a[]->?*a[]-:);
}
else if(a[]==&&a[]==){
printf("%I64d\n",a[]==?:*a[]-);
}
else if(a[]==){
printf("%I64d\n",*a[]+*a[]-);
}
else if(a[]==){
printf("%I64d\n",*a[]+*a[]-);
}
else {
printf("%I64d\n",*a[]+*a[]+*a[]-);
}
}
return ;
}
HDU 4802 && HDU 4803 贪心,高精 && HDU 4804 轮廓线dp && HDU 4805 计算几何 && HDU 4811 (13南京区域赛现场赛 题目重演A,B,C,D,J)的更多相关文章
- [贪心][高精]P1080 国王游戏(整合)
题目描述 恰逢 H 国国庆,国王邀请 n 位大臣来玩一个有奖游戏.首先,他让每个大臣在左.右手上面分别写下一个整数,国王自己也在左.右手上各写一个整数.然后,让这 n 位大臣排成一排,国王站在队伍的最 ...
- 国王游戏 2012年NOIP全国联赛提高组(贪心+高精)
P1080 国王游戏 题目描述 恰逢 H 国国庆,国王邀请 n 位大臣来玩一个有奖游戏.首先,他让每个大臣在左.右手上面分别写下一个整数,国王自己也在左.右手上各写一个整数.然后,让这 n 位大臣排成 ...
- noip 2012 国王游戏（贪心+高精）
/* 我是不会说我考试的时候想到了正解却把金币取大看成金币求和的.... 觉得只按左右手乘积排序不太对 有反例 也可能我反例放到这个题里是错的吧 按自己的理解排的序 就是各种讨论... 假设 第i个人 ...
- NOIP 2012 T2 国王游戏 （贪心+高精）
思路: 呃呃网上那么多题解写得都不错-.. 就是高精 巨坑... 这里展出的是任氏高精(纯自己yy滴) //By SiriusRen #include <cstdio> #include ...
- HDU - 5686-Problem B (递推+高精）
度熊面前有一个全是由1构成的字符串,被称为全1序列.你可以合并任意相邻的两个1,从而形成一个新的序列.对于给定的一个全1序列,请计算根据以上方法,可以构成多少种不同的序列. Input 这里包括多组测 ...
- HDU 5122 K.Bro Sorting（2014北京区域赛现场赛K题 模拟）
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=5122 解题报告:定义一种排序算法,每一轮可以随机找一个数,把这个数与后面的比这个数小的交换,一直往后判 ...
- HDU 4793 Collision(2013长沙区域赛现场赛C题)
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=4793 解题报告:在一个平面上有一个圆形medal,半径为Rm,圆心为(0,0),同时有一个圆形范围圆心 ...
- HDU 4791 Alice's Print Service(2013长沙区域赛现场赛A题)
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=4791 解题报告:打印店提供打印纸张服务,需要收取费用,输入格式是s1 p1 s2 p2 s3 p3.. ...
- HDU 5119 Happy Matt Friends（2014北京区域赛现场赛H题 裸背包DP）
虽然是一道还是算简单的DP,甚至不用滚动数组也能AC,数据量不算很大. 对于N个数,每个数只存在两个状态,取 和 不取. 容易得出状态转移方程: dp[i][j] = dp[i - 1][j ^ a[ ...
随机推荐
- Linux驱动模块的Makefile分析【转】
本文转载自:http://blog.chinaunix.net/uid-29307109-id-3993784.html 1． 获取内核版本 当设备驱动需要同时支持不同版本内核时,在编译阶段,内核模块 ...
- ubuntu下桌面假死处理方法(非重启)
一.背景 2018/05/22,就在这一天,进入ubuntu的桌面后随便点击任何位置均无法响应,此时又不想重启,遂出此文 二.解决方案 2.1 关掉Xorg进程 2.1.1按下ctrl+alt+F1进 ...
- winform中splitter的用法
1.将winform分为三列 整个窗体分成可以自动调节的三列的做法:1.往窗体上丢两个panel控件其中:panelLeft——设置Dock属性为“left”,并调节好其宽度panelRight——设 ...
- dp问题 -挑战例题 2017-7-24
01 背包 题意: 在N件物品取出若干件放在容量为W的背包里,每件物品的体积为W1,W2……Wn(Wi为整数),与之相对应的价值为P1,P2……Pn(Pi为整数).求背包能够容纳的最大价值. f[i] ...
- 论文笔记——SQUEEZENET ALEXNET-LEVEL ACCURACY WITH 50X FEWER PARAMETERS AND <0.5MB MODEL SIZE
论文地址:https://arxiv.org/abs/1602.07360 模型地址:https://github.com/DeepScale/SqueezeNet 1. 论文思想 提出一种新的卷积组 ...
- 论文笔记——PRUNING FILTERS FOR EFFICIENT CONVNETS
论文地址:https://arxiv.org/abs/1608.08710 主要思想 这篇文章主要讲了对filters的裁剪,裁剪方法是计算L1范数,然后裁剪掉较少的,多少取决于加速比. 实现效果 V ...
- 操作构造字符串化宏#define STRINGIZE(x) #x
c++test工程单元测试中报错 “STRINGIZE” 未定义错误 解决方案:在头文件定义宏STRINGIZE #符号把一个符号直接转换为字符串,例如:#define STRINGIZE(x) #x ...
- Intel微处理器学习笔记（三） 不可见寄存器
参考资料: 1. http://blog.chinaunix.net/uid-20797642-id-2495244.html 2. http://www.techbulo.com/708.htm ...
- [原][JSBSim]基于qt代码实现：TCP|UDP与飞行模拟软件JSBSim的通信，现实模型飞行！
废话没有,上关键代码 头文件 #include <QUdpSocket> #include <qtcpsocket.h> #ifndef vrUDP #define vrUDP ...
- shuoj 418 丢史蒂芬妮（素数筛+sg函数）
丢史蒂芬妮 代码: #include<bits/stdc++.h> using namespace std; +; int SG[N][N]; bool S[N]; vector<i ...