八大排序算法python实现

一、概述

 

排序有内部排序和外部排序，内部排序是数据记录在内存中进行排序，而外部排序是因排序的数据很大，一次不能容纳全部的排序记录，在排序过程中需要访问外存。

我们这里说说八大排序就是内部排序。

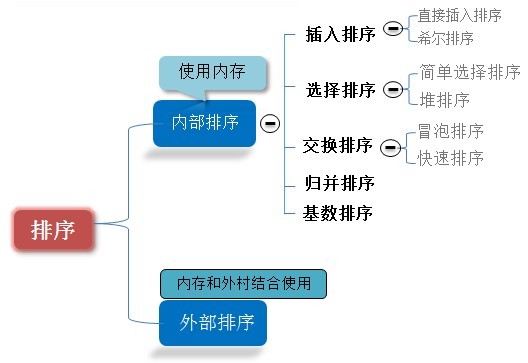
当n较大，则应采用时间复杂度为O(nlog2n)的排序方法：快速排序、堆排序或归并排序序。

快速排序：是目前基于比较的内部排序中被认为是最好的方法，当待排序的关键字是随机分布时，快速排序的平均时间最短；

unsortedList=[55, 91, 63, 71, 72, 7, 74, 16, 4, 31, 100, 51, 94, 35, 49, 46, 43, 59, 18, 17] 

二、算法实现

 

1.插入排序——直接插入排序(Straight Insertion Sort)

基本思想:

将一个记录插入到已排序好的有序表中，从而得到一个新，记录数增1的有序表。即：先将序列的第1个记录看成是一个有序的子序列，然后从第2个记录逐个进行插入，直至整个序列有序为止。

要点：设立哨兵，作为临时存储和判断数组边界之用。

直接插入排序示例：  从后往前插入

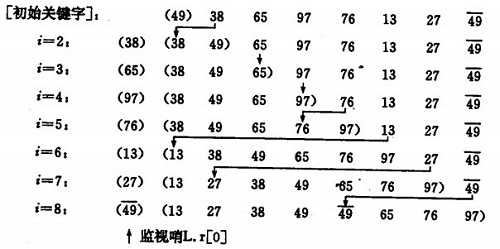
如果碰见一个和插入元素相等的，那么插入元素把想插入的元素放在相等元素的后面。所以，相等元素的前后顺序没有改变，从原无序序列出去的顺序就是排好序后的顺序，所以插入排序是稳定的。

（无哨兵）直接插入排序——算法的实现：

def insertionSort(unsortedList):
    list_length=len(unsortedList)
    if list_length<2:  #这种情况就不用排序了
        return unsortedList
    for i in range(1,list_length):  #所有的数据都要进行排序
        key=unsortedList[i]
        j=i-1
        while j>=0 and key<unsortedList[j]:  #插入排序：如果带排序数字小于当前，则往前移动
            unsortedList[j+1]=unsortedList[j]
            j=j-1
        unsortedList[j+1]=key
    return unsortedList 

如果要实现有哨兵的插入排序算法，就是把第0个元素当做哨兵，本来应该给key的值给数组第0个位置。

两个好处：

1.保存了要插入元素，相当于上边变量key的作用

2.循环的时候不用判断边界，因为判断边界需要浪费时间，所以，有哨兵的会节省时间。

带来的问题：

因为我们通常传进来的数组第0个位置都是有记录的，所以需要把数组往后移动一下， 可以把第一个元素直接放到最后最后的位置。

转自：http://blog.csdn.net/u013719780/article/details/49201143

2.插入排序——希尔排序

基本思想：希尔排序(Shell Sort)是插入排序的一种。也称缩小增量排序，是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。

def shellSort(arrays):
    length=len(arrays)
    if length<2:
        return arrays
    dist=length/2#增量，至少为1
    while (dist>=1):#增量至少为1，即最后一次
        for i in range(1,length):
            key=arrays[i]
            j=i-dist
            while j>=0 and arrays[j]>key:#有增量的插入排序（一定要想明白，这里是插入排序）
                arrays[j+dist]=arrays[j]
                j=j-dist
            arrays[j+dist]=key
        dist=dist/2#增量减小
    return arrays

转自：http://blog.csdn.net/hinyunsin/article/details/6311707

3.选择排序——简单选择排序

算法思想：从未排序的序列中找到一个最小的元素，放到第一位，再从剩余未排序的序列中找到最小的元素，放到第二位，依此类推，直到所有元素都已排序完毕。假设序列元素总共n+1个，则我们需要找n轮，就可以使该序列排好序。

因为交换的原因，可能导致相同大小数字顺序发生改变，所以是不稳定排序。

def selectSort(arrays):
    length=len(arrays)
    if length<2:
        return arrays
    for i in range(length):
        min_index=i#保存最小值的位置
        for j in range(i+1,length):#找最小值
            if arrays[j]<arrays[min_index]:
                min_index=j
        arrays[i],arrays[min_index]=arrays[min_index],arrays[i]#找到最小值，然后让该值和选择排序位置上的数进行交换
    return arrays

4.选择排序——堆排序

算法思想：先建立一个最大堆，在建立最大堆的过程中需要不断调整元素的位置。最大堆建立后，顶端元素必定是最大的元素，把该最大元素与最末尾元素位置置换，最大元素就出现在列表末端。重复此过程，直到排序。

def adjust(arr,start,length):#调整堆
    tmp=arr[start]
    j=2*start+1
    while j<length:
        if j<length-1 and arr[j]<arr[j+1]:
            j+=1
        if tmp>=arr[j]:
            break
        arr[start]=arr[j]
        start=j
        j=2*j+1
    arr[start]=tmp  

def buildHeap(arr): #从一堆乱序中创建一个初始堆
    length=len(arr)
    for i in range(length/2-1,-1,-1):
        adjust(arr,i,length)
def heapSort(arr):  #堆排序
    length=len(arr)
    buildHeap(arr)
    '''''
    建立大根堆后，第一个元素为列表的最大元素，将它跟最后一个元素交换，列表大小-1
    重新调整列表为大根堆，重复此操作直到最后一个元素
    '''
    for i in range(length-1,0,-1):
        arr[i],arr[0]=arr[0],arr[i]
        adjust(arr,0,i)
    return arr

版本2：第一个元素我们不用，这样更好判断孩子节点的位置

def heapSort(arrays):

    length=len(arrays)#length是数据元素个数
    arrays.insert(0,0)#第一个位置插入0，不使用

    buildHeap(arrays)#建立大根堆，array[0]是最大值

    for i in range(length,1,-1):
        arrays[i],arrays[1]=arrays[1],arrays[i]#让第一个元素和最后一个元素交换，把最大值放到最后位置，相当于已经排好序的
        heapAdjust(arrays,1,i-1)#调整剩下的元素

    arrays.pop(0)#把我们强加的第一个元素删掉
    return arrays

def buildHeap(arrays):
    for i in range((len(arrays)-1)/2,0,-1):#因为我们的arrays加了一个0，所以长度要再减去1,第二个参数写0，因为我们array特性，实际上取到1的位置。
                                           #实际上是对(len（arrays）-1)/2……1的元素进行调整
        heapAdjust(arrays,i,len(arrays)-1)

def heapAdjust(arrays, start,length):#start是被调整的元素，length是剩余堆的长度
    temp=arrays[start]#被调整的位置上的元素临时给temp
    for j in range(start*2,length+1):#到孩子节点找比start节点大的元素的位置
        if (j<length and arrays[j]<arrays[j+1]):
            j=j+1
        if(temp>arrays[j]):#如果被调整的位置元素比两个孩子节点都大，不用调整，直接退出
            break
        arrays[start]=arrays[j]#把两个孩子节点中大的值给arrays[start]
        start=j#需要被调整的位置发生变化（变成被调整到父节点的那个节点）

    arrays[start]=temp#把最开始我们的temp（需要被调整的元素值）赋给我们找到的合适的位置

5.交换排序——冒泡排序

冒泡1：从后边开始，和第一个比较，如果比第一个数小，交换，然后一直往前，比较。

def bubbleSort1(lists):
    length = len(lists)
    for i in range(0, length): #i从0开始
        for j in range(i + 1, length): #j从i+1开始
            if lists[i] > lists[j]: #冗余交换，具体参考《大话数据结构》
                lists[i], lists[j] = lists[j], lists[i]
    return lists

冒泡2：从后开始

def bubbleSort2(arrays):#这应该是最常用的版本了
    length=len(arrays)
    for i in range(0,length):
        for j in range(length-1,i,-1):
            if arrays[j]<arrays[j-1]:
                arrays[j],arrays[j-1]=arrays[j-1],arrays[j]
    return arrays

冒泡3：设置标记，如果此次没有交换，说明已经有序了

def bubbleSort3(arrays):
    length=len(arrays)
    flag=True #设置标记
    for i in range(0,length):
        if flag==False: #如果此次没有交换，说明已经排好序了，直接跳出循环
            break
        flag=False
        for j in range(length-1,i,-1):
            if arrays[j]<arrays[j-1]:
                flag=True
                arrays[j],arrays[j-1]=arrays[j-1],arrays[j]
    return arrays
     

6.交换排序——快速排序

算法思想：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

def quickSort(arr): #快排
    if arr==[]:
        return []
    low=0
    high=len(arr)-1
    quickS(arr,low,high)
    return arr

def quickS(arr,low,high): #递归调用
    if low<high:
        pivot=Partition(arr,low,high)

        quickS(arr,low,pivot-1) #和二分查找类似，这里必须有一个进步的阶段，否则会跳不出来循环
        quickS(arr,pivot+1,high)

def Partition(arr,low,high): #找中轴函数
    pivotkey=arr[low]
    while(low<high):
        while(low<high and arr[high]>pivotkey): #因为low那个地方是要覆盖掉的，所以，这里必须要从high开始
            high=high-1
        arr[low],arr[high]=arr[high],arr[low]
        while(low<high and arr[low]<pivotkey):
            low=low+1
        arr[low],arr[high]=arr[high],arr[low]#交换，这也是快速排序归为交换排序的原因
    return low #结束循环的地方就是在low和high相等的地方，就是中轴的位置

改进1：实际上Partition函数的那一部分可以改进，不需要交换

只需要改进Partition函数即可

def Partition(arr,low,high): #找中轴函数
    pivotkey=arr[low]
    while(low<high):
        while(low<high and arr[high]>pivotkey):
            high=high-1
        arr[low]=arr[high]
        while(low<high and arr[low]<pivotkey):
            low=low+1
        arr[high]=arr[low]#交换，这也是快速排序归为交换排序的原因
    arr[low]=pivotkey
    return low #结束循环的地方就是在low和high相等的地方，就是中轴的位置

改进2：当数组非常小的时候，快速排序反而不如直接插入排序的效果好（直接插入排序是简单排序中性能最好的），其原因是快排用到了递归操作。

只需改进quickS函数即可。——有没有写对？不太自信，主要是觉着《大话数据结构上》的写法是错误的。

def quickS(arr,low,high): #递归调用
    if (high-low>5):#假设大于5的时候
        pivot=Partition(arr,low,high)

        quickS(arr,low,pivot-1)
        quickS(arr,pivot+1,high)
    else:
        insertionSort(arr[low:pivot-1])
        insertionSort(arr[pivot+1,high])
            

改进3：如果中轴选择的不合理，会导致快速排序的效率非常的慢，可以从三个数中选择一个中间值，或者九个数中选择一个中间值等。

改进4：把递归改成尾递归方式。

7.归并排序

算法思想：归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

def merge(left, right):#对left和right数组进行合并
    i, j = 0, 0
    result = []
    while i < len(left) and j < len(right):
        if left[i] <= right[j]:
            result.append(left[i])
            i += 1
        else:
            result.append(right[j])
            j += 1
    result += left[i:]
    result += right[j:]
    return result

def mergeSort(lists):
    # 归并排序
    if len(lists) <= 1:
        return lists
    num = len(lists) / 2
    left = mergeSort(lists[:num])#left是数组，存放着数据
    right = mergeSort(lists[num:])
    return merge(left, right)#把left数组和right数组合并

改进：非递归形式。

8.基数排序

算法思想：基数排序（radix sort）属于“分配式排序”（distribution sort），又称“桶子法”（bucket sort）或bin sort，顾名思义，它是透过键值的部份资讯，将要排序的元素分配至某些“桶”中，藉以达到排序的作用，基数排序法是属于稳定性的排序，其时间复杂度为O (nlog(r)m)，其中r为所采取的基数，而m为堆数，在某些时候，基数排序法的效率高于其它的稳定性排序法。

def RadixSort(list,d):
    for k in xrange(d):#d轮排序,即有几位
        s=[[] for i in xrange(10)]#因为每一位数字都是0~9，故建立10个桶
        '''对于数组中的元素，首先按照最低有效数字进行
           排序，然后由低位向高位进行。'''
        for i in list:
            '''对于3个元素的数组[977, 87, 960]，第一轮排序首先按照个位数字相同的
               放在一个桶s[7]=[977],s[7]=[977,87],s[0]=[960]
               执行后list=[960,977,87].第二轮按照十位数，s[6]=[960],s[7]=[977]
               s[8]=[87],执行后list=[960,977,87].第三轮按照百位，s[9]=[960]
               s[9]=[960,977],s[0]=87,执行后list=[87,960,977],结束。'''
            s[i/(10**k)%10].append(i)  #/(10**k)%10是求相应位上的数字
        list=[j for i in s for j in i]
    return list

易错点：多个变量之间的关系，防止变量被修改，比如i,j,k之间，不要产生修改的情况，否则会出错的。

参考：

https://www.liaoxuefeng.com/article/001373888684944cc1e1ec7beca42ccb8b03caf0f879dc1000

https://www.nowcoder.com/profile/9220992/codeBookDetail?submissionId=11240164