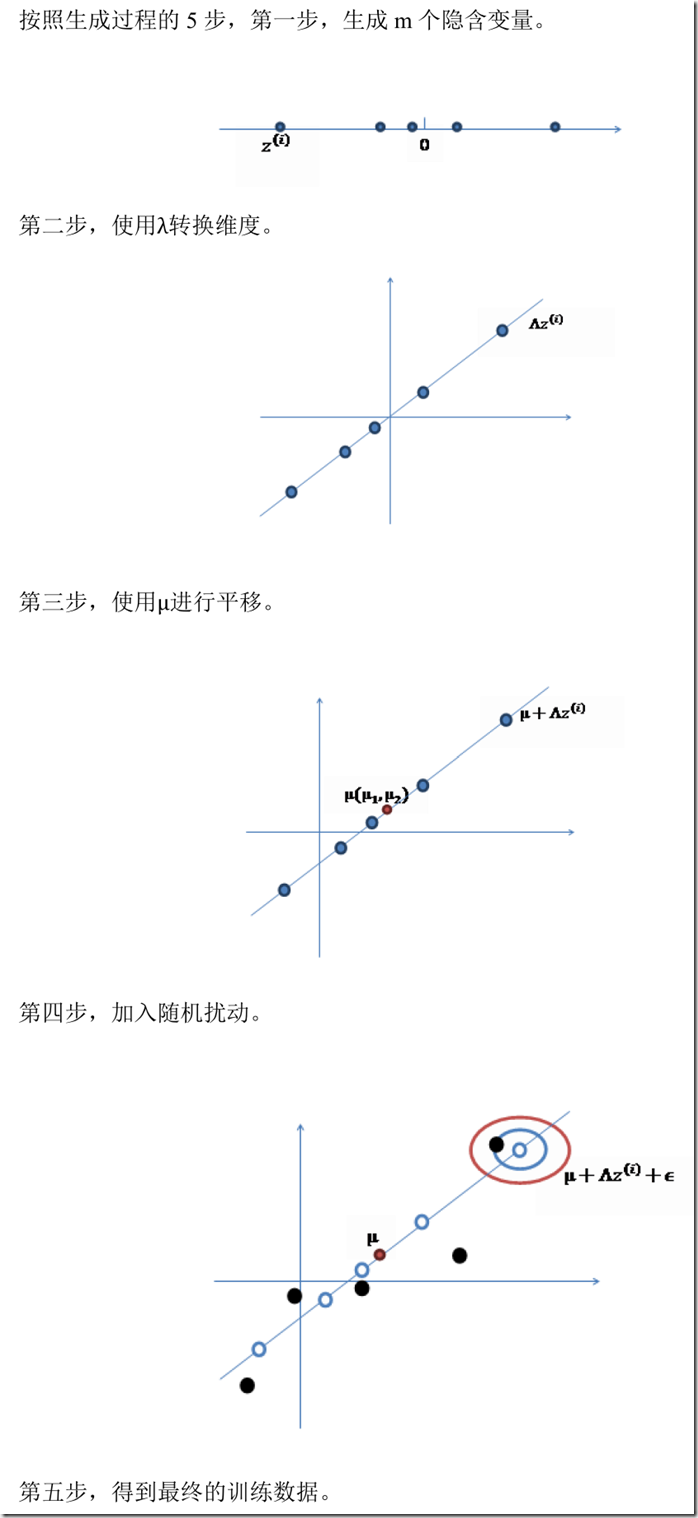
【cs229-Lecture13】高斯混合模型

本节内容：

1、混合高斯模型；

2、将混合高斯模型应用到混合贝叶斯模型；（应用：文本聚类）

3、结合EM算法，讨论因子分析算法；

4、高斯分布的有用性质。

混合高斯模型

将一般化的EM算法流程（下载笔记）应用到混合高斯模型

---

因子分析模型

因子分析的基本目的就是用少数几个因子去描述许多指标或因素之间的联系，即将相关比较密切的几个变量归在同一类中，每一类变量就成为一个因子，以较少的几个因子反映原资料的大部分信息。运用这种研究技术，我们可以方便地找出影响消费者购买、消费以及满意度的主要因素是哪些，以及它们的影响力运用这种研究技术，我们还可以为市场细分做前期分析。

因子分析法的基本思想 
             通过变量的相关系数矩阵内部结构的研究，找出能够控制所有变量的少数几个随机变量的少数几个随机变量去描述多个变量之间的相关关系，但在这里，这少数.几个随机变量是不可观测的，通常称为因子。然后根据相关性的大小把变量分组，只得同组内的变量之间相关性较高，但不同组的变量相关性较低。
因子旋转，在实际应用因子分析中出现了难以解释的现象，根本原因是模型同实际数据的矛盾，而其直接原因表现在因子对变量的贡献不明确。于是设想在不改变因子协方差结构的情况下，通过旋转坐标轴来实现这一目的。
因子分析方法的计算步骤：

第一步：将原始数据标准化。

第二步：建立变量的相关系数R。
              第三步：求R的特征根极其相应的单位特征向量。

第四步：对因子载荷阵施行最大正交旋转。

第五步：计算因子得分。

情景：数据维数>>样本数

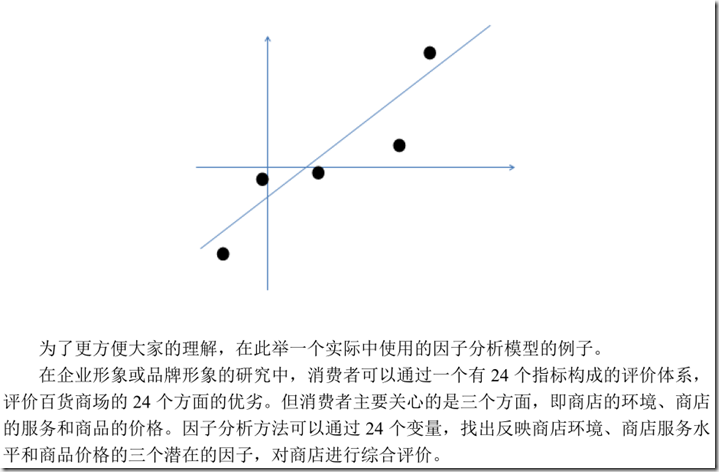
因子分析模型的推导

EM 求解参数