【Python算法】遍历(Traversal)、深度优先(DFS)、广度优先(BFS)

图结构：

　　非常强大的结构化思维（或数学）模型。如果您能用图的处理方式来规范化某个问题，即使这个问题本身看上去并不像个图问题，也能使您离解决问题更进一步。

　　在众多图算法中，我们常会用到一种非常实用的思维模型--遍历（traversal）:对图中所有节点的探索及访问操作。

图的一些相关概念：

　　简单图（Simple graph）：无环并且无平行边的图.

　　路（path）：内部点互不相同的链。

　　如果无向图G中每一对不同的顶点x和y都有一条路，（即W（G）=1，连通分支数）则称G是连通图，反之称为非连通图。

　　两端点相同的路（即闭路）称为圈（cycle）。

　　树（tree）是无圈连通无向图。树中度数为1的结点称为树的叶结点。树中度数大于1的结点称为树的分支节点或内部结点。

　　不相交的若干树称为森林（forest）,即森林的每个连通分支是树。

　　定理1：T是树<=>T中无环，且任何不同两顶点间有且仅有一条路。

　　定理2：T是树<=>T连通且|e|=n-1，|e|为T的边数，n为T的顶点数。

　　由根到某一顶点v的有向路的长度，称为顶点v的层数（level）。根树的高度就是顶点层数的最大值。

深度优先搜索：

　　求连通简单图G的一棵生成树的许多方法中，深度优先搜索（depth first search）是一个十分重要的算法。

基本思想：

　　任意选择图G的一个顶点V₀作为根，通过相继地添加边来形成在顶点V₀开始的路，其中每条新边都与路上的最后一个顶点以及不在路上的一个顶点相关联。

　　继续尽可能多地添加边到这条路。若这条路经过图G的所有顶点，则这条路即为G的一棵生成树；

　　若这条路没有经过G的所有顶点，不妨设形成这条路的顶点顺序V₀,V₁,......,V_n。则返回到路里的次最后顶点V_(n-1).

　　　　若有可能，则形成在顶点v(n-1)开始的经过的还没有放过的顶点的路；

　　　　否则，返回到路里的顶点v(n-2)。

　　然后再试。重复这个过程，在所访问过的最后一个顶点开始，在路上次返回的顶点，只要有可能就形成新的路，直到不能添加更多的边为止。

　　深度优先搜索也称为回溯（back tracking）

栗子：

　　用深度优先搜索来找出图3-9所示图G的生成树，任意地从顶点d开始，生成步骤显示在图3-10。

　　

广度优先搜索：

　　可用广度优先搜索（breadth first search）来产生连通简单图的生成树。

基本思想：

　　从图的顶点中任意第选择一个根，然后添加与这个顶点相关联的所有边，在这个阶段添加的新顶点成为生成树里1层上的顶点，任意地排序它们。

　　下一步，按照顺序访问1层上的每一个顶点，只要不产生回路，就添加与这个顶点相关联的每个边。这样就产生了树里2的上的顶点。遵循同样的原则继续下去，经有限步骤就产生了生成树。

栗子：

　　用广度优先搜索找出图3-9所示图G的生成树，选择顶点f作为根：

　　

两种著名的基本遍历策略：

　　深度优先搜索（depth-first search）

　　广度优先搜索（breadth-first search）

找出图的连通分量：

　　如果一个图中的任何一个节点都有一条路径可以到达其他各个节点，那么它就是连通的。

　　连通分量：目标图中最大（且独立）的连通子图。

　　从图中的某个部分开始，逐步扩大其连通子图的确认范围，直至它再也无法向外连通为止。

def walk(G,s,S=set()):
    P,Q=dict(),set()
    P[s]=None                    # s节点没有前任节点
    Q.add(s)                     # 从s开始搜索
    while Q:
        u=Q.pop()
        for v in G[u].difference(P,S):   # 得到新节点
            Q.add(v)
            P[v]=u               # 记录前任节点
    return P

def components(G):
    comp = []
    seen = set()
    for u in range(9):
        if u in seen: continue
        C = walk(G, u)
        seen.update(C)
        comp.append(C)
    return comp

if __name__ == "__main__":
    a, b, c, d, e, f, g, h, i= range(9)
    N = [
        {b, c, d},   # a
        {a, d},      # b
        {a,d},       # c
        {a,c,d},     # d
        {g,f},       # e
        {e,g},       # f
        {e,f},       # g
        {i},         # h
        {h}          # i
    ]
    comp = components(N)
    print(comp)

深度优先搜索：

　　

　　递归版的深度优先搜索 :

def rec_dfs(G,s,S=None):
    if S is None:S = set()
    S.add(s)
    for u in G[s]:
        if u in S:coontinue
        rec_dfs(G,u,S)

　　迭代版的深度优先搜索 :

def iter_dfs(G,s):
    S,Q=set(),[]
    Q.append(s)
    while Q:
        u = Q.pop()
        if u in S:continue
        S.add(u)
        Q.extend(G[u])
        yield u

if __name__ == "__main__":
    a, b, c, d, e, f, g, h, i = range(9)
    G = [{b, c, d, e, f},  # a
         {c, e},           # b
         {d},              # c
         {e},              # d
         {f},              # e
         {c, g, h},        # f
         {f, h},           # g
         {f, g}            # h
         ]
    print(list(iter_dfs(G,a)))       # [0, 5, 7, 6, 2, 3, 4, 1]

　　通用性的图遍历函数

def traverse(G,s,qtype=set()):
    S,Q=set(),qtype()
    Q.add(s)
    while Q:
        u=Q.pop()
        if u in S:continue
        S.add(u)
        for v in G[u]:
            Q.add(v)
        yield u  

class stack(list):
    add=list.append  

g=list(traverse(G,0,stack))  

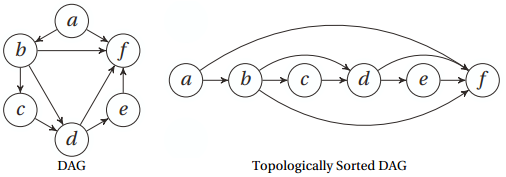
基于深度优先搜索的拓扑排序

　　

def dfs_topsort(G):
    S,res=set(),[]
    def recurse(u):
        if u in S: return
        S.add(u)
        for v in G[u]:
            recurse(v)
        res.append(u)
    for u in G:
        recurse(u)
    res.reverse()
    return res

if __name__=="__main__":
    a, b, c, d, e, f, g, h, i = range(9)
    G = {
        'a': set('bf'),
        'b': set('cdf'),
        'c': set('d'),
        'd': set('ef'),
        'e': set('f'),
        'f': set('')
    }
    res = dfs_topsort(G)

迭代深度的深度优先搜索

def iddfs(G,s):
    yielded=set()
    def recurse(G,s,d,S=None):
        if s not in yielded:
            yield s
            yielded.add(s)
        if d==0:return
        if S is None:S=set()
        S.add(s)
        for u in G[s]:
            if u in S:continue
            for v in recurse(G,u,d-1,S):
                yield v
    n=len(G)
    for d in range(n):
        if len(yielded)==n:break
        for u in recurse(G,s,d):
            yield u  

if __name__=="__main__":
    a, b, c, d, e, f, g, h, i= range(9)
    N = [
        {b, c, d},  # a
        {a, d},     # b
        {a,d},      # c
        {a,b,c},    # d
        {g,f},      # e
        {e,g},      # f
        {e,f},      # g
        {i},        # h
        {h}         # i
    ]  

    G = [{b,c,d,e,f},#a
        {c,e},      # b
        {d},        # c
        {e},        # d
        {f},        # e
        {c,g,h},    # f
        {f,h},      # g
        {f,g}       # h
   ]  

    p=list(iddfs(G,0))         # [0, 1, 2, 3, 4, 5, 6, 7]
    m=list(iddfs(N,0))         # [0, 1, 2, 3]  

广度优先搜索

import collections
def bfs(G,s):
    P,Q={s:None},collections.deque([s])
    while Q:
        u=Q.popleft()
        for v in G[u]:
            if v in P:continue
            P[v]=u
            Q.append(v)
    return P  

强连通分量

　　如果有向图的任何一对结点间是相互可达的，则称这个有向图是强连通的

def tr(G):
    GT={}
    for u in G:GT[u]=set()
    for u in G:
        for v in G[u]:
            GT[v].add(u)
    return GT
def scc(G):
    GT=tr(G)
    sccs,seen=[],set()
    for u in dfs_topsort(G):
        if u in seen:continue
        C=walk(GT,u,seen)
        seen.update(C)
        sccs.append(C)
    return sccs  

def dfs_topsort(G):
    S,res=set(),[]
    def recurse(u):
        if u in S:return
        S.add(u)
        for v in G[u]:
            recurse(v)
        res.append(u)
    for u in G:
        recurse(u)
    res.reverse()
    return res  

def walk(G,s,S=set()):
    P,Q=dict(),set()
    P[s]=None
    Q.add(s)
    while Q:
        u=Q.pop()
        print("u: ",u)
        print("S:",S)
        for v in G[u].difference(P,S):
            Q.add(v)
            P[v]=u
    return P  

if __name__=="__main__":
    a, b, c, d, e, f, g, h, i= range(9)  

    G={
        'a':set('bc'),
        'b':set('edi'),
        'c':set('d'),
        'd':set('ah'),
        'e':set('f'),
        'f':set('g'),
        'g':set('eh'),
        'h':set('i'),
        'i':set('h')
        }
    sccs=scc(G)
    # [{'a': None, 'd': 'a', 'c': 'd', 'b': 'd'}, {'e': None, 'g': 'e', 'f': 'g'}, {'h': None, 'i': 'h'}]