Andorid 翻书效果

本文内容

• 项目结构
• 环境
• 演示
• 参考资料

翻书效果，主要采用绘制贝塞尔曲线的方法。本文有三个演示：

• 简单翻书效果。翻下一页后，当前页不会消失。
• 翻书时的贝塞尔曲线。演示翻书时，贝塞尔曲线的路径和要素。
• 完整翻书效果。

下载 Demo

（运行源代码，请先将压缩包内 test.txt 文件复制到 SD 卡根目录）

项目结构

---

图 1 项目结构                                                                   图 2 程序主界面

环境

---

• Windows 2008 R2 64 位
• Eclipse ADT V22.6.2，Android 4.4.2（API 19）
• SAMSUNG GT-8618，3.5英寸屏（7.5x5 cm，苹果一样），Android OS 4.1.2

演示

---

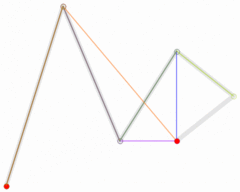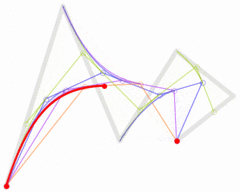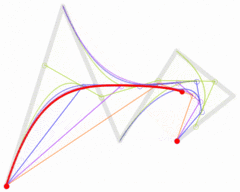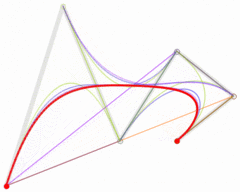
实现翻书效果，就是对当前页和下一页的剪切、组合过程。如图 3 所示，可以看到3个部分：当前页的可见部分（绿色部分）；当前页的不可见部分（黄色部分），即当前也的背面；下一页（蓝色部分）。

如果你不了解贝赛尔曲线，先查点资料单独体会一下贝塞尔曲线，也不用太仔细。本例是从触摸屏幕的那个点开始，确定绘制贝塞尔曲线的各个要素，基本都是数学问题。最后，加上效果。

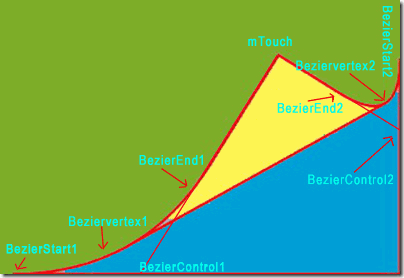
图 3 程序中各个点的标识

需要注意的地方：

1，翻书时，页背面有两部分处理，一是将原图翻转，利用Matrix mMatrix和float[] mMatrixArray 实现，而是，原图翻转后的光影效果，需要使用 ColorMatrixFilter。

2，书边缘的阴影部分。

图 4 简单翻书效果（左：当前书页；中：翻下一页；右：翻上一页）

图 5 翻书时的贝塞尔曲线（左：当前书页；中：翻下一页；右：翻上一页）

在图 5 你可以看到，贝塞尔曲线的各个区域和要素。

图 6 翻书完整效果（第一个：当前书页；第二个：翻下一页；第三个：翻下一页时消失，出现书第二页；第四个：翻上一页）

贝塞尔曲线

数值分析领域中，贝塞尔曲线（Bézier curve）是电脑图形学中相当重要的参数曲线。更高维度的广泛化贝塞尔曲线就称作贝塞尔曲面，其中贝塞尔三角是一种特殊的实例。

贝塞尔曲线于1962年，由法国工程师皮埃尔·贝塞尔（Pierre Bézier）所广泛发表，他运用贝塞尔曲线来为汽车的主体进行设计。贝塞尔曲线最初由Paul de Casteljau于1959年运用de Casteljau算法开发，以稳定数值的方法求出贝塞尔曲线。

• 线性贝塞尔曲线

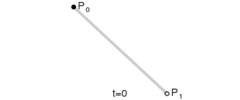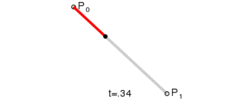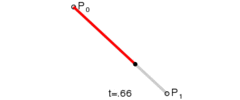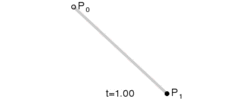
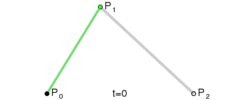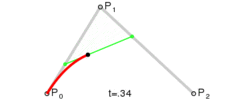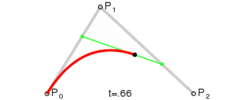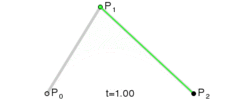
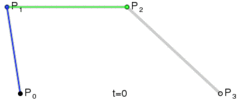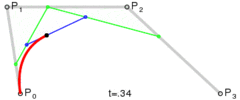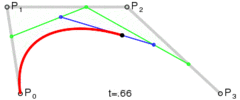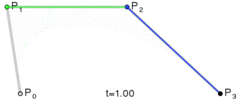
其路径由给定点 P₀、P₁，线性贝塞尔曲线只是两点之间的一条直线。其贝塞尔曲线 B(t)：

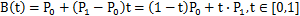
线性贝塞尔曲线演示动画，t 在 [0,1] 区间

因此，线性贝塞尔曲线等同于线性插值。

• 二次方贝塞尔曲线

其路径由给定点 P₀、P₁、P₂，其贝塞尔曲线 B(t)：

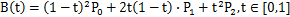
二次贝塞尔曲线演示动画，t 在 [0,1] 区间

TrueType 字型就运用了以贝塞尔样条组成的二次贝塞尔曲线。

• 三次方贝塞尔曲线

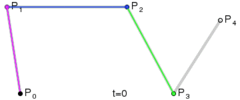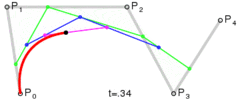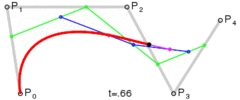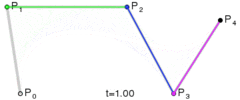
P₀、P₁、P₂、P₃ 四个点在平面或在三维空间中定义了三次方贝塞尔曲线。曲线起始于 P₀ 走向 P₁，并从 P₂ 的方向来到 P₃。一般不会经过 P₁ 或 P₂；这两个点只是在那里提供方向资讯。P₀ 和 P₁ 之间的间距，决定了曲线在转而趋进 P₃ 之前，走向 P₂ 方向的“长度有多长”。其贝塞尔曲线 B(t)：

三次贝塞尔曲线演示动画，t 在 [0,1] 区间

现代的成像系统，如 PostScript、Asymptote和Metafont，运用了以贝塞尔样条组成的三次贝塞尔曲线，用来描绘曲线轮廓。

四次、五次贝塞尔曲线演示动画，t 在 [0,1] 区间

• 一般化

n 阶贝塞尔曲线可做如下推断。给定点 P₀、P₁、…、P_n，其贝塞尔曲线 B(t)：

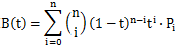
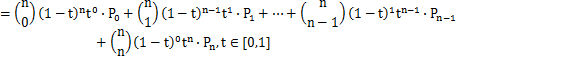
假设 n=5，则

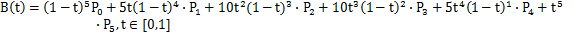
上面公式可用递归表达。

用 表示由点 P₀、P₁、…、P_n 所决定的贝塞尔曲线。则，

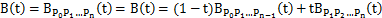
换句话说，n 阶的贝塞尔曲线，即双n-1 阶贝塞尔曲线之间的插值。

参考资料

---

• Wiki 贝塞尔曲线
• 另一个博文如何计算各个要素的方法

下载 Demo