「Luogu 1471」 方差

---

题目背景

滚粗了的HansBug在收拾旧数学书，然而他发现了什么奇妙的东西。

题目描述

蒟蒻HansBug在一本数学书里面发现了一个神奇的数列，包含N个实数。他想算算这个数列的平均数和方差。

输入输出格式

输入格式：

第一行包含两个正整数N、M，分别表示数列中实数的个数和操作的个数。

第二行包含N个实数，其中第i个实数表示数列的第i项。

接下来M行，每行为一条操作，格式为以下两种之一：

操作13：1 x y k ，表示将第x到第y项每项加上k，k为一实数。

操作2：2 x y ，表示求出第x到第y项这一子数列的平均数。

操作3：3 x y ，表示求出第x到第y项这一子数列的方差。

输出格式：

输出包含若干行，每行为一个实数，即依次为每一次操作2或操作3所得的结果（所有结果四舍五入保留4位小数）。

输入输出样例

输入样例：                                                                  输出样例

5 5                                                                              3.0000

1 5 4 2 3                                                                      2.0000

2 1 4                                                                            0.8000

3 1 5

1 1 1 1

1 2 2 -1

3 1 5

说明

数据范围

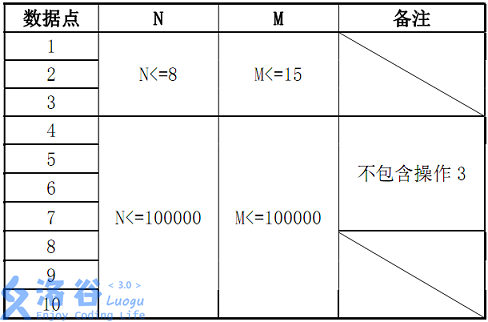
-------------------------------------分界线-------------------------------------

题解

这道题要求两个值，一个是平均值，一个是方差，平均值很容易，就是区间和/个数就可以了。但是怎么求方差呢？看上去十分困难,不知道如何下手,不知道怎么维护？但是不妨把方差的公式拆开：

    设平均数为k

    则S²=[(a1-k)²+(a2-k)²+(a3-k)²+...+(an-k)²]/n(将他拆开)

           =[a1²+a2²+a3²+...+an²+nk²-2k(a1+a2+a3+...+an)]/n

    ∵ (a1+a2+a3+...+an)/n=k

    ∴ S²=(a1²+a2²+a3²+...+an²)/n-k²

    所以现在显而易见要维护方差只要维护平方的和就可以了

    那么怎么维护平方和呢？

    在拆开一下：

        设每个数加上了x

         (a1+x)²+(a2+x)²+(a3+x)²+...+(an+x)²

         =a1²+a2²+a3²+...+an²+nx²+2x(a1+a2+a3+...+an)

    所以现在就很容易了，接下来上代码

#include<cstdio>
#include<cstdlib>
#include<iostream>
using namespace std;
struct node {
    double lazy,v,sqr;
} a[400001];
double b[400001];
void pushup(int k) {
    a[k].v=a[k<<1].v+a[k<<1|1].v;
    a[k].sqr=a[k<<1].sqr+a[k<<1|1].sqr;
}
void add(int k,int l,int r,double v) {
    a[k].lazy+=v;
    a[k].sqr+=((r-l+1)*v*v+2*v*a[k].v);
    a[k].v+=(r-l+1)*v;
}
void pushdown(int k,int l,int r) {
    if(a[k].lazy) {
        int mid=(l+r)>>1;
        add(k<<1,l,mid,a[k].lazy);
        add(k<<1|1,mid+1,r,a[k].lazy);
    }
    a[k].lazy=0;
}
void update(int k,int l,int r,int begin,int end,double c) {
    if(r<begin||l>end)
        return ;
    if(l>=begin&&r<=end) {
        add(k,l,r,c);
        return;
    }
    pushdown(k,l,r);
    int mid=(l+r)>>1;
    update(k<<1,l,mid,begin,end,c);
    update(k<<1|1,mid+1,r,begin,end,c);
    pushup(k);
}
double find(int k,int l,int r,int begin,int end) {
    if(r<begin||l>end)
        return 0;
    if(l>=begin&&r<=end)
        return a[k].v;
    pushdown(k,l,r);
    int mid=(l+r)>>1;
    if(end<=mid)
        return find(k<<1,l,mid,begin,end);
    else if(begin>mid)
        return find(k<<1|1,mid+1,r,begin,end);
    else
        return find(k<<1,l,mid,begin,mid)+find(k<<1|1,mid+1,r,mid+1,end);
}
double find1(int k,int l,int r,int begin,int end) {
    if(r<begin||l>end)
        return 0;
    if(l>=begin&&r<=end)
        return a[k].sqr;
    pushdown(k,l,r);
    int mid=(l+r)>>1;
    if(end<=mid)
        return find1(k<<1,l,mid,begin,end);
    else if(begin>mid)
        return find1(k<<1|1,mid+1,r,begin,end);
    else
        return find1(k<<1,l,mid,begin,mid)+find1(k<<1|1,mid+1,r,mid+1,end);
}
void build(int k,int l,int r) {
    a[k].lazy=0;
    if(l==r) {
        a[k].v=b[l];
        a[k].sqr=b[l]*b[l];
        return ;
    }
    int mid=(l+r)>>1;
    build(k<<1,l,mid);
    build(k<<1|1,mid+1,r);
    pushup(k);
}
int main() {
    int n,m,L,x,y;
    double c;
    scanf("%d%d",&n,&m);
    for(int i=1; i<=n; i++)
        scanf("%lf",&b[i]);
    build(1,1,n);
    for(int i=1; i<=m; i++) {
        scanf("%d%d%d",&L,&x,&y);
        if(L==1) {
            scanf("%lf",&c);
            update(1,1,n,x,y,c);
        }
        if(L==2)
            printf("%0.4lf\n",find(1,1,n,x,y)*1.0/(y-x+1));
        if(L==3) {
            double ans=find(1,1,n,x,y)*1.0/(y-x+1);
            ans*=ans;
            printf("%0.4lf\n",(find1(1,1,n,x,y)*1.0/(y-x+1))-ans);
        }
    }
}